WHU 1540 Fibonacci 递推

武大邀请赛的网络预选赛，就去做了个签到题，居然连这个递推都没推出来，真是惭愧。

而且好久没写矩阵乘法了，来回顾一下。

题意：

　　求Fibonacci数列的，前n项立方和。

思路：

　　可以求得一下递推公式：

 

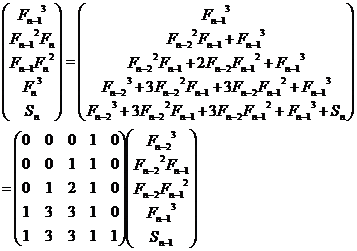
然后用矩阵快速幂求出结果即可。

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <functional>

using namespace std;

typedef long long ll;

const ll MOD  = (ll)1e9+7;
const ll ONE[][5] = {
    {1, 0, 0, 0, 0},
    {0, 1, 0, 0, 0},
    {0, 0, 1, 0, 0},
    {0, 0, 0, 1, 0},
    {0, 0, 0, 0, 1},
};
const ll MU[][5] = {
    {0, 0, 0, 1, 0},
    {0, 0, 1, 1, 0},
    {0, 1, 2, 1, 0},
    {1, 3, 3, 1, 0},
    {1, 3, 3, 1, 1},
};
const ll v1[5] = {1, 1, 1, 1, 2};
struct Matrix {
    ll body[5][5];

    Matrix() {}
    Matrix(bool x) {
        if (x) {
            for (int i = 0; i < 5; i++)
                for (int j = 0; j < 5; j++)
                    body[i][j] = ONE[i][j];
        } else {
            for (int i = 0; i < 5; i++)
                for (int j = 0; j < 5; j++)
                    body[i][j] = MU[i][j];
        }
    }

    Matrix operator * (const Matrix &x) {
        Matrix res;
        ll tmp = 0;
        for (int i = 0; i < 5; i++)
            for (int j = 0; j < 5; j++) {
                tmp = 0;
                for (int k = 0; k < 5; k++)
                    tmp = (tmp+(body[i][k]*x.body[k][j])%MOD)%MOD;
                res.body[i][j] = tmp;
            }
        return res;
    }
};

Matrix pow(int k){
    Matrix res(true);
    Matrix d(false);
    while (k>0) {
        if (k&1) res = res*d;
        d = d*d;
        k >>= 1;
    }
    return res;
}

int n;
ll v2[5];

int main() {
    #ifdef Phantom01
        freopen("WHU1540.txt", "r", stdin);
    #endif // Phantom01

    while (scanf("%d", &n)!=EOF) {
        if (0==n) break;

        if (n<=2) {
            printf("%d
", n);
            continue;
        }
        Matrix tmp = pow(n-2);
        ll t = 0;
        for (int i = 0; i < 5; i++) {
            t = 0;
            for (int j = 0; j < 5; j++)
                t = (t+(tmp.body[i][j]*v1[j])%MOD)%MOD;
            v2[i] = t;
        }
        printf("%d
", (int)v2[4]);
    }

    return 0;
}