
#include<cstdio> #include<iostream> #include<cstring> using namespace std; struct edge{ int next,to; edge(){ } edge(int a,int b){ next=a; to=b; } }E[10004];//建一个图…… int f[100001][31],dep[100001],first[100001],tot; int n,m,root; void add_to_edge(int x,int y) { E[++t]=edge(first[x],y); first[x]=t; }//连边(无向图连两次哦) void dfs(int x,int fa) { f[x][0]=fa; dep[x]=dep[fa]+1; //初始化 , 它的深度是它父亲的深度+1,x 往上倍增 2^0 层 是它的父亲 int k=ceil(log(dep[x])/log(2));//倍增上限 for (int i=1; i<=k; i++) { f[x][i]=f[f[x][i-1]][i-1]; }//f数组存预处理的值,f[x][i]存的是x向上倍增 for (int i=first[x]; i; i=E[i].next) { int pos=E[i].to; if (pos!=fa)//防止死循环,由于是存了两次所以E[i].to会连向它的父亲 dfs(pos,x); } }//预处理 int n,m,root; void LCA() { if (dep[x]<dep[y]) swap(x,y); int k1=dep[x]-dep[y]; int k2=ceil((log(n))/log(2)); for (int i=0; i<=k2; i++) { if (k1&(1<<i)) x=fa[x][i]; }//向上跳!! if (x==y) return x;//两者在同一层并且相等那么x 就是它们的共同祖先 int k3=(log(dep[x])/log(2)); for (int i=k3; i>=0; i--) { if (f[x][i]!=f[y][i]) { x=f[x][i]; y=f[y][i]; }//倍增 } return f[x][0]; } int main() { cin>>n>>m>>root; for (int i=1; i<=m; i++) { int x,y; cin>>x>>y; add_to_edge(x,y); add_to_edge(y,s); } dfs(root,0); }
还是济南集训的内容,让人头秃(不得不说两个老师讲了两遍我勉勉强强才搞懂一点点)
首先来看:
LCA的含义
Least Common Ancestors
LCA就是最近公共祖先,至于它的含义,我觉得例题写的看起来会更清楚,请看:
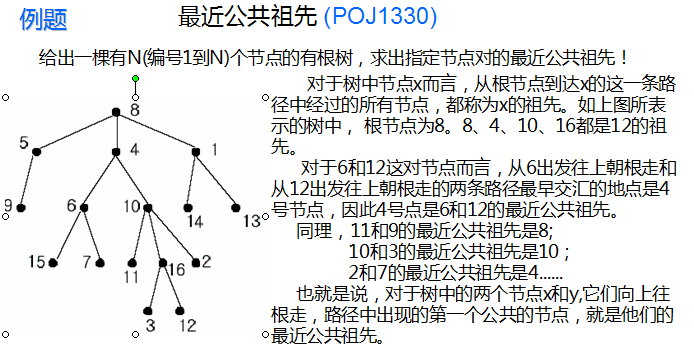
好的,明白了它的含义后,我们很容易想到朴素算法:
询问(x,y)的最近公共祖先,可以先向上枚举x的所有祖先,保存在数组Anc[]中。然后以相同的方法向上枚举y的所有祖先,当第一次发现有y的某个祖先k出现在Anc[]中,则输出k,算法结束。
此时,每次查询复杂度为O( N )
(TLE警告哦)
那么其他方法呢,请看,这里介绍两种,树上倍增,与树链剖分(会在下一篇博客里写到)
树上倍增算法
核心思想:
- 令F[x][n]表示x的2^n级祖先是谁.
- 所以:F[x][n] = F[F[x][n – 1]][n – 1].
- 对于两个点x, y.,求他们的LCA
- 先把x, y提到同一高度.(方便向上进行倍增)
- N从大到小枚举.(从高往低跳)
- 查询F[x][n], F[y][n]是不是相等(比较倍增后的祖先,防止误判)
- 如果是的话说明n太大了,把n改小点.(最近公共祖先的祖先一定是他们的共同祖先)
- 不是的话就说明n不大,可以把x, y上移.(这个很容易理解吧)
原理,如下图(图片来自老师的ppt)(它其实应该有个动图然而我不知道动图怎么传):
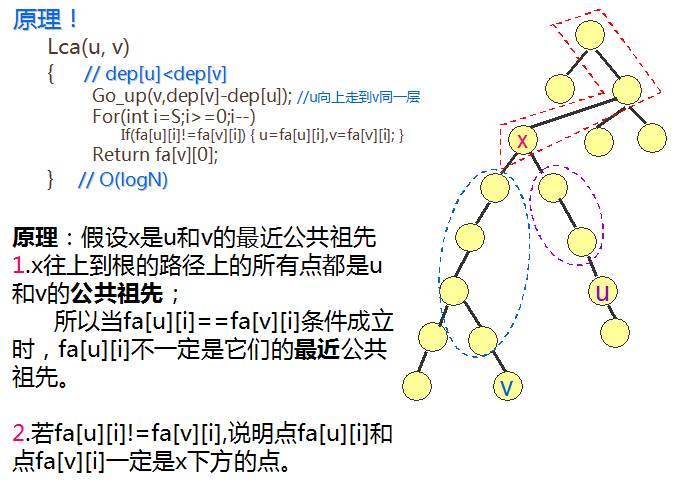
看明白思路了吗,思路还是可以懂得吧,那我们来看代码,理解代码基本就能写了!
(不过我之前也始终看不明白代码就是了,思路都懂代码不会打,我可真是个小垃圾哦)

#include<cstdio> #include<iostream> #include<cmath> using namespace std; const int maxn = 500005; const int maxe = 1000005; int n,m,root; struct line { int from,to; line(){}//空构造函数 line p; line(int A,int B){ //构造函数 line L=line(1,2); from=A;to=B; } }edge[maxe]; //上面是新建一个树 int last[maxn],_next[maxe],e; //last[x]表示以x为起点的最后一条边(的编号) //_next[i]表示与第i条边起点相同的上一条边(的编号) void add_edge(int x,int y) { edge[++e]=line(x,y); _next[e]=last[x]; last[x]=e; } //存边 int Fa[maxn][35],Dep[maxn]; void dfs(int x,int fa) { int i,k,y; Fa[x][0]=fa;//当前节点x的父亲节点fa Dep[x]=Dep[Fa[x][0]]+1; //x的深度是它父亲节点的深度+1 //记录当前节点的深度 k=ceil(log(Dep[x])/log(2)); //ceil函数是向上取整 //x往上倍增的上限 for(i=1;i<=k;i++)Fa[x][i]=Fa[Fa[x][i-1]][i-1]; //倍增计算祖先 ,记录 for(int i=last[x];i;i=_next[i])//枚举与x相邻的边 { int v=edge[i].to; if(v!=fa)dfs(v,x); } } int LCA(int x,int y) { int i,k,s; s=ceil(log(n)/log(2)); //该树倍增最大可能的上限 if(Dep[x]<Dep[y])swap(x,y); //交换x和y的值 /////////////x往上走k层,让x与y处于同一层 ////////// k=Dep[x]-Dep[y]; for(i=0;i<=s;i++) if(k&(1<<i))x=Fa[x][i]; if(x==y)return x; //x==y时,x就是最近公共祖先 /////////////////////////////////////////////////// s=ceil(log(Dep[x])/log(2)); //计算向上倍增的上限 for(i=s;i>=0;i--) if(Fa[x][i]!=Fa[y][i]){ x=Fa[x][i]; y=Fa[y][i]; } return Fa[x][0]; } int main() { int i,j,k; cin>>n>>m>>root; for(i=1;i<n;i++) { int x,y; scanf("%d%d",&x,&y); add_edge(x,y); add_edge(y,x);//它是树,也就是无向图,所以存两次边 } dfs(root,0);//预处理 for(i=1;i<=m;i++) { int x,y; scanf("%d%d",&x,&y); printf("%d ",LCA(x,y)); } }
OK吗?
这里建议去练练板子,指路-> https://www.luogu.org/problem/P3379
(哇我居然可以写蓝题了哎!!可喜可贺)
先到这里,如有问题欢迎指正
