快速排序法
快速排序算法两个核心点,分别为 “哨兵划分” 和 “递归” 。有点像二分法
- 哨兵划分操作: 以数组某个元素(常常选取首元素)为 基准数key,called 哨兵 ,将所有小于哨兵的元素移动至哨兵的左边,大于哨兵的元素移动至哨兵的右边。
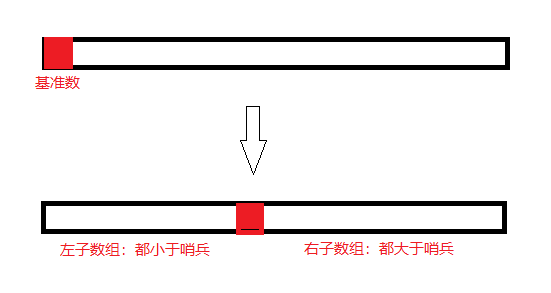
- 递归操作:对 左子数组 和 右子数组 递归执行 “哨兵划分操作”,直至子数组长度为 1 时终止递归,即可完成对整个数组的排序。
复杂度分析:
时间复杂度 O(N log N): 库函数sorted(arr) arr.sort()、快排等排序算法的平均时间复杂度为O(NlogN) 。
空间复杂度 O(N)O(N) : 快速排序的递归深度最好(平均)为 O(logN) ,最差情况(即输入数组完全倒序)为O(N)。
void quickSort(vector<int>& arr,int l, int r){ //当子数字长度为1时终止 if(l>=r) return; //选取第一个元素arr[1]作为哨兵 做“哨兵划分操作” int i=l,j=r; while(i<j){ while(arr[j]>=arr[l] && i<j) j--; while(arr[i]<=arr[l] && i<j) i++; swap(arr[i],arr[j]); } swap(arr[i],arr[l]); // 递归操作 分别对 左子数组 和 右子数组 quickSort(arr,l,i-1); quickSort(arr,i+1,r); }

def quickSort(arr,l,r): if l>=r: return i,j = l,r while i<j: while i<j and arr[j] >= arr[l]: j-=1 while i<j and arr[i] <= arr[l]: i+=1 arr[i],arr[j] = arr[j],arr[i] arr[i],arr[l] = arr[l],arr[i] quickSort(arr,l,i-1) quickSort(arr,i+1,r) quickSort(arr,0,len(arr)-1)

图片来自:https://www.cnblogs.com/l199616j/p/10597245.html (快排)
P.S. 根据不同的顺序要求,可以将顺序代码更改(但内核其实还是一样的:哨兵+递归),应用在不同的场景中,举个栗子:
class SolutionOfminNumber { public: //https://leetcode-cn.com/problems/ba-shu-zu-pai-cheng-zui-xiao-de-shu-lcof/ // 这题本质上是排序题 要求的顺序是整个拼接起来的字符串最小 内核就是 任意两个数a, b 若a + b > b + a 则 b->a 否则 a->b // 套用任何排序方法就可以 最后再做一次字符串拼接 string minNumber(vector<int>& nums) { vector<string> strs; string res = ""; for (int i = 0; i < nums.size(); i++) { strs.push_back(to_string(nums[i])); } quick_sort(0, strs.size() - 1, strs); for (int i = 0; i < strs.size(); i++) { res += strs[i]; } return res; } void quick_sort(int left, int right, vector<string>& strs) { if (left >= right) return; int i = left; int j = right; while (i < j) { while (strs[j] + strs[left] >= strs[left] + strs[j] && i < j) j -= 1; while (strs[i] + strs[left] <= strs[left] + strs[i] && i < j) i += 1; string temp = strs[i]; strs[i] = strs[j]; strs[j] = temp; } string temp = strs[i]; strs[i] = strs[left]; strs[left] = temp; quick_sort(left, i - 1, strs); quick_sort(i + 1, right, strs); } /* solution in python def minNumber(self, nums: List[int]) -> str: def quick_sort(left,right): if left >= right:return #停止的标志 i,j = left,right while i<j: #这步要重复 直到i==j while strs[j]+strs[left]>=strs[left]+strs[j] and i<j:j-=1 while strs[i]+strs[left]<=strs[left]+strs[i] and i<j:i+=1 strs[i],strs[j]=strs[j],strs[i] strs[i],strs[left]=strs[left],strs[i] quick_sort(left,i-1) quick_sort(i+1,right) strs = [str(num) for num in nums] quick_sort(0,len(strs) -1) return ''.join(strs) */ /* 快速排序C语言 void sort(int *a, int left, int right) { if(left >= right)//如果左边索引大于或者等于右边的索引就代表已经整理完成一个组了{ return ; } int i = left; int j = right; int key = a[left]; while(i < j) //控制在当组内寻找一遍 { while(i < j && key <= a[j]) //而寻找结束的条件就是,1,找到一个小于或者大于key的数(大于或小于取决于你想升 //序还是降序)2,没有符合条件1的,并且i与j的大小没有反转 { j--;//向前寻找 } swap(a,i,j);//交换a[i]和a[j]的数值 //找到一个这样的数后就把它赋给前面的被拿走的i的值(如果第一次循环且key是a[left],那么就是给key) while(i < j && key >= a[i])//这是i在当组内向前寻找,同上,不过注意与key的大小关系停止循环和上面相反,因为排序思想是把数往两边扔,所以左右两边的数大小与key的关系相反 { i++; } swap(a,i,j); } sort(a, left, i - 1);//最后用同样的方式对分出来的左边的小组进行同上的做法 sort(a, i + 1, right);//用同样的方式对分出来的右边的小组进行同上的做法 //当然最后可能会出现很多分左右,直到每一组的i = j 为止 } */ };
Top-K问题快排解法
class Solution { public: //https://leetcode-cn.com/problems/zui-xiao-de-kge-shu-lcof/ //返回数组的前k大 vector<int> getLeastNumbers(vector<int>& arr, int k) { quickSort(arr,0,arr.size()-1); vector<int> res; //返回排序后的arr的前k个元素的vector 截取vector res.assign(arr.begin(),arr.begin()+k); return res; } void quickSort(vector<int>& arr,int l, int r){ //当子数字长度为1时终止 if(l>=r) return; //选取第一个元素arr[1]作为哨兵 做“哨兵划分操作” int i=l,j=r; while(i<j){ while(arr[j]>=arr[l] && i<j) j--; while(arr[i]<=arr[l] && i<j) i++; swap(arr[i],arr[j]); } swap(arr[i],arr[l]); // 递归操作 分别对 左子数组 和 右子数组 quickSort(arr,l,i-1); quickSort(arr,i+1,r); } };
