题目
URL:https://leetcode.com/problems/median-of-two-sorted-arrays/
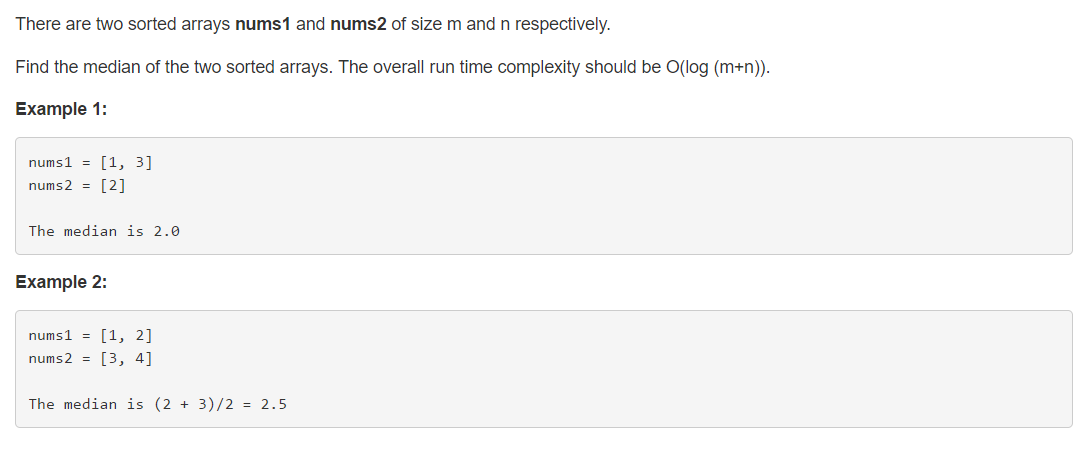
解法
二分法。
总的思想是将 2 个数组用 2 个指针“整体”二分。具体来说,调整 2 个二分指针的位置,达到:
- 左半部分 size = 右半部分 size (2 个数组大小和为奇数可以相差 1)
- 划分左面的数值 < 划分右面的数值,由于两个数组都为有序数组,只需要保证划分边界的值左下角小于右上角以及左上角小于右下角。
在这个过程中,注意:
- 划分数组的长度,通常后一个数组长,方便处理。
- 注意划分边界,到了划分边界,说明划分已完成(不能再划分了),接下来只需要处理值。
划分完成后取划分值,注意划分取值:
- 若划分左面值不存在,忽略即可。
- 奇数,只需要去划分左面的最大值。
- 偶数,取划分左面最大值和划分右面最小值。
public double findMedianSortedArrays(int[] nums1, int[] nums2) { if (nums1.length > nums2.length) return findMedianSortedArrays(nums2, nums1); int imin = 0, imax = nums1.length, i = 0, j = 0; while (imin <= imax) { i = (imin + imax) / 2; j = (nums1.length + nums2.length + 1) / 2 - i; if (i > 0 && nums1[i - 1] > nums2[j]) { imax = i - 1; } else if (i < nums1.length && nums1[i] < nums2[j - 1]) { imin = i + 1; } else { break; } } int maxLeft; if (i == 0) { maxLeft = nums2[j - 1]; } else if (j == 0) { maxLeft = nums1[i - 1]; } else { maxLeft = Math.max(nums1[i - 1], nums2[j - 1]); } if ((nums1.length + nums2.length) % 2 != 0) return maxLeft; int maxRight; if (i == nums1.length) { maxRight = nums2[j]; } else if (j == nums2.length) { maxRight = nums1[i]; } else { maxRight = Math.min(nums1[i], nums2[j]); } return (double) (maxLeft + maxRight) / 2; }
二分法,时间复杂度O(log2(m+n)),运行时间约为 70 ms。
总结
很难很经典,对于二分查找领域来说,又产生了一个新的高度:不再是一个数组的二分查找,而是多个数组的二分查找。