一.线段树的相关定义及用途
(1)线段树的定义
线段树是一种可以加快对区间进行更新以及查询的一种树状结构,类似于将一个区间的及其子区间的相关信息存储在一颗二叉树中。
(2)线段树的用途大致为以下几种
1>某个子区间进行区间更新
2>查询某个子区间的总和
3>查询某个子区间的最值
二.线段树的建立
(1)节点的内容(一个节点代表一个区间)
1>NodeLeft-----该区间的左边界
2>NodeRight-----该区间的右边界
3>NodeMin--------该区间的最小值
4>NodeMax------该区间的最大值
5>NodeSum------该区间的总和
(2)利用节点之间的下标表示它们所代表的区间之间的关系
1>设父节点的编号为n,则其左半区间的编号为2*n,右半区间的编号为2*n+1
2>设某个非总区间的编号为n,则其父区间编号为n/2
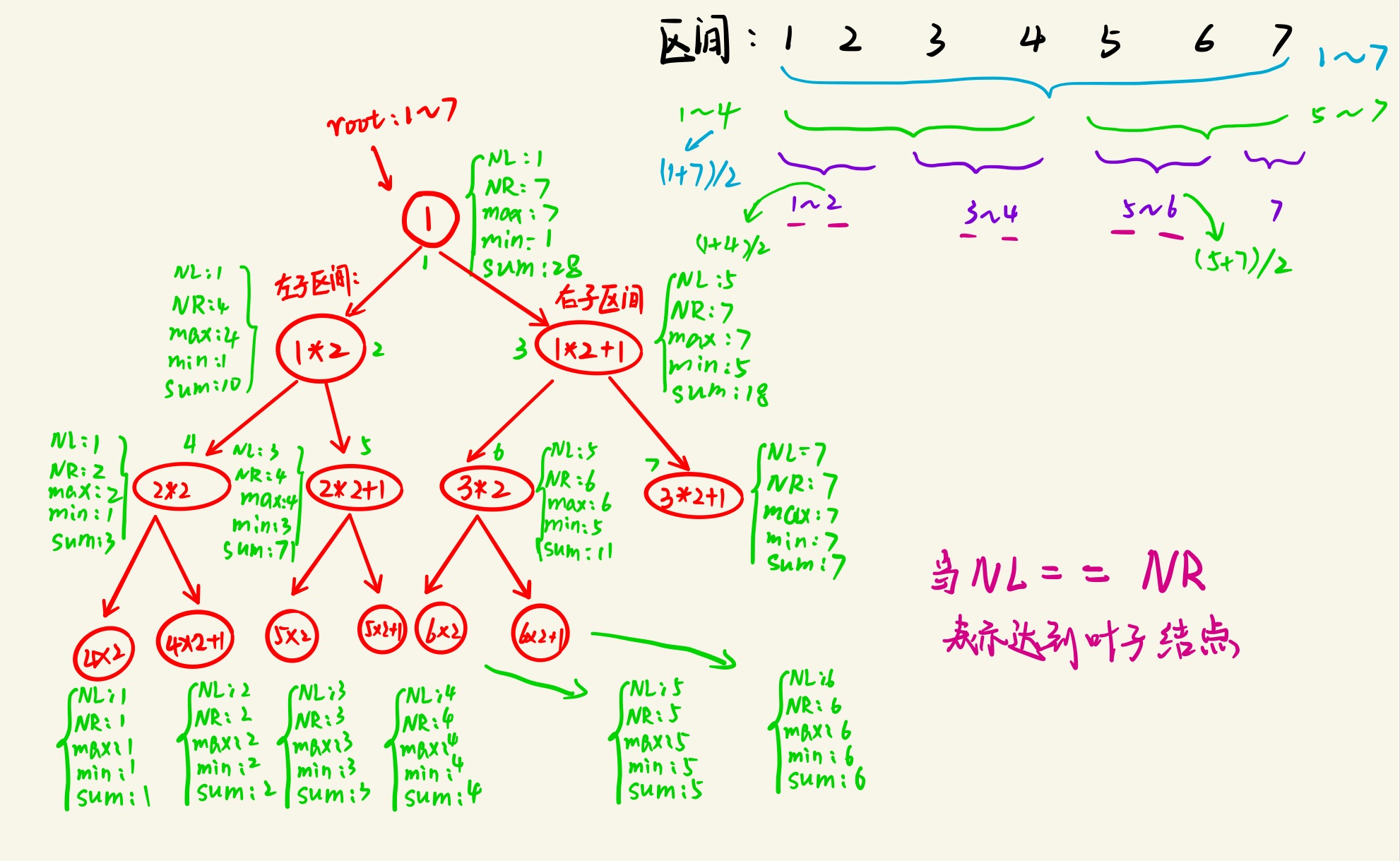
三.线段树的实例使用及代码
(1)实例背景

(2)建树
1>将7个红包建立为一颗线段树

2>建树代码
struct Tree {//定义结构 ll l,r;//节点左右端点 ll sum;//求和 ll lazy;//延迟标记 ll maxn;//最大值 ll minn;// 最小值 } t[MAXN<<2];//开4倍空间 void push_up(ll rt) { //向上更新 t[rt].sum = t[rt << 1].sum + t[rt << 1 | 1].sum;//更新和 t[rt].maxn = max(t[rt << 1].maxn ,t[rt << 1 | 1].maxn);//更新最大值 t[rt].minn = min(t[rt << 1].minn ,t[rt << 1 | 1].minn);//更新最小值 } void build(ll l,ll r, ll rt) { //建树,rt==root t[rt].lazy = 0; t[rt].l=l; t[rt].r=r; if(l == r) { scanf("%lld",&t[rt].sum);//单个红包时输入金额 t[rt].minn=t[rt].sum; t[rt].maxn=t[rt].sum; return; } ll mid = (l + r) >> 1; build(l,mid,rt<<1); build(mid+1,r,rt<<1|1); push_up(rt);//向上更新
}
(3)得到n~m的红包的金钱总额
1 #define ll long long 2 #define lson rt << 1 3 #define rson rt << 1 | 1 4 5 void push_down(ll rt, ll m) {//pushdown函数 6 if(t[rt].lazy) { //若有标记,则将标记向下移动一层 7 t[rt << 1].lazy += t[rt].lazy; 8 t[rt << 1 | 1].lazy += t[rt].lazy; 9 t[rt << 1].sum += (m - (m >> 1)) * t[rt].lazy; 10 t[rt << 1 | 1].sum += (m >> 1) * t[rt].lazy; 11 t[rt << 1].minn += t[rt].lazy; 12 t[rt << 1 | 1].minn+= t[rt].lazy; 13 t[rt << 1].maxn += t[rt].lazy; 14 t[rt << 1 | 1].maxn+= t[rt].lazy; 15 t[rt].lazy = 0;//取消本层标记 16 } 17 } 18 19 ll query(ll L, ll R, ll rt) { //区间求和 20 if(L <= t[rt].l && R >= t[rt].r) {//如果当前节点所代表的区间包含于所求区间 21 return t[rt].sum;//直接返回sum 22 } 23 push_down(rt, t[rt].r - t[rt].l + 1);//向下更新,对lazy标记进行处理 24 ll mid = (t[rt].r + t[rt].l) >> 1; 25 ll ans = 0; 26 if(L <= mid) ans += query(L, R, lson);//分两边递归 27 if(R > mid) ans += query(L, R, rson); 28 return ans; 29 }
(4)更新n~m的金钱数
void update(ll L,ll R, ll key, ll rt) { //区间更新 if(L <= t[rt].l && R >= t[rt].r) { t[rt].sum+=(t[rt].r - t[rt].l + 1) * key; t[rt].minn+=key; t[rt].maxn+=key; t[rt].lazy+=key; return; } push_down(rt, t[rt].r - t[rt].l + 1);//向下更新 ll mid = (t[rt].r + t[rt].l) >> 1; if(L <= mid) update(L, R, key, lson); if(R > mid) update(L, R, key, rson); push_up(rt);//向上更新 }
(5)寻找最值
ll query_min(ll L, ll R, ll rt) { //区间求最小值
if(L <= t[rt].l && R >= t[rt].r) {
return t[rt].minn;
}
push_down(rt, t[rt].r - t[rt].l + 1);//向下更新
ll mid = (t[rt].r + t[rt].l) >> 1;
ll ans = 0x3f3f3f3f;
if(L <= mid) ans = min(ans,query_min(L, R, lson));
if(R > mid) ans =min(ans,query_min(L, R, rson)) ;
return ans;
}
ll query_max(ll L, ll R, ll rt) { //区间求最大值
if(L <= t[rt].l && R >= t[rt].r) {
return t[rt].maxn;
}
push_down(rt, t[rt].r - t[rt].l + 1);//向下更新
ll mid = (t[rt].r + t[rt].l) >> 1;
ll ans = 0;
if(L <= mid) ans = max(ans,query_max(L, R, lson));
if(R > mid) ans = max(ans,query_max(L, R, rson));
return ans;
}