objectarx之（点集）凸包算法

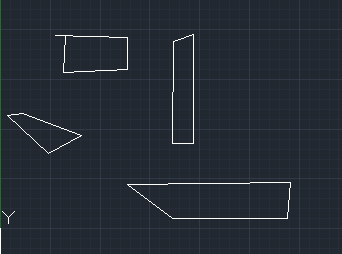
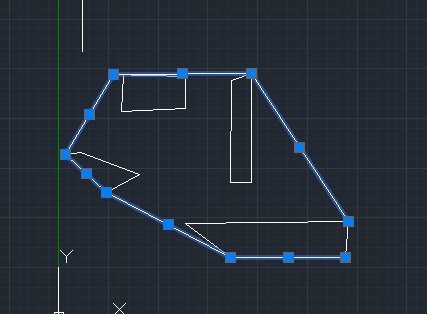
ConvexHull.h文件：

#pragma once
#include <algorithm>
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;
//二维点(或向量)结构体定义

typedef struct PointStruct
{
double x;
double y;
}POINT1;

class CConvexHull
{
public:
CConvexHull();
~CConvexHull();

public:
typedef vector<POINT1> PTARRAY;
static bool CompareVector(const POINT1 &pt1, const POINT1 &pt2);
static void CalcConvexHull(PTARRAY &vecSrc);
};

CConvexHull.cpp文件：

#include "stdafx.h"
#include "ConvexHull.h"

CConvexHull::CConvexHull()
{
}

CConvexHull::~CConvexHull()
{
}

//判断两个点(或向量)是否相等
bool operator==(const POINT1 &pt1, const POINT1 &pt2)
{
return (pt1.x == pt2.x && pt1.y == pt2.y);
}

// 比较两个向量pt1和pt2分别与x轴向量(1, 0)的夹角
bool CConvexHull::CompareVector(const POINT1 &pt1, const POINT1 &pt2)
{

//求向量的模
float m1 = sqrt((float)(pt1.x * pt1.x + pt1.y * pt1.y));
float m2 = sqrt((float)(pt2.x * pt2.x + pt2.y * pt2.y));
//两个向量分别与(1, 0)求内积
float v1 = pt1.x / m1, v2 = pt2.x / m2;
return (v1 > v2 || (v1 == v2 && m1 < m2));

}

//计算凸包
void CConvexHull::CalcConvexHull(PTARRAY &vecSrc)
{
//点集中至少应有3个点，才能构成多边形
if (vecSrc.size() < 3) {
return;
}
//查找基点
POINT1 ptBase = vecSrc.front(); //将第1个点预设为最小点
for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
//如果当前点的y值小于最小点，或y值相等，x值较小
if (i->y < ptBase.y || (i->y == ptBase.y && i->x > ptBase.x)) {
//将当前点作为最小点
ptBase = *i;
}
}
//计算出各点与基点构成的向量
for (PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end();) {
//排除与基点相同的点，避免后面的排序计算中出现除0错误
if (*i == ptBase) {
i = vecSrc.erase(i);
}
else {
//方向由基点到目标点
i->x -= ptBase.x, i->y -= ptBase.y;
++i;
}
}
//按各向量与横坐标之间的夹角排序
sort(vecSrc.begin(), vecSrc.end(), &CompareVector);
//删除相同的向量
vecSrc.erase(unique(vecSrc.begin(), vecSrc.end()), vecSrc.end());
//计算得到首尾依次相联的向量
for (PTARRAY::reverse_iterator ri = vecSrc.rbegin();
ri != vecSrc.rend() - 1; ++ri) {
PTARRAY::reverse_iterator riNext = ri + 1;
//向量三角形计算公式
ri->x -= riNext->x, ri->y -= riNext->y;
}
//依次删除不在凸包上的向量
for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
//回溯删除旋转方向相反的向量，使用外积判断旋转方向
for (PTARRAY::iterator iLast = i - 1; iLast != vecSrc.begin();) {
int v1 = i->x * iLast->y, v2 = i->y * iLast->x;
//如果叉积小于0，则无没有逆向旋转
//如果叉积等于0，还需判断方向是否相逆
if (v1 < v2 || (v1 == v2 && i->x * iLast->x > 0 &&
i->y * iLast->y > 0)) {
break;
}
//删除前一个向量后，需更新当前向量，与前面的向量首尾相连
//向量三角形计算公式
i->x += iLast->x, i->y += iLast->y;
iLast = (i = vecSrc.erase(iLast)) - 1;
}
}
//将所有首尾相连的向量依次累加，换算成坐标
vecSrc.front().x += ptBase.x, vecSrc.front().y += ptBase.y;
for (PTARRAY::iterator i = vecSrc.begin() + 1; i != vecSrc.end(); ++i) {
i->x += (i - 1)->x, i->y += (i - 1)->y;
}
//添加基点，全部的凸包计算完成
vecSrc.push_back(ptBase);
}

 test：

CConvexHull::PTARRAY vecSrc, vecCH;
for (int i = 0; i < pts.length(); ++i)
{
POINT1 ptIn = { pts[i].x, pts[i].y };
vecSrc.push_back(ptIn);
//cout << ptIn.x << ", " << ptIn.y << endl;
}
CConvexHull::CalcConvexHull(vecSrc);
//cout << " Convex Hull: ";
for (CConvexHull::PTARRAY::iterator i = vecSrc.begin(); i != vecSrc.end(); ++i) {
//cout << i->x << ", " << i->y << endl;
acutPrintf(_T(" %2f,%2f,0"), i->x, i->y);

}

}

效果：