A
- PZ's solution:
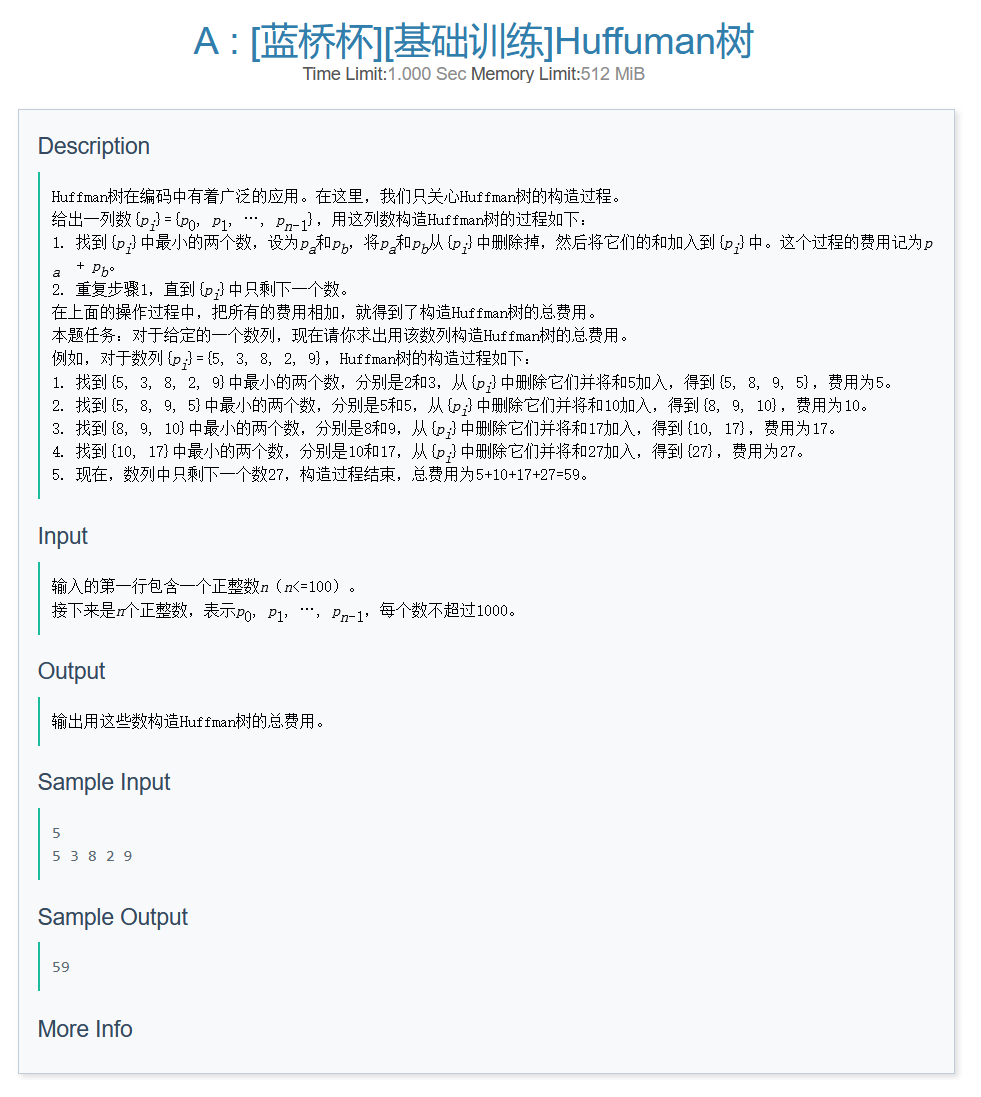
1.根据题意模拟即可,不过难点在于每次寻找({p_i})中的两个最小值;
2.使用(overset{priority\_queue}{优先队列})维护即可,不过优先队列默认维护大根堆,可以采取入队负数的方法维护小根堆;
- TAG:贪心;优先队列
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
priority_queue<int>q;
int n,x,y,ans;
int main(){
scanf("%d",&n);
while(n--){
int x; scanf("%d",&x);
q.push(-x);
}
while(q.size()>1){
x=-q.top(); q.pop();
y=-q.top(); q.pop();
ans+=x+y;
q.push(-(x+y));
}
printf("%d",ans);
return 0;
}
B

- Solution:
- 思路借鉴于ciyou的题解 P1016 【旅行家的预算】
1.本题有几个思考点:
①到达某个加油站时,是否需要加油?这取决于此加油站的油价;
②到达某个加油站时,需要加多少油?考虑贪心,需要对比前后加油站的油价,并且考虑加油后能否到达油价更低的地方,或者考虑能从油价更低的地方过来而不在此处买油;
2.考虑使用优先队列来处理思考点:
①到达某个加油站时,最多能加容量为(C)的油,此地油价为(P_i);
②而在达到此加油站之前,需要驾驶的距离,设为(dis_{now});
③用优先队列维护之前到达加油站的油价(cost)和剩余可以加的油量(rest);
④从队列中取出油价最小的油量,来尝试走完这段距离,然后不断重复这个过程;
⑤如果此时队列空了,说明不论如何加油都达到不了下一个加油站,说明此用例无解;
⑥如果能够走完,代表可以到达此加油站,并且保证了使用的油的价格是最便宜的,因为题目要求的答案是花费最少,这就自然符合了我们的预期;
3.这里再做详细的思考,如何保证优先队列中取出来的油是合法的?如果走的路程过长,再取油不就“过期”了吗?
但其实并不会这样,因为优先队列维护的是剩余可以加的油量(rest),所以只要能用,就一定可以在中间某一段,加上优先队列中维护的油;
而且不必担心 因为要加便宜油,反而使前面的路出现了还没有到便宜油站就加上便宜油 的情况,因为在2.中的过程保证了在到达此加油站时的油的花费都是合法的,所以就没有这种问题了。
- TAG:贪心;优先队列
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef struct Node{
double cost,rest;
bool operator <(const Node &x) const{
return cost>x.cost;
}
Node(double _cost,double _rest) :cost(_cost),rest(_rest){};
}Node;
priority_queue<Node>q;
double D1,C,D2,P1,D[10],P[10],ans,dis[10],now_dis;
int N;
int main(){
scanf("%lf %lf %lf %lf %d",&D1,&C,&D2,&P1,&N);
for(int i=1;i<=N;++i) scanf("%lf %lf",&D[i],&P[i]);
//将终点和各个加油站之间的距离进行预处理
D[++N]=D1; for(int i=N;i>=1;--i) D[i]-=D[i-1];
q.push(Node(P1,C));
for(int i=1;i<=N;++i){
now_dis=D[i];
while(now_dis){
if(q.empty()){ puts("No Solution"); return 0; }
//优先队列为空,说明了无油可买,到达不了目的地
Node tmp=q.top(); q.pop();
//如果现在队列头部的油量就可以走完全程
if(tmp.rest*D2>=now_dis){
tmp.rest-=now_dis/D2;
ans+=tmp.cost*now_dis/D2;
q.push(Node(tmp.cost,tmp.rest));
break;
} else {
//如果走不完,只能走一部分
now_dis-=tmp.rest*D2;
ans+=tmp.rest*tmp.cost;
}
}
//能走到此加油站,那么将其油价和油量入队
q.push(Node(P[i],C));
}
printf("%.2lf",ans);
return 0;
}
C

- Solution:
思路借鉴于ice--cream的完美的代价和C3Stones的蓝桥杯 基础练习 BASIC-19 完美的代价
1.首先,确定交换的方法:
①首先尝试第一个字符与最后一个字符配对:保持第一个字符本身不变,从后往前找到一个与其配对的字符,随后交换此字符与最后一个字符,完成配对;
②再次尝试第二个字符与倒数第二个字符配对,直到所有字符完成配对;
③思考,为何这种方法能保证交换次数最少:因为题目要求只能交换相邻的两个字符,所以这种寻找能保证找到最邻近的配对,保证交换次数最少,不会发生因为交换而导致之后的配对的交换次数增加(因为这种交换后,除了配对的字符,其他字符顺序不受影响,而且受影响的字符也不会因为交换而导致答案增加,因为如果交换之后的字符能有更优的交换方法,它早就被交换到相应的位置了)
2.再次,思考奇数的情况和无解的情况:
①奇数的情况需要注意需要找到一个出现奇数次的字符,将其放到中间;
②但找到这个字符后,不需急着交换到中间,因为如果此数在(frac{n}{2})之前,那么交换之后,一旦有需要交换的数也在(frac{n}{2})之前,那么就需要多交换一次与这个字符的次数,这样会增加答案值,是不被期望的;
③因此,只需找到此字符的位置,计算其与中间位置的交换次数即可,待其他字符配对完成,加上此次数即为答案,这也是唯一影响最优交换次数的交换,这不是配对交换中普遍存在的,这是由于其位置的特殊性造成的;
④考虑无解的情况:第一种即偶数长度的字符串出现了奇数次的字符,显然非法;第二种即奇数长度的字符串,出现了两种奇数次的字符,那么中间位置就存在两种字符选择,显然非法;
- TAG:字符串;回文
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,ans,p;
bool f;
char s[8005];
int main(){
scanf("%d",&n);
scanf("%s",s+1);
p=n;
for(int i=1;i<p;++i)
for(int j=p;j>=i;--j)
//需要先判断i==j,因为此位置必然存在s[i]==s[j],不存在配对交换一说
if(i==j){
//i==j时,表明找不到配对字符,说明其为出现了奇数次的字符
//f代表是否出现了奇数次的字符,看如下判断
//①如果是偶数次,并且i==j说明出现了奇数次字符,无解
//②如果已经出现过奇数次字符,还会回到此判断,说明出现了二个及以上奇数次字符,无解
if(n%2==0 || f){
puts("Impossible");
return 0;
}
f=1;
//奇数次情况,计算此字符到中间位置的交换次数
//但需要注意的是,此字符到中间位置并不必须经过这个语句,可能之前的交换语句就可以
//实现其交换到中间位置的结果,而这种交换并不会造成答案过多的影响,因为这种交换本身就是
//在不产生多余交换次数下进行的
ans+=n/2+1-i;
} else if(s[i]==s[j]){
for(int k=j;k<p;++k){
swap(s[k],s[k+1]);
++ans;
}
--p;
break;
}
printf("%d",ans);
return 0;
}
D
- Solution:
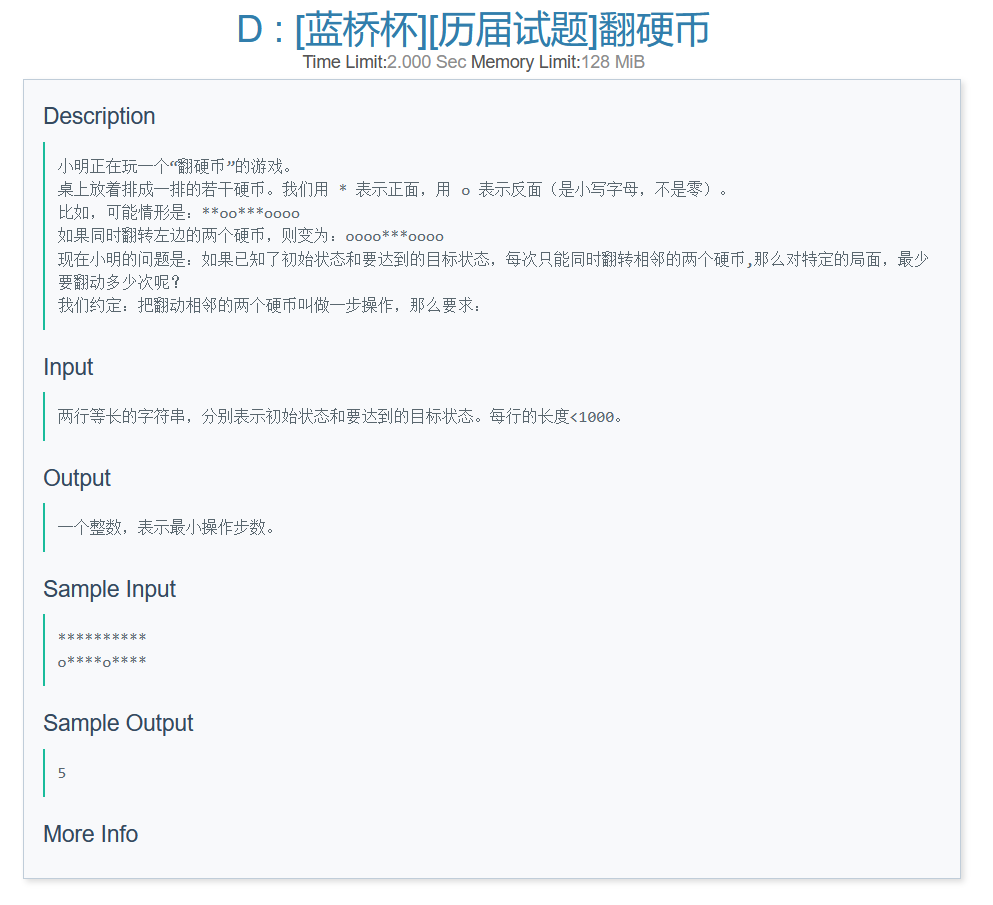
思路借鉴于(\_天道酬勤\_不忘初心)的蓝桥杯 历届试题 翻硬币(贪心)
1.将题目问题转换一下,将上下字符串进行比较,相同即为0,不同即为1,因为初始状态本身并不对答案作出贡献,只需要关心目标状态与初始状态的不同即可;
2.由于每次只能反转两个相邻的硬币,此题与C题其实也有千丝万缕的联系:
①对于10...01的情况,可以发现从左往右翻转硬币,即可使硬币全部翻转为0,答案即为两个1坐标的差值;
②如果出现01011010的情况,最受关注的,还是是否应该先将11翻转过去,但其实,这样反而会让答案增大,为什么呢?
因为一旦将11反转,其就会变为01000010,那么1和1之间的坐标差值会比之前变大;
不反转时,可以将其拆为0101和1010,但翻转11之后就会增加11位置的答案贡献,这显然不是最优的;
3.另外,题目其实隐藏了一个条件,即1一定是偶数个数,为什么呢?
①首先,题目一定有解法,那么翻转一次,就一定会产生2个位置与初始状态不同;
②即使再次翻转,情况也无非是两种,一种是在新的地方翻转两个新的硬币,这样会增加2个位置与初始状态不同;另一种就是在原来11的基础上变为101,可以发现这种情况一定会导致1个位置回到初始状态而增加1个不同位置;
③所以,无论如何翻转,1的个数一定是偶数;
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
string s1,s2;
int ans,p;
int main(){
getline(cin,s1);
getline(cin,s2);
p=-1;
for(int i=0;i<s1.size();++i)
if(s1[i]!=s2[i])
if(p==-1) p=i;
else{
ans+=i-p;
p=-1;
//在这里p重新置为-1,因为本体的原理其实是将01串拆分成数个
//10..01(可能中间没有0)的情况,这样是依此对两个1之间算位置差值
//这是以两个为一对的基础上进行的
}
printf("%d",ans);
return 0;
}
E

- PZ's solution:
对于每个雷,其周围所有的答案(+1)即可;
- TAG:模拟;签到题
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,m,ans[105][105];
char mp[105][105];
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j){
cin>>mp[i][j];
if(mp[i][j]=='*'){
ans[i-1][j]+=1;
ans[i+1][j]+=1;
ans[i][j-1]+=1;
ans[i][j+1]+=1;
ans[i-1][j-1]+=1;
ans[i-1][j+1]+=1;
ans[i+1][j-1]+=1;
ans[i+1][j+1]+=1;
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
if(mp[i][j]=='*') putchar('*');
else printf("%d",ans[i][j]);
puts("");
}
return 0;
}
F
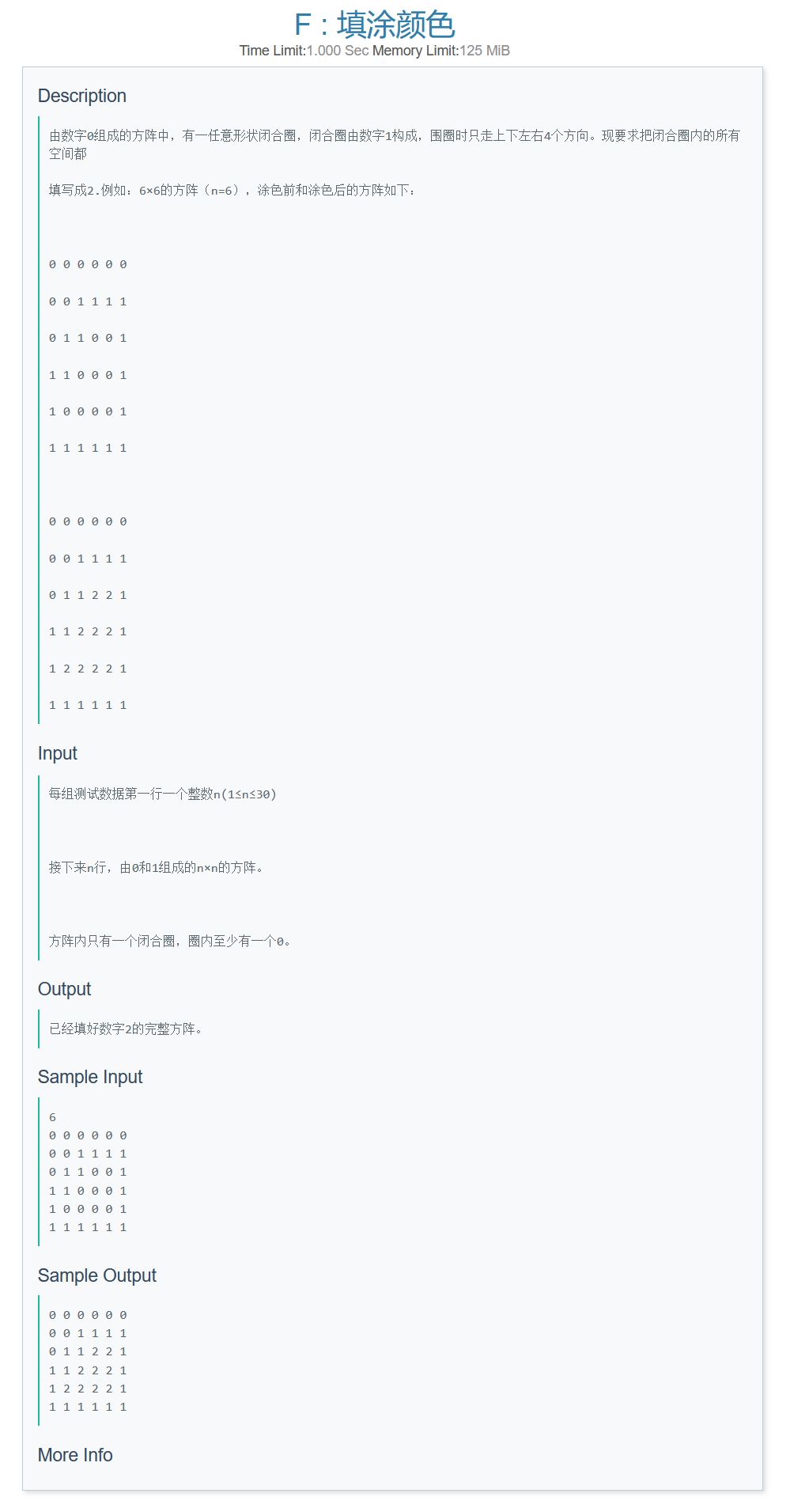
- PZ's solution:
对于被圈住的0的区域的左上角,一定存在其左边和上边均为1,找到这个点开始BFS即可;
- TAG:BFS广度优先搜索
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
queue<int>qx,qy;
int n,mp[35][35],sx,sy;
int fx[]={0,0,1,-1};
int fy[]={1,-1,0,0};
bool check(int x,int y){ return 1<=x&&x<=n&&1<=y&&y<=n; }
void bfs(){
qx.push(sx); qy.push(sy);
while(!qx.empty()){
int x=qx.front(),y=qy.front(); qx.pop(); qy.pop();
for(int i=0;i<4;++i){
int nx=x+fx[i],ny=y+fy[i];
if(!check(nx,ny)||mp[nx][ny]) continue;
mp[nx][ny]=2;
qx.push(nx); qy.push(ny);
}
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
scanf("%d",&mp[i][j]);
if(!sx&&mp[i][j]==0&&mp[i-1][j]==1&&mp[i][j-1]==0)
sx=i,sy=j;
}
bfs();
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
printf("%d%c",mp[i][j],(j==n ? '
' : ' '));
return 0;
}
G

- PZ's solution:
直接计算,看得数是否相同即可;
- TAG:模拟;签到题
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int main(){
long long a=1,b=1;
int l1,l2;
string s1,s2;
cin>>s1; l1=s1.size();
cin>>s2; l2=s2.size();
for(int i=0;i<l1;i++) a=a*((int)s1[i]-64);
for(int i=0;i<l2;i++) b=b*((int)s2[i]-64);
a=a%47; b=b%47;
if(a==b) cout<<"GO";
else cout<<"STAY";
return 0;
}
H

- Solution:
思路借鉴于DeadWooder的轻重搭配
1.显然,首先,最多搭配(frac{n}{2})组,考虑贪心:
①如果依照最瘦的人和最重的人组队,可能导致最中间的两个人因为体重相似而无法配对;
②那么让最瘦的和其能最小配对的人组队,就最优了吗?并不,因为如果最瘦的人过瘦,可能导致其和次瘦的人配对,导致次瘦的人无法与更胖的人配对;
③考虑最多搭配(frac{n}{2})组,那么对身高进行排序,让前(frac{n}{2})的人和后(frac{n}{2})的人进行配对;
④为什么这样贪心合理呢?不怕前(frac{n}{2})中有配对才最优的情况吗?事实上,这种情况是不存在的,因为题目表示体重为(x)的人能配对体重至少为(2*x)的人,那么如果说前(frac{n}{2})中有能配对的情况,那必然也会存在其中较小的一个人可以和后(frac{n}{2})中的一人配对,因为体重越重,其实配对越容易;
2.所以,对身高排序分为两组,配对即可;
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,a[500005],ans;
bool vis[500005];
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i) scanf("%d",&a[i]);
sort(a+1,a+1+n);
int p=1;
for(int i=n/2+1;i<=n;++i)
if(2*a[p]<=a[i]){
++ans;
vis[p]=vis[i]=1;
++p;
}
for(int i=1;i<=n;++i) if(!vis[i]) ++ans;
printf("%d",ans);
return 0;
}
赛后总结
1.本次题目不是递增的(っ °Д °;)っ,写题需谨慎啊!
2.A题本身就是优先队列(堆)的模板题目,而B题是对优先队列的进阶应用;
3.C题和D题都涉及了相邻元素交换的贪心,在贪心的正确性论证上,是有一定难度的;
4.E、F、G题其实本身与贪心无关,属于签到题目;
5.H题本身不难,但需要注意理解题意,即到底谁和谁能配对,重新理解题意可以对题目有更好的理解,对解题可能有重大的突破;