博客迁移计划14
E. Tourists
There are $ n $ cities in Cyberland, numbered from $ 1 $ to $ n $ , connected by m bidirectional roads.
The $ j $ -th road connects city $ a_j $ and $ b_j $ .
For tourists, souvenirs are sold in every city of Cyberland. In particular, city $ i $ sell it at a price of $ w_i $ .
Now there are $ q $ queries for you to handle. There are two types of queries:
-
" C $ a w $ ": The price in city $ a $ is changed to $ w $.
-
" A $ a b $ ": Now a tourist will travel from city $ a $ to $ b $ .
He will choose a route, he also doesn't want to visit a city twice.
He will buy souvenirs at the city where the souvenirs are the cheapest (possibly exactly at city $ a $ or $ b $ ).
You should output the minimum possible price that he can buy the souvenirs during his travel.
More formally, we can define routes as follow:
-
A route is a sequence of cities $ [x_1, x_2, ..., x_k] $ , where $ k $ is a certain positive integer.
-
For any $ 1 ≤ i < j ≤ k, xi ≠ xj $ .
-
For any $ 1 ≤ i < k $ , there is a road connecting $ x_i $ and $ x_{i + 1} $ .
-
The minimum price of the route is $ min(w_{x_1}, w_{x_2}, ..., w_{x_k}) $ .
-
The required answer is the minimum value of the minimum prices of all valid routes from $ a $ to $ b $ .
Input
The first line of input contains three integers $ n, m, q (1 ≤ n, m, q ≤ 10^5) $ , separated by a single space.
Next $ n $ lines contain integers $ w_i (1 ≤ w_i ≤ 10^9) $ .
Next $ m $ lines contain pairs of space-separated integers $ a_j $ and $ b_j (1 ≤ a_j, b_j ≤ n, a_j ≠ b_j) $ .
It is guaranteed that there is at most one road connecting the same pair of cities.
There is always at least one valid route between any two cities.
Next $ q $ lines each describe a query. The format is " C $ a w $ " or " A $ a b $ " $ (1 ≤ a, b ≤ n, 1 ≤ w ≤ 10^9) $ .
Output
For each query of type "A", output the corresponding answer.
Examples
input1
3 3 3
1
2
3
1 2
2 3
1 3
A 2 3
C 1 5
A 2 3
output1
1
2
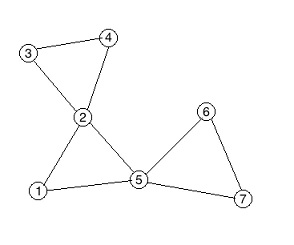
input2
7 9 4
1
2
3
4
5
6
7
1 2
2 5
1 5
2 3
3 4
2 4
5 6
6 7
5 7
A 2 3
A 6 4
A 6 7
A 3 3
output2
2
1
5
3
Note
For the second sample, an optimal routes are:
From $ 2 $ to $ 3 $ it is $ [2, 3] $ .
From $ 6 $ to $ 4 $ it is $ [6, 5, 1, 2, 4] $ .
From $ 6 $ to $ 7 $ it is $ [6, 5, 7] $ .
From $ 3 $ to $ 3 $ it is $ [3] $ .
题目大意
-
$ n $ 个点 $ m $ 条边的无向图,每个点的纪念品都有一个价格,执行 $ q $ 次操作,分为两类
-
改变一个点的纪念品价格
-
询问 $ x $ 到 $ y $ 的任意简单路径上最便宜的纪念品
-
$ n,m,q \le 100000$
题解
结论:一个点数大于等于3的点双连通分量中对于任意不同的三点 $ a,b,c $ ,
必定存在一条简单路径从 $ a $ 走到 $ b $ 经过 $ c $ 。
-
一个 $ v-DCC $ 中的点肯定能通过简单路径互相到达
-
把点双连通分量缩点,形成一棵树,树上包括“割点”和“缩点后的新点”
-对于每个缩成的点,用 $ set $ 维护对应 $ v-DCC $ 中除了“最高割点”之外的纪念品的最小价格
- 换言之,割点纪念品的价格只在树上“割点”本身和它父亲对应的 $ v-DCC $ 中维护
- 最后再加上动态树或树链剖分即可解决
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<stack>
#include<set>
using namespace std;
#define N 200005
multiset<int>s[N];
multiset<int>::iterator it;
vector<int>e[N],G[N];
stack<int>st;
int n,m,q,dfn[N],low[N],tim,cnt,w[N],bel[N];
bool vis[N];
void tarjan(int u,int fa){
dfn[u]=low[u]=++tim;
st.push(u); vis[u]=1;
for(int i=0;i<e[u].size();++i){
int v=e[u][i];
if(v==fa) continue;
if(!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
++cnt; int tmp;
G[u].push_back(cnt);
do{
tmp=st.top(); st.pop();
G[cnt].push_back(tmp);
s[cnt].insert(w[tmp]);
bel[tmp]=cnt;
}while(tmp!=v);
w[cnt]=*(s[cnt].begin());
}
} else if(vis[v])
low[u]=min(low[u],dfn[v]);
}
}
int siz[N],f[N],dep[N],son[N],top[N],id[N],wt[N];
void dfs1(int u){
siz[u]=1;
for(int i=0;i<G[u].size();++i){
int v=G[u][i];
dep[v]=dep[u]+1; f[v]=u;
dfs1(v);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf){
top[u]=topf;
wt[id[u]=++tim]=u;
if(son[u]) dfs2(son[u],topf);
for(int i=0;i<G[u].size();++i){
int v=G[u][i];
if(v==son[u]) continue;
dfs2(v,v);
}
}
int sum[N<<2];
void build(int o,int l,int r){
if(l==r){
sum[o]=w[wt[l]];
return;
}
int mid=l+r>>1;
build(o<<1,l,mid); build(o<<1|1,mid+1,r);
sum[o]=min(sum[o<<1],sum[o<<1|1]);
}
void updata(int o,int l,int r,int u,int val){
if(l==r){
sum[o]=val;
return;
}
int mid=l+r>>1;
if(u<=mid) updata(o<<1,l,mid,u,val);
else updata(o<<1|1,mid+1,r,u,val);
sum[o]=min(sum[o<<1],sum[o<<1|1]);
}
int check(int o,int l,int r,int u,int v){
if(u<=l&&r<=v){
return sum[o];
}
int res=1e9+7,mid=l+r>>1;
if(u<=mid) res=min(res,check(o<<1,l,mid,u,v));
if(v>mid) res=min(res,check(o<<1|1,mid+1,r,u,v));
return res;
}
void modify(int u,int val){
if(bel[u]){
it=s[bel[u]].find(w[u]);
s[bel[u]].erase(it);
}
w[u]=val;
updata(1,1,cnt,id[u],val);
if(bel[u]){
s[bel[u]].insert(w[u]);
w[bel[u]]=*(s[bel[u]].begin());
updata(1,1,cnt,id[bel[u]],w[bel[u]]);
}
}
int query(int u,int v){
int res=1e9+7;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]]) swap(u,v);
res=min(res,check(1,1,cnt,id[top[u]],id[u]));
u=f[top[u]];
}
if(dep[u]>dep[v]) swap(u,v);
res=min(res,check(1,1,cnt,id[u],id[v]));
if(u>n&&f[u]) res=min(res,w[f[u]]);
return res;
}
int main(){
scanf("%d %d %d",&n,&m,&q);
cnt=n;
for(int i=1;i<=n;++i) scanf("%d",&w[i]);
for(int i=1;i<=m;++i){
int u,v;
scanf("%d %d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
tarjan(1,0);
dfs1(1);
tim=0;
dfs2(1,0);
build(1,1,cnt);
while(q--){
char opt[1]; int x,y;
scanf("%s %d %d",opt,&x,&y);
if(opt[0]=='C') modify(x,y);
else printf("%d\n",query(x,y));
}
return 0;
}
/*
# 42550351
When 2018-09-06 14:42:23
Who PotremZ
Problem E - Tourists
Lang GNU C++11
Verdict Accepted
Time 421 ms
Memory 41800 KB
*/