P1219 [USACO1.5]八皇后 Checker Challenge

-
PZ's solution:
1.从每行开始搜索合法位置;
2.寻找一个合法位置,符合 列、主对角线、次对角线 均未被标记;
3.将此合法位置记录,将 列、主对角线、次对角线 标记;
4.寻找下一个合法位置,直到\(n\)行为止 ,搜索完毕;
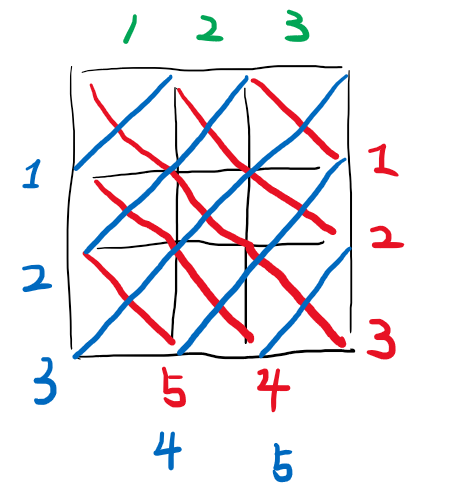
绿色为列标号,记 \(lie[i]\)为列标记;
红色为主对角线标号,记 \(zhu[i]\)为主对角线标记;
蓝色为次对角线标号,记\(ci[i]\)为次对角线标记;
观察\((1,1)\)位置,它在\(3\)号主对角线上。
向右移动到\((1,2)\)位置,它就变为在\(2\)号主对角线上,可以确认 列标号与主对角线负相关;
向下移动到\((2,1)\)位置,它就变为在\(4\)号主对角线上,可以确认 行标号与主对角线正相关;
主对角线共\(2*n-1\)条,可以猜想到位置与主对角线标号互换关系为\((x,y) \to n-i+x\)
同理,观察\((1,1)\)位置,它在\(1\)号次对角线上,
向右移动到\((1,2)\)位置,它就变为在\(2\)号次对角线上,可以确认 列标号与次对角线正相关;
向下移动到\((2,1)\)位置,它就变为在\(2\)号次对角线上,可以确认 行标号与次对角线正相关;
次对角线共\(2*n-1\)条,可以猜想到 位置与次对角线标号互换关系为\((x,y) \to i+x-1\)
- TAG:搜索;DFS深度优先搜索
P1219.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,tot,ans[14],lie[14],zhu[25],ci[25];
void dfs(int x){
if(x>n){
++tot;
if(tot<=3){
for(int i=1;i<=n;++i) printf("%d ",ans[i]);
putchar('\n');
}
return;
} else {
for(int i=1;i<=n;++i)
if(lie[i]==0 && ci[i+x-1]==0 && zhu[n-1-i+x]==0){
ans[x]=i;
lie[i]=ci[i+x-1]=zhu[n-1-i+x]=1;
dfs(x+1);
lie[i]=ci[i+x-1]=zhu[n-1-i+x]=0;
}
}
}
int main(){
scanf("%d",&n);
dfs(1);
printf("%d",tot);
return 0;
}
P2392 kkksc03考前临时抱佛脚

-
PZ's DFS solution:
1.考虑\(DFS\) ,用两个变量作为左右脑进行搜索;
2.每次都有两种选择,将当前题目交给左脑做,或者交给右脑做;
3.直到做完 全部题目 ,比较左右脑谁的时间更多,时间多的则 与答案进行比较;
4.由于递归的性质,所有情况都能被考虑到,\(DFS\)结束后即为最优答案;
-
PZ's DP solution:
1.观察性质,最优状态一定是 左右脑的用时相等;
2.考虑01背包,因为每道题只能做一次,设\(sum=\sum_{j=1}^{s_i}A_j\),将背包的上限设为\(\frac{sum}{2}\),
考虑到 题目所消耗的时间,故可视为 物品的大小和价值 均为题目的时间,可得到状态转移方程:
\[f[i]=max(f[i],f[i-A[j]+A[j]) \]3.因为可能有\(f[\frac{sum}{2}]\)凑不满的情况,显然有 \(sum-f[\frac{sum}{2}] \ge f[\frac{sum}{2}]\),故在累加答案时有\(ans=sum-f[\frac{sum}{2}]\)
-
TAG:搜索;DFS深度优先搜索;DP动态规划;背包;01背包
P2392 DFS.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
//使用 INT_MAX 需要 使用#include<climits>头文件
using namespace std;
int s[5],a[5][21],totr,totl,res,ans;
bool vis[5][21];
void dfs(int k,int x){
if(x>s[k]){
res=min(res,max(totl,totr));
return;
} else {
totl+=a[k][x];
dfs(k,x+1);
totl-=a[k][x];
totr+=a[k][x];
dfs(k,x+1);
totr-=a[k][x];
}
}
int main(){
for(int i=1;i<=4;++i) scanf("%d",&s[i]);
for(int i=1;i<=4;++i){
res=INT_MAX; totl=totr=0;
for(int j=1;j<=s[i];++j) scanf("%d",&a[i][j]);
dfs(i,1);
ans+=res;
}
printf("%d",ans);
return 0;
}
P2392 DP.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int s[5],a[65],f[1205],ans,sum;
int main(){
for(int i=1;i<=4;++i) scanf("%d",&s[i]);
for(int i=1;i<=4;++i){
sum=0;
memset(f,0,sizeof(f));
for(int j=1;j<=s[i];++j){ scanf("%d",&a[j]); sum+=a[j]; }
for(int j=1;j<=s[i];++j)
for(int k=sum/2;k>=a[j];--k)
f[k]=max(f[k],f[k-a[j]]+a[j]);
ans+=sum-f[sum/2];
}
printf("%d",ans);
return 0;
}
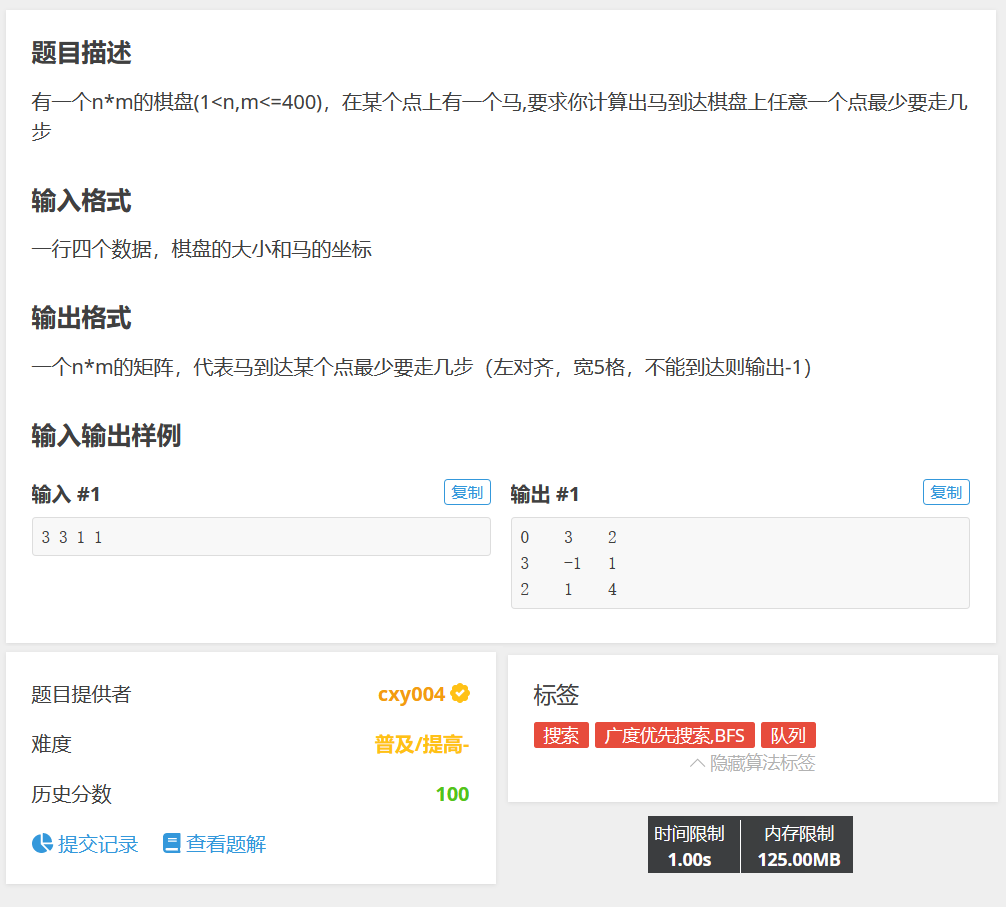
P1443 马的遍历
-
TAG:搜索;BFS广度优先搜索
广搜的模板题,注意马走日即可;
值得注意的一点:若视边权为\(1\),广搜时 每遍历到一个点,到达它的步数 即为 到达此处的最短路权。
P1443.cpp
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
int fx[]={2,2,-2,-2,1,1,-1,-1};
int fy[]={1,-1,1,-1,2,-2,2,-2};
int s[4000][4000],n,m,x,y;
void bfs(int x,int y){
memset(s,-1,sizeof(s));
queue<int>qx; queue<int>qy;
qx.push(x); qy.push(y); s[x][y]=0;
while(!qx.empty()){
x=qx.front(); y=qy.front(); qx.pop(); qy.pop();
for(int nx,ny,i=0;i<8;++i){
nx=x+fx[i]; ny=y+fy[i];
if(nx>0&&nx<=n&&ny>0&&ny<=m&&s[nx][ny]==-1){
s[nx][ny]=s[x][y]+1;
qx.push(nx); qy.push(ny);
}
}
}
}
int main(){
scanf("%d %d %d %d",&n,&m,&x,&y);
bfs(x,y);
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
printf("%-5d",s[i][j]);
puts("");
}
return 0;
}