$ ightarrow $ 戳我進BZOJ原題 $ ightarrow $ 戳我進洛谷原題
树网的核
时空限制 1000ms / 64MB
题目描述
设 $ T=(V,E,W) $ 是一个无圈且连通的无向图(也称为无根树),每条边到有正整数的权,
我们称 $ T $ 为树网(treebetwork),其中 $ V, E $ 分别表示结点与边的集合,$ W $ 表示各边长度的集合,并设 $ T $ 有 $ n $ 个结点。
路径:树网中任何两结点 $ a, b $ 都存在唯一的一条简单路径,用 $ d(a,b) $ 表示以 $ a, b $ 为端点的路径的长度,
它是该路径上各边长度之和。我们称 $ d(a, b) $ 为 $ a, b $ 两结点间的距离。
$ D(v,P)=min $ { $ d(v,u) $ } , $ u $ 为路径 $ P $ 上的结点。
树网的直径:树网中最长的路径成为树网的直径。对于给定的树网 $ T $,直径不一定是唯一的,
但可以证明:各直径的中点(不一定恰好是某个结点,可能在某条边的内部)是唯一的,我们称该点为树网的中心。
偏心距 $ ECC(F) $ :树网T中距路径F最远的结点到路径 $ F $ 的距离,即
$ ECC(F)=max $ { $ d(v,F),v∈V $ }
任务:对于给定的树网 $ T=(V,E,W) $ 和非负整数 $ s $ ,求一个路径 $ F $ ,
他是某直径上的一段路径(该路径两端均为树网中的结点),其长度不超过 $ s $ (可以等于 $ s $ ),使偏心距 $ ECC(F) $ 最小。
我们称这个路径为树网 $ T=(V,E,W) $ 的核(Core)。
必要时,$ F $ 可以退化为某个结点。
一般来说,在上述定义下,核不一定只有一个,但最小偏心距是唯一的。
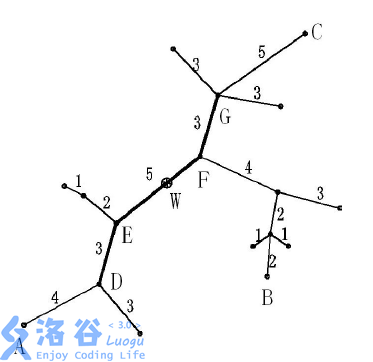
下面的图给出了树网的一个实例。
图中,$ A−B $ 与 $ A−C $ 是两条直径,长度均为 $ 20 $ 。
点 $ W $ 是树网的中心,$ EF $ 边的长度为 $ 5 $ 。
如果指定 $ s=11 $ ,则树网的核为路径 $ DEFG $(也可以取为路径 $ DEF $ ),偏心距为 $ 8 $ 。
如果指定 $ s=0 $ (或 $ s=1、s=2 $ ),则树网的核为结点 $ F $ ,偏心距为 $ 12 $ 。
输入输出格式
输入格式
共 $ n $ 行。
第 $ 1 $ 行,两个正整数 $ n $ 和 $ s $ ,中间用一个空格隔开。
其中 $ n $ 为树网结点的个数,$ s $ 为树网的核的长度的上界。设结点编号以此为 $ 1,2,…,n $ 。
从第 $ 2 $ 行到第 $ n $ 行,每行给出 $ 3 $ 个用空格隔开的正整数,依次表示每一条边的两个端点编号和长度。
例如,“ $ 2 quad 4 quad 7 $ ”表示连接结点 $ 2 $ 与 $ 4 $ 的边的长度为 $ 7 $ 。
输出格式
一个非负整数,为指定意义下的最小偏心距。
输入输出样例
输入样例#1
5 2
1 2 5
2 3 2
2 4 4
2 5 3
输出样例#1
5
输入样例#2
8 6
1 3 2
2 3 2
3 4 6
4 5 3
4 6 4
4 7 2
7 8 3
输出样例#2
5
说明
$ 40 $ %的数据满足:$ 5≤n≤15 $
$ 70 $ %的数据满足:$ 5≤n≤80 $
$ 100 $ %的数据满足:$ 5≤n≤300,0≤s≤1000 $ 。边长度为不超过 $ 1000 $ 的正整数
NOIP 2007 提高第四题
HINT
(BZOJ的数据)
对于 $ 70 $ %的数据,$ n le 200000 $
对于 $ 100 $ %的数据:$ n le 500000, s<2^{31} $ , 所有权值 $ <500 $
題解
-
樹的直徑不唯一,但所有直徑必定相交,并且各直徑的中點匯聚于同一處。
-
進一步可以得到一個推論:在任意一條直徑上求出的最小偏心距都相等。
-
於是,我們首先任意找到一條直徑。
- 解法一:枚舉 $ O(n^3) $
在直徑上枚舉距離不超過 $ s $ 的兩個點 $ p $ 和 $ q $ 作爲“核”, $ DFS $ 求偏心距
- 解法二:枚舉+貪心 $ O(n^2) $
根據貪心策略,在 $ p $ 固定后,另一端 $ q $ 在距離不超過 $ s $ 的前提下,顯然越遠越好。
所以只需要枚舉 $ p $ ,不用枚舉 $ q $
-
解法三:二分答案 $ O(n log SUM) $
-
本題的答案具有單調性,可以二分答案,把問題轉化爲:
-
“驗證是否存在一個核,其偏心距不超過二分的值 $ mid $ ” 。
-
在直徑上找到:距離不超過 $ mid $ 的前提下,離兩端最遠的節點,分別作爲節點 $ p, q $ 。
-
根據直徑的最長性,只需檢查 $ p, q $ 之間的路徑能否構成滿足條件的”核“
-
解法四:分析性質,直接掃描 $ O(n) $
-
設直徑上的節點為 $ u_1,u_2, dots ,u_t $
-
$ DFS $ 求出 $ d[u_i] $ ,表示從 $ u_i $ 出發,不經過直徑上的其他節點,能夠到達的最遠點的距離
-
以 $ u_i, u_j ( i le j ) $ 為端點的樹網的核的偏心距就是
-
$ max(max_{i le k le j}d[u_k], quad dist(u_1,u_i), quad dist(u_j,u_t) = max(max_{1 le k le t}d[u_k], quad ,dist(u_1,u_i), quad dist(u_j,u_t)) $
-
$ max_{1 le k le t }d[u_k] $ 對於 $ u_i , u_j $ 來説是一個定值
-
只需要枚舉直徑上的每個點 $ u_i $ ,用一個指針單調向後移動,即可得到 $ u_j $ 並更新答案
代碼
/**************************************************************
Problem: 1999
User: PotremZ
Language: C++
Result: Accepted
Time:2580 ms
Memory:39768 kb
****************************************************************/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define maxn 500010
struct edge{ int v,w; };
vector<edge>e[maxn];
int n,s,dis[maxn],f[maxn],d,ans=1e9+7;
bool vis[maxn];
void add(int u,int v,int w){ e[u].push_back((edge){v,w}); }
void dfs(int u,int fa){
f[u]=fa;
for(int i=0;i<e[u].size();++i)
if(!vis[e[u][i].v]&&e[u][i].v!=fa){
dis[e[u][i].v]=dis[u]+e[u][i].w;
dfs(e[u][i].v,u);
}
}
int main(){
scanf("%d %d",&n,&s);
for(int u,v,w,i=1;i<n;++i){
scanf("%d %d %d",&u,&v,&w);
add(u,v,w); add(v,u,w);
}
dfs(1,0); for(int i=1;i<=n;++i) if(dis[i]>dis[d]) d=i;
dis[d]=0; dfs(d,0); for(int i=1;i<=n;++i) if(dis[i]>dis[d]) d=i;
int j=d;
for(int i=d;i;i=f[i]){
while(f[j]&&dis[i]-dis[f[j]]<=s) j=f[j];
ans=min(ans,max(dis[j],dis[d]-dis[i]));
}
for(int i=d;i;i=f[i]){ vis[i]=1; dis[i]=0; dfs(i,f[i]); }
for(int i=1;i<=n;++i) ans=max(ans,dis[i]);
printf("%d",ans);
return 0;
}