Contest Hunter CH6201 走廊泼水节 最小生成树 Kruskal

$ ightarrow $ 戳我进CH原题

走廊泼水节 0x60「图论」例题

**总时限10 s $ quad $ 总内存256 MiB **
　

描述

【简化版题意】给定一棵N个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。
求增加的边的权值总和最小是多少。
　
我们一共有 $ N $ 个OIER打算参加这个泼水节，同时很凑巧的是正好有 $ N $ 个水龙头(至于为什么，我不解释)。
$ N $ 个水龙头之间正好有 $ N-1 $ 条小道，并且每个水龙头都可以经过小道到达其他水龙头(这是一棵树，你应该懂的..)。
但是OIER门为了迎接中中的挑战，决定修建一些个道路(至于怎么修，秘密~),
使得每个水龙头到每个水龙头之间都有一条直接的道路连接(也就是构成一个完全图呗~)。
但是OIER门很懒得，并且记性也不好，他们只会去走那 $ N-1 $ 条小道，
并且希望所有水龙头之间修建的道路，都要大于两个水龙头之前连接的所有小道(小道当然要是最短的了)。
所以神COW们，帮那些OIER们计算一下吧，修建的那些道路总长度最短是多少，毕竟修建道路是要破费的~~
　

输入格式

本题为多组数据~
第一行 $ t $ ，表示有t组测试数据
对于每组数据
第一行 $ N $ ，表示水龙头的个数（当然也是OIER的个数）；
$ 2 $ 到 $ N $ 行，每行三个整数 $ X,Y,Z $ ；表示水龙头 $ X $ 和水龙头 $ Y $ 有一条长度为 $ Z $ 的小道
　

输出格式

对于每组数据，输出一个整数，表示修建的所有道路总长度的最短值。
　

样例输入

 2
 3
 1 2 2
 1 3 3
 4
 1 2 3
 2 3 4
 3 4 5 

样例输出

 4
 17

　

数据范围与约定

每个测试点最多 $ 10 $ 组测试数据
$ 50 $ % $ n le 1500 $ ;
$ 100 $ % $ n le 6000 $ ;
$ 100 $ % $ z le 100 $ ;
　

样例解释

第一组数据，在 $ 2 $ 和 $ 3 $ 之间修建一条长度为 $ 4 $ 的道路，
使这棵树变成一个完全图，且原来的树依然是这个图的唯一最小生成树.
　

题解

• 对给定树上的 $ N-1 $ 条边模拟一遍 $ Kruskal $

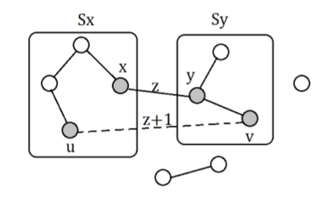
• 通过边 $ (x,y) $ 合并两个并查集

• $ x $ 集合中的每个点到 $ y $ 集合中的每个点

• 添加一条长度为 $ w(x,y)+1 $ 的边

代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 6010
struct edge{ int u,v,w; }e[maxn];
int t,n,f[6010],s[6010];
long long ans;
bool cmp(edge x,edge y){ return x.w<y.w; }
int find(int x){
	if(f[x]!=x) f[x]=find(f[x]);
	return f[x];
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=1;i<=n;++i){ f[i]=i; s[i]=1; }
		for(int i=1;i<n;++i) scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].w);
		sort(e+1,e+n,cmp); 
		ans=0;
		for(int fu,fv,i=1;i<n;++i){
			fu=find(e[i].u); fv=find(e[i].v);
			if(fu==fv) continue;
			ans+=1ll*(e[i].w+1)*(s[fu]*s[fv]-1);
			f[fu]=fv;
			s[fv]+=s[fu];
		}
		printf("%lld
",ans);
	}
	return 0;
}
/*
用时
32 ms
占用内存 
384 KiB
*/