【jzoj 5852】相交
Description
Input
Output
Sample Input
输入 1
8
1 2
1 3
2 4
2 5
5 6
5 7
3 8
4
2 5 4 3
5 3 8 8
5 4 6 7
4 8 6 7
输入 2
15
2 1
3 1
4 2
5 3
6 2
7 2
8 5
9 3
10 6
11 5
12 7
13 11
14 1
15 1
5
1 2 3 4
4 7 1 9
2 3 7 9
2 6 7 8
2 1 6 8
Sample Output
输出 1
YES
NO
YES
NO
输出 2
YES
NO
YES
YES
YES
Data Constraint
题解
-
求树上两条路径是否有点重合。
-
首先求出两条路径分别的$ LCA_1, LCA_2 $
如果其深度相同但是两个 $ LCA $ 却不相同,输出 NO
如果深度不同,用深度较深的 $ LCA $ 和另一条的路径的两点分别再求两次 $ LCA $
如果其中一次的 $ LCA = $ 深度较深的原 $ LCA $ ,就输出 YES ,否则输出 NO
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
inline void read(int &x){
char ch;x=0;
while(ch=getchar(),ch<'0'||ch>'9');x=ch-48;
while(ch=getchar(),ch>='0'&&ch<='9')x=10*x+ch-48;
}
int to[200005],nxt[200005],head[100005],tot;
inline void add(int u,int v){ to[++tot]=v; nxt[tot]=head[u]; head[u]=tot; }
int dep[100005],f[100005][21];
void dfs(int u,int fa){
dep[u]=dep[fa]+1; f[u][0]=fa;
for(int i=1;i<=20;++i)
f[u][i]=f[f[u][i-1]][i-1];
for(int i=head[u];i;i=nxt[i])
if(to[i]!=fa) dfs(to[i],u);
}
inline int lca(int u,int v){
if(dep[u]>dep[v]) swap(u,v);
for(int i=20;~i;--i)
if(dep[u]<=dep[v]-(1<<i)) v=f[v][i];
if(u==v) return u;
for(int i=20;~i;--i)
if(f[u][i]!=f[v][i]){ u=f[u][i]; v=f[v][i]; }
return f[u][0];
}
int n,q;
int main(){
freopen("inter.in","r",stdin);
freopen("inter.out","w",stdout);
read(n);
for(int i=1;i<n;++i){
int u,v; read(u); read(v);
add(u,v); add(v,u);
}
dfs(1,0);
read(q);
while(q--){
int a,b,c,d;
read(a); read(b); read(c); read(d);
int LCA1=lca(a,b),LCA2=lca(c,d);
if(dep[LCA1]==dep[LCA2]&&LCA1!=LCA2) puts("NO");
else {
if(LCA1>LCA2){ swap(a,c); swap(b,d); swap(LCA1,LCA2); }
int tmp1=lca(a,LCA2),tmp2=lca(b,LCA2);
if(tmp1==LCA2||tmp2==LCA2) puts("YES");
else puts("NO");
}
}
return 0;
}
【jzoj 5853】老大
Description
Input
第一行,一个整数 $ n $ 。
接下来的 $ n-1 $ 行,每行两个数 $ x, y $
Output
一个数,表示最小的最大距离。
Sample Input
输入 1
5
1 2
2 3
3 4
4 5
输入 2
8
1 2
1 3
2 4
2 5
3 6
3 7
1 8
Sample Output
输出 1
1
输出 2
2
Data Constraint
题解
-
$ 60 $ % $ O(n^3) $
$ n^2 $ 枚举两个奖杯位置,再 $ O(n) $ 扫一遍看看每个位置离最近奖杯最远是多少。 -
$ 80 $ % $ O(n^2) $
考虑两个奖杯管辖的区域必定有一个边界,我们枚举这个边界,也就是一条边,
其中一部分是子树,一部分是子树外,我们只要分别求出另外两棵树的直径。 -
树形态随机
期望树的直径很短,两个奖杯都在直径上枚举。 -
$ 100 $ % 二分答案1 $ O(n imes log_n) $
奖杯在直径上,二分答案后取离直径上离端点距离答案的点,遍历 $ check $ 一遍。 -
$ 100 $ % 二分答案2 $ O(n imes log_n ) $
随便提一个节点为根,二分答案,深度最深的节点一定要被照顾到,所以最深的点往上跳答案层即可,
和其距离答案以内的点都删掉,再做一次,
此法可以拓展到 $ k $ 个奖杯,由皮皮轩友情提供。 -
$ 100 $ % 树形 $ DP quad O(n) $
在 $ 80 $ 分的基础上用树形 $ DP $ ,记下每个点向下前三长和向上一格后不回该子树最长的路径长度。
子树内直径是前两长的和与该子树各自子树直径取 $ max $ ,子树外直径是父节点向上一格后不回该子树最长的路径长度,
前两长不进入该子树的向下最长路这三条取前两长加起来与父节点以上的答案取 $ max $
代码
- 代码来自Chevalier
#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<queue>
using namespace std;
int n,d[4000010],v[4000020],pre[4000020],z[4000010],far[4000010];
int tot,head[4000010],ver[4000010],nxt[4000010],l[4000010];
int len,z1[4000010],totz,ans=4000020;
queue<int> q;
void add(int x,int y){
ver[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
int bfs(int s){
int i,x,y;
memset(d,0x3f,sizeof(d));
q.push(s);d[s]=0;
while(q.size()){
x=q.front(); q.pop();
for(i=head[x];i;i=nxt[i])
if(d[ver[i]]==0x3f3f3f3f)
d[ver[i]]=d[x]+1,pre[ver[i]]=x,q.push(ver[i]);
}
for(x=y=1;x<=n;x++) if(d[x]>d[y]) y=x;
return y;
}
int get(){
int p=bfs(1);
pre[p]=0;
p=bfs(p);
return p;
}
int dfs(int x){
int tmp=0;
for(int i=head[x];i;i=nxt[i]){
int y=ver[i];
if(v[y]||z[y])continue;
v[y]=1;
tmp=max(tmp,dfs(y));
}
return tmp+1;
}
int main(){
freopen("ob.in","r",stdin);
freopen("ob.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<n;i++){
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
int root=get();
while(root){
z[root]=1;
z1[++totz]=root;
len++;
l[totz]=len;
root=pre[root];
}
memset(v,0,sizeof v);
for(int i=1;i<=totz;i++){
far[i]=dfs(z1[i]),far[i]--;
if((len%2)&&far[i]==len/2){
printf("%d
",far[i]);
return 0;
}
}
int i=(totz+1)/2,j=i+!(totz%2);
int m=0,ti,tj;
while(i&&j<=totz){
int tmp=0;
tmp=max(tmp,len-l[j]);
tmp=max(tmp,(l[j]-l[i])/2);
tmp=max(tmp,m);
if(tmp<ans)tj=j,ti=i;
ans=min(ans,tmp);
m=max(m,max(far[i],far[j]));
m++;
i--,j++;
}
printf("%d
",ans);
return 0;
}
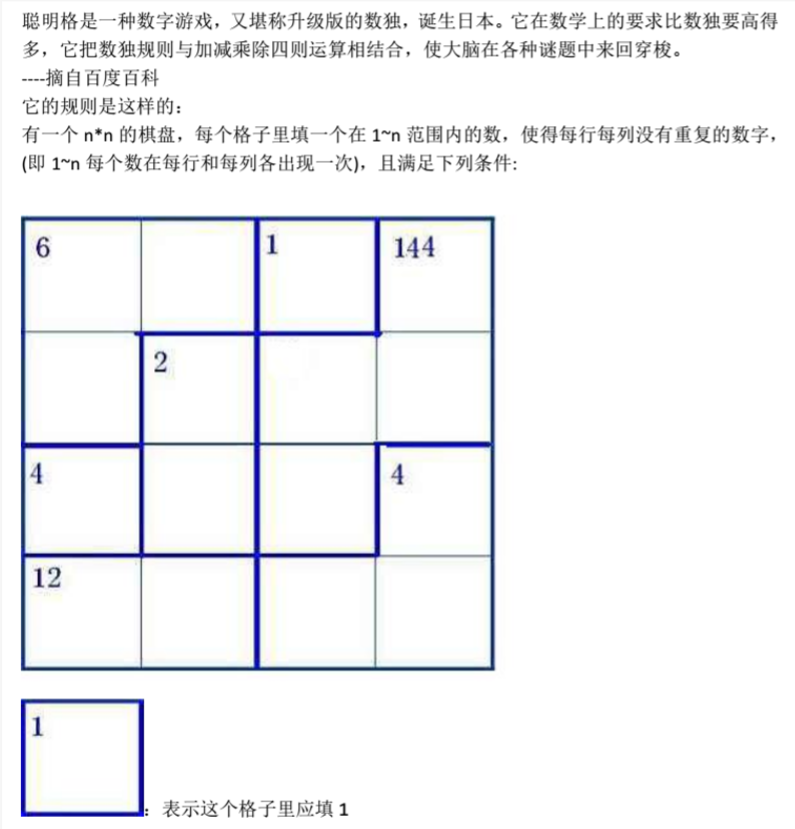
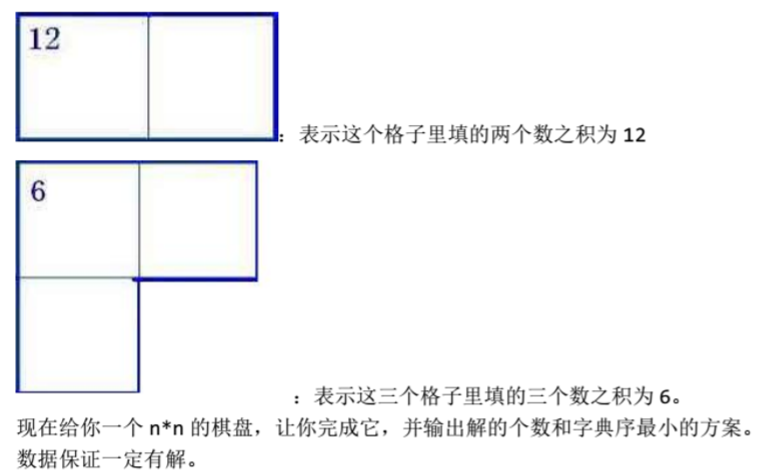
【jzoj 5854】聪明格
Description

Sample Input
输入 1
4
6 6 1 144
6 2 144 144
4 2 144 4
12 12 4 4
输入 2
3
12 12 18
12 12 18
18 18 18
输入 3:
9
32 35 35 42 42 54 54 54 4
32 27 35 576 10 108 108 108 4
9 27 576 576 10 40 40 1008 1008
9 270 576 576 8 14 14 1008 1008
14 270 270 576 8 105 32 8 3
14 4 2688 27 27 105 32 8 10
30 2688 2688 80 6 105 63 63 10
30 2688 126 80 80 24 3 63 9
6 6 126 126 126 24 24 40 40
Sample Output
输出 1
1
2 3 1 4
1 2 4 3
4 1 3 2
3 4 2 1
输出 2
4
1 2 3
2 3 1
3 1 2
输出 3
1
8 1 5 6 7 9 2 3 4
4 3 7 8 5 6 9 2 1
1 9 4 3 2 8 5 6 7
9 5 3 1 8 2 7 4 6
7 6 9 2 1 5 4 8 3
2 4 6 9 3 7 8 1 5
5 7 8 4 6 3 1 9 2
6 8 2 5 4 1 3 7 9
3 2 1 7 9 4 6 5 8
Data Constraint
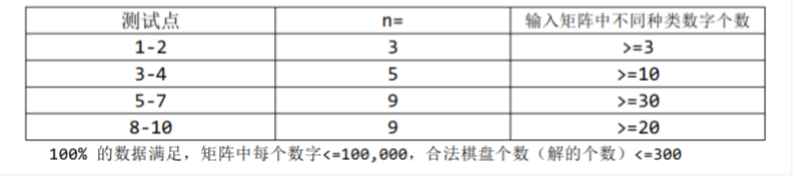
题解
-
20%: $ n=3 ,只要按顺序枚举棋盘上每个数字是多少,枚举完了之后 $ n^2 $ 判断一下是否可行。
时间复杂度:$ (3^9) imes (9^2) $ -
40%: 在顺序枚举的基础上每行每列开一个哈希表,记录每行每列哪些数字已经出现过了, 搜索时跳过即可。
-
70%: 在 40%的基础上记录每个连通块当前填的数字之积,然后判断当前填的数字是否可行。
-
100%:我们考虑是连通块内数字之积的约束性比每行每列不重复要大得多,所以每次尽量将一个连通块填满。
我们可以将所有连通块按连通块数字个数排序,
连通块大小相同按 $ 1-9 $ 因数个数排序(这样能使选择的余地尽可能小),然后按顺序将每个连通块填满即可。
代码
- 代码来自Akoasm
#include <bits/stdc++.h>
using namespace std;
const int maxn=15;
int _cnt[maxn*maxn],sum=0,n,tot=0,cnt=0;
int a[maxn][maxn],Cntr[maxn][maxn],p[maxn*maxn][maxn],mul[maxn*maxn];
int nxt[4][2],mark[maxn][maxn],ans[maxn][maxn],d[maxn*maxn][2],h[maxn][maxn],l[maxn][maxn],hlim[maxn][maxn],llim[maxn][maxn],v[maxn][maxn],c[maxn][maxn][maxn];
inline void dfs(int x,int y)
{
Cntr[x][y]=tot;
_cnt[tot]++;
for (int i=0;i<=3;i++)
{
int tx=nxt[i][0]+x,ty=nxt[i][1]+y;
if (a[tx][ty]==a[x][y]&&!Cntr[tx][ty]) dfs(tx,ty);
}
}
inline bool check()
{
for (int i=1;i<=tot;i++) if (mul[i]!=1) return 0;
return 1;
}
inline void Memcpy()
{
for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) ans[i][j]=mark[i][j];
}
inline void judge()
{
int flag=-999;
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++) if (ans[i][j]<mark[i][j])
{
flag=0;
break;
}else if (ans[i][j]>mark[i][j])
{
flag=1;
break;
}
if (flag!=-999) break;
}
if (flag) Memcpy();
}
inline void dfs(int x)
{
if (x==cnt+1)
{
sum++;
if (!check()) return;
if (sum==1) Memcpy();else judge();
return;
}
int tx=d[x][0],ty=d[x][1],tmp=Cntr[tx][ty];
if (_cnt[tmp]==1)
{
int v=mul[tmp];
if (v<=n&&v>=1&&!hlim[tx][v]&&!llim[ty][v])
{
hlim[tx][v]=1;
llim[ty][v]=1;
mul[tmp]=1;
mark[tx][ty]=v;
dfs(x+1);
hlim[tx][v]=0;
llim[ty][v]=0;
mul[tmp]=v;
}
}else
for (int i=1;i<=n;i++)
{
if (p[tmp][i]&&!hlim[tx][i]&&!llim[ty][i]&&mul[tmp]%i==0)
{
mul[tmp]=mul[tmp]/i;
hlim[tx][i]=1;
llim[ty][i]=1;
mark[tx][ty]=i;
_cnt[tmp]--;
dfs(x+1);
mul[tmp]=mul[tmp]*i;
hlim[tx][i]=0;
llim[ty][i]=0;
_cnt[tmp]++;
}
}
}
inline void init() {
nxt[0][0]=1;
nxt[1][0]=-1;
nxt[2][1]=1;
nxt[3][1]=-1;
}
int main()
{
freopen("kenken.in","r",stdin);
freopen("kenken.out","w",stdout);
init();
scanf("%d",&n);
for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) scanf("%d",&a[i][j]);
for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) if (!Cntr[i][j])
{
tot++;
for (int k=2;k<=n;k++) if (a[i][j]%k==0)
{
int r,cc;
for (r=k,cc=1;a[i][j]%r==0;r=r*k,cc++) p[tot][k]=cc;
}else p[tot][k]=0;
p[tot][1]=n*n;
mul[tot]=a[i][j];
dfs(i,j);
}
for (int i=1;i<=n;i++)
{
for (int j=1;j<=n;j++)
{
if (Cntr[i][j]!=Cntr[i][j+1])
{
int tmp=Cntr[i][j];
for (int k=1;k<=n;k++) h[i][k]=h[i][k]+p[tmp][k];
}
if (Cntr[j][i]!=Cntr[j+1][i])
{
int tmp=Cntr[j][i];
for (int k=1;k<=n;k++) l[i][k]=l[i][k]+p[tmp][k];
}
int tmp=Cntr[i][j];
for (int k=1;k<=n;k++) c[i][j][k]=p[tmp][k];
}
}
for (int i=1;i<=n;i++) for (int j=1;j<=n;j++) if (!v[i][j])
{
cnt++;
d[cnt][0]=i;
d[cnt][1]=j;
}
for (int i=1;i<=cnt;i++)
{
for (int j=i+1;j<=cnt;j++) if (a[d[i][0]][d[i][1]]>a[d[j][0]][d[j][1]])
{
swap(d[i],d[j]);
}
}
dfs(1);
printf("%d
",sum);
for (int i=1;i<=n;i++)
{
for (int j=1;j<n;j++) printf("%d ",ans[i][j]);
printf("%d
",ans[i][n]);
}
return 0;
}





