Couple Trees
时间限制: 2000ms
单点时限: 2000ms
内存限制: 256MB
描述
"Couple Trees" are two trees, a husband tree and a wife tree.
They are named because they look like a couple leaning on each other.
They share a same root, and their branches are intertwined.
In China, many lovers go to the couple trees. Under the trees, lovers wish to be accompanied by a lifetime.
Ada and her boyfriend Asa came to the couple trees as well.
They were very interested in the trees. They were all ACMers,
so after careful observation, they found out that these two trees could be considered as two "trees" in graph theory.
These two trees shared $ N $ vertices which were labeled $ 1 $ to $ N $ ,
and they all had exactly $ N $ vertices. Vertices $ 1 $ was the root of both trees.
Ada and Asa wanted to know more about the trees' rough bark, so each of them put one thumb at a vertices.
Then they moved their thumbs towards the root. Ada moved along the wife tree,
and Asa moved along the husband tree.
Of course, they could moved at different speed.
At that moment, a thought suddenly came to Ada's mind:
their thumbs may meet before the root. Which one was the earliest possible meeting vertex?
And how many vertices would Ada and Asa encounter on the way to the meeting vertex?
输入
The input consists of no more than 8 test cases.
For each test case:
The first line contains two integers, $ N $ and $ M $ ,
indicating the number of vertices and the number of queries.$ (1≤N,M≤100,000) $
The next line contains $ N−1 $ integers. It describes the structure of wife tree in this way:
If the $ i^{th} $ integer is $ k $ , it means that the vertex labeled $ k $ is the father vertex of the vertex labeled $ (i+1) $ .
It's guaranteed that a vertex $ X $ 's father vertex can't have a larger label than $ X $ does.
The next line describes the husband tree in the same way.
Then next $ M $ lines describe the queries.
Each line contains two integers $ X_i $ and $ Y_i $ .
Let $ K_i $ be the earliest possible meeting vertex of the ith query ( $ K_0 $ is defined as $ 0 $ ).
In the $ i^{th} $ query, Ada's thumb was put at the vertex labeled $ ( X_i+K_i−1) quad mod quad N + 1 $
and Asa's thumb was put at the vertex labeled $ (Y_i+K_i−1) quad mod quad N + 1.(1≤X_i,Y_i≤N) $ at the beginning.
输出
For each test case:
Output the answer for each query in a single line.
The answer contains three integers: the earliest possible meeting vertex,
the number of the vertices Ada will encounter and the number of the vertices Asa will encounter
(including the starting vertex and the ending vertex).
In particular, if they put their thumb at the same vertex at first, the earliest possible meeting vertex should be the starting vertex.
提示
In the first test case:
The wife tree is like this:
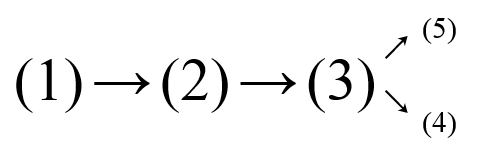
The husband tree is like this:
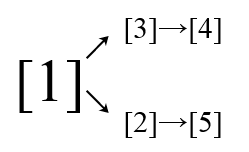
The query is $ (5)[4] $ , and they may meet at { $ 1,3 $ }, so the earliest one is $ 3 $ .
In the second test case:
The wife tree is like this:
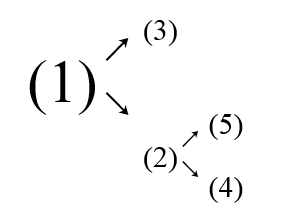
The husband tree is like this:
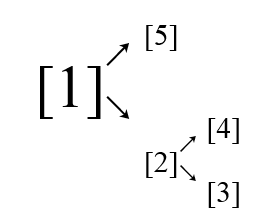
The first query is $ (1)[4] $ , the second query is $ (2)[1] $ , and the last one is $ (5)[2] $ .
For the first query, they may only meet at 1.
For the second query, they may only meet at 1.
For the third query, they may meet at {$ 1,2 $ } , the earliest one is $ 2 $ .
样例输入
5 1
1 2 3 3
1 1 3 2
4 3
5 3
1 1 2 2
1 2 2 1
5 3
5 4
3 5
5 3
1 1 2 2
1 2 3 1
1 4
1 1
3 4
样例输出
3 2 2
1 1 3
1 2 1
2 2 1
1 2 2
3 1 1
2 1 2
题目大意
-
给出两棵树,它们共用 $ N $ 个节点,但边地连接情况不同。
-
给出 $ M $ 个询问,每次询问给出分别属于两棵树地点 $ x,y $ ,求它们的 $ lca $ 。
-
保证 $u ightarrow v $ 的同时,$ u $ 比 $ v $ 小
题解
-
求出第二棵树的 $ DFS $ 序,使用标记永久化的可持久化线段树维护
-
$ DFS $ 遍历第一棵树,每递归进入一个点 $ x $ ,就在第二棵树 $ DFS $ 序上覆盖 $ x $ 对应的区间
-
离线考虑涉及 $ x $ 的询问,答案就是 $ y $ 被最新覆盖的值
-
从 $ x $ 回溯时,撤销区间覆盖
其实我没看懂上面的lyd的题解,树上倍增不是更简单吗?
-我们对两棵树分别进行一边dfs,在跑它们的lca时,考虑到单调性的问题,
我们尝试用较大的节点去向上找到较大的节点就可以了。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
#define maxn 100010
vector<int>e1[maxn],e2[maxn];
int n,m,f1[maxn][21],f2[maxn][21],dep1[maxn],dep2[maxn];
void dfs1(int u){
for(int i=0;i<e1[u].size();++i)
if(e1[u][i]!=f1[u][0]){
int v=e1[u][i];
f1[v][0]=u;
for(int j=1;(1<<j)<=v;++j)
f1[v][j]=f1[f1[v][j-1]][j-1];
dfs1(v);
}
}
void dfs2(int u){
for(int i=0;i<e2[u].size();++i)
if(e2[u][i]!=f2[u][0]){
int v=e2[u][i];
f2[v][0]=u;
for(int j=1;(1<<j)<=v;++j)
f2[v][j]=f2[f2[v][j-1]][j-1];
dfs2(v);
}
}
inline int lca(int u,int v){
int stp1=1,stp2=1;
while(u!=v){
if(u<v){
for(int i=20;~i;--i)
if(u<f2[v][i]&&f2[v][i]!=-1){ v=f2[v][i]; stp2+=(1<<i); }
stp2+=1; v=f2[v][0];
} else {
for(int i=20;~i;--i)
if(v<f1[u][i]&&f1[u][i]!=-1){ u=f1[u][i]; stp1+=(1<<i); }
stp1+=1; u=f1[u][0];
}
}
printf("%d %d %d
",u,stp1,stp2);
return u;
}
int main(){
while(scanf("%d %d",&n,&m)!=EOF){
for(int i=1;i<=n;++i){ e1[i].clear(); e2[i].clear(); }
memset(f1,-1,sizeof(f1));
memset(f2,-1,sizeof(f2));
for(int u,i=2;i<=n;++i){
scanf("%d",&u);
e1[u].push_back(i);
}
for(int u,i=2;i<=n;++i){
scanf("%d",&u);
e2[u].push_back(i);
}
dfs1(1); dfs2(1);
int lst=0;
while(m--){
int u,v;
scanf("%d %d",&u,&v);
u=(u+lst)%n+1;
v=(v+lst)%n+1;
lst=lca(u,v);
}
}
return 0;
}