决策树

import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import sys
import os  
from IPython.display import Latex
os.environ["PATH"] += os.pathsep + r'C:UsersYTODesktopgraphvizGraphvizin'

csv下载地址: https://www.kaggle.com/c/titanic/data

train = pd.read_csv(r".	itanic	rain.csv")
test = pd.read_csv(r".	itanic	est.csv")

train = train[train['Embarked'].notna()] # 丢掉Embarked为空的数据
train = train[train['Age'].notna()] # 丢掉Embarked为空的数据
combine = [train, test]

for df in combine:
    df["Sex"] = df['Sex'].map({"male": 1, "female": 0}).astype(int)
    df["Embarked"] = df['Embarked'].map({"C": 0, "S": 1, "Q": 2}).astype(int)

train.count()

PassengerId    712
Survived       712
Pclass         712
Name           712
Sex            712
Age            712
SibSp          712
Parch          712
Ticket         712
Fare           712
Cabin          183
Embarked       712
dtype: int64

cols = ["Sex", "Age","Embarked","Pclass"] # 'Fare'
X_train = train[cols]
X_test = test[cols]
Y_train = train[["Survived"]]
logreg = DecisionTreeClassifier(max_depth=3,criterion='entropy')
logreg.fit(X_train, Y_train.values.ravel())
logreg.score(X_train, Y_train)

0.7991573033707865

# 下面一坨代码是用来生成树图，不用理解
# 第一步是安装graphviz。下载地址在：http://www.graphviz.org/。如果你是linux，可以用apt-get或者yum的方法安装。
# 如果是windows，就在官网下载msi文件安装。无论是linux还是windows，装完后都要设置环境变量，将graphviz的bin目录加到PATH，
# 比如我是windows，将C:/Program Files (x86)/Graphviz2.38/bin/加入了PATH
# 第二步是安装python插件graphviz： pip install graphviz
# 第三步是安装python插件pydotplus。这个没有什么好说的: pip install pydotplus
# 这样环境就搭好了，有时候python会很笨，仍然找不到graphviz，这时，可以在代码里面加入这一行：
# os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
import pydotplus
import graphviz
from IPython.display import Image  
dot_data = tree.export_graphviz(logreg, out_file=None, 
                         feature_names=cols,  
                         class_names=['Not Survived','Survived'],  
                         filled=True, rounded=True,  
                         special_characters=True)  
graph = graphviz.Source(dot_data)
graph
# graph.render("logreg") # 将树图保存成pdf,可以打开当前目录去看

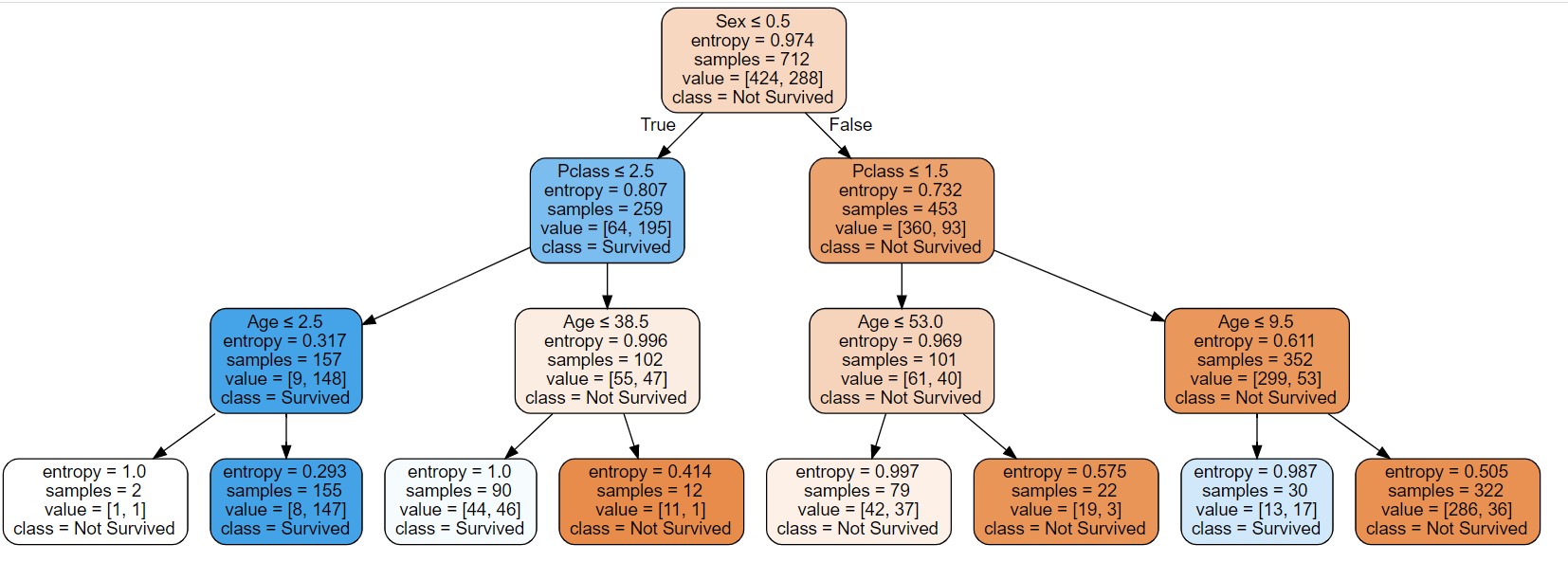
# 参数: criterion  有2个选择 : {"gini", "entropy"}，default="gini"
# gini系数算法：
Latex(r"$Gini(p)= sum_{k=1}^K p_{k} (1-p_{k}) =1- sum_{k=1}^K p_{k}^2 $")

$Gini(p)= sum_{k=1}^K p_{k} (1-p_{k}) =1- sum_{k=1}^K p_{k}^2 $

# 转成函数就是
def get_gini(li):
    sum_li = sum(li)
    p_li = [i / sum_li for i in li]
    res = 1 - sum([p ** 2 for p in p_li])
    return res

print(get_gini([549,340]))

0.4723650263627057

# 信息熵算法：
Latex(r"$Entropy(p)= - sum_{k=1}^K p_{k} log_{2}p_{k} $")

$Entropy(p)= - sum_{k=1}^K p_{k} log_{2}p_{k} $

# 转成函数就是
def get_entropy(li):
    sum_li = sum(li)
    p_li = [i / sum_li for i in li]
    res = - sum([p * np.log2(p) for p in p_li])
    return res

print(get_entropy([64, 195]))

0.806656120963874

# 决策树的特征选择：https://zhuanlan.zhihu.com/p/30755724