Polya计数

Let it Bead

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 5365		Accepted: 3585

Description

"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It's a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced. 

A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.

Input

Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.

Output

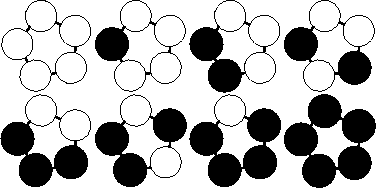For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.

Sample Input

1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0

Sample Output

1
2
3
5
8
13
21

/*
poj 2409 Polya模板题

旋转：
L = sum(k^Ci)/n(i = 0,1.....n-1)      求出每次旋转i位的和
顺时针旋转i格的置换中,循环的个数为GCD(n,i),长度为n/GCD(n,i).
so Ci = GCD(n,i)

翻转：
当n为偶数时,n/2个的置换Ci = n/2； n/2个的置换Ci = n/2-1
当n为奇数时,n个置换Ci = n/2+1

hhh-2016-04-19 10:06:23
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;

ll gcd(ll a, ll b) {
    return b ? gcd(b, a%b) : a;
}
ll pow(ll a, ll b)
{
    ll res = 1;
    while(b)
    {
        if(b&1) res *= a;
        a = a*a;
        b >>= 1;
    }
    return res;
}

ll polya(ll n,ll k)
{
    ll ans = 0;
    for(int i = 1; i <= n; i++)
    {
        ans += pow(k,gcd(n,i));
    }

    if(n & 1)
        ans  += pow(k,n/2+1)*n;
    else
    {
        ans += pow(k,n/2)*(n/2);
        ans += pow(k,n/2+1)*(n/2);
    }
    return ans/(n*2);
}

int main()
{
    ll n,c;
    while(scanf("%I64d%I64d",&c,&n) != EOF)
    {
        if(!n && !c)
            break;
        printf("%I64d
",polya(n,c));
    }
    return 0;
}

　　

Necklace of Beads

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 7525		Accepted: 3132

Description

Beads of red, blue or green colors are connected together into a circular necklace of n beads ( n < 24 ). If the repetitions that are produced by rotation around the center of the circular necklace or reflection to the axis of symmetry are all neglected, how many different forms of the necklace are there? 

Input

The input has several lines, and each line contains the input data n. 
-1 denotes the end of the input file. 

Output

The output should contain the output data: Number of different forms, in each line correspondent to the input data.

Sample Input

4
5
-1

Sample Output

21
39

/*
poj 1286 polya(euler优化)

依旧是模板题，只是在上面加了优化
优化：(黑书)
以前都是直接枚举i来求解。  但是可以考虑通过枚举循环节的长度L,然后计算有多少个i
L = n/(GCD(n,i))  ->   GCD(n,i) = n/L
不妨设 a = n/L = GCD(n,i) , 不妨设 i = a*t  -> GCD(n,i) = GCD(a*L,a*t) = a
所以只有 GCD(L,t) = 1是才行。  0 ≤ i <n --->   0 ≤ t < L(n/a)
即小于L且与L互质的个数,这个用欧拉函数解决

hhh-2016-04-19 11:14:49
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;

ll euler(ll n)
{
    ll ans = n;
    for(int i = 2;i*i <= n;i++)
    {
        if(n % i == 0)
        {
            ans -= ans/i;
            while(n % i == 0)
            {
                n /= i;
            }
        }
    }
    if(n > 1) ans -= ans/n;
    return ans;
}

ll gcd(ll a, ll b) {
    return b ? gcd(b, a%b) : a;
}
ll Pow(ll a, ll b)
{
    ll res = 1;
    while(b)
    {
        if(b&1) res *= a;
        a = a*a;
        b >>= 1;
    }
    return res;
}

ll polya(ll n,ll k)
{
    ll ans = 0;
    for(ll i = 1; i <= n; i++)
    {
        if(n % i == 0)   //枚举循环节的长度
        ans += Pow(k,i)*euler(n/i);
    }

    if(n & 1)
        ans  += Pow(k,n/2+1)*n;
    else
    {
        ans += Pow(k,n/2)*(n/2);
        ans += Pow(k,n/2+1)*(n/2);
    }
    return ans/(n*2);
}

int main()
{
    ll n;
    while(scanf("%I64d",&n) != EOF)
    {
        if(n == -1)
            break;
        if(n == 0)
            printf("0
");
        else
        printf("%I64d
",polya(n,3));
    }
    return 0;
}

　　

Invoker

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 122768/62768 K (Java/Others)
Total Submission(s): 1426    Accepted Submission(s): 610

Problem Description

On of Vance's favourite hero is Invoker, Kael. As many people knows Kael can control the elements and combine them to invoke a powerful skill. Vance like Kael very much so he changes the map to make Kael more powerful. 

In his new map, Kael can control n kind of elements and he can put m elements equal-spacedly on a magic ring and combine them to invoke a new skill. But if a arrangement can change into another by rotate the magic ring or reverse the ring along the axis, they will invoke the same skill. Now give you n and m how many different skill can Kael invoke? As the number maybe too large, just output the answer mod 1000000007.

 

Input

The first line contains a single positive integer T( T <= 500 ), indicates the number of test cases.
For each test case: give you two positive integers n and m. ( 1 <= n, m <= 10000 )

 

Output

For each test case: output the case number as shown and then output the answer mod 1000000007 in a line. Look sample for more information.

 

Sample Input

2 3 4 1 2

 

Sample Output

Case #1: 21 Case #2: 1

/*
HDU 3923 Ploya定理+逆元

裸Polya计数,只是在后面求个逆元即可

hhh-2016-04-19 11:40:12
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson  (i<<1)
#define rson  ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;
const int mod = 1000000007;
ll euler(ll n)
{
    ll ans = n;
    for(int i = 2;i*i <= n;i++)
    {
        if(n % i == 0)
        {
            ans -= ans/i;
            while(n % i == 0)
            {
                n /= i;
            }
        }
    }
    if(n > 1) ans -= ans/n;
    return ans%mod;
}

ll Pow(ll a, ll b)
{
    ll res = 1;
    a %= mod;
    while(b)
    {
        if(b&1) res =res*a%mod;
        a = a*a%mod;
        b >>= 1;
    }
    return res%mod;
}

ll polya(ll n,ll k)
{
    ll ans = 0;
    for(ll i = 1; i <= n; i++)
    {
        if(n % i == 0)   //枚举循环节的长度
        ans =(ans+Pow(k,i)*euler(n/i)%mod)%mod;
    }

    if(n & 1)
        ans =(ans+Pow(k,n/2+1)*n%mod)%mod;
    else
    {
        ans = (ans+Pow(k,n/2)*(n/2)%mod)%mod;
        ans = (ans+Pow(k,n/2+1)*(n/2)%mod)%mod;
    }
   ll t = Pow(n*2,mod-2);     //求逆元
    return ans*t%mod;
}

int main()
{
    ll n,c;
    int T,cas = 1;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%I64d%I64d",&c,&n);
        printf("Case #%d: ",cas++);
        printf("%I64d
",polya(n,c));
    }
    return 0;
}

DIY Cube

Time Limit: 2000/2000 MS (Java/Others)    Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 637    Accepted Submission(s): 313

Problem Description

Mr. D is interesting in combinatorial enumeration. Now he want to find out the number of ways on painting the vertexes of a cube. Suppose there are C different colors and two paintings are considered the same if they can transform from one to another by rotation.

 

Input

There are multiple test cases in the input, the first line of input contains an integer denoting the number of test cases.
For each test case, there are only one integer C, denoting the number of colors. (1 <= C <= 1000000000)

 

Output

For each test case, output the the number of painting ways. And if the number is equal or larger than 10¹⁵, output the last 15 digits.

 

Sample Input

3 1 2 112

 

Sample Output

Case 1: 1 Case 2: 23 Case 3: 031651434916928

//hdu 3547 用C种颜色对正方形的八个顶点染色
//如果用1234表示顶面   5678表示底面
//1.绕着相互对立的两个面旋转，有90度，180度，270度，所以总共有3*3=9种情况。 
//    绕90 or 270.  {1 2 3 4} {5,6,7,8} 2个循环节   总共有6中情况
//    绕180   {1,3}{2,4}{5,7}{6,8} 4个循环节   共有3种情况
//2.绕着相互对立的两个边旋转，有180度这样，所以总共有6*1=6种。
//    {1,7}{2,8}{3,4}{5,6} 4个循环节
//3.绕着对角点旋转，有120度，240度这样，所以总共有4*2=8种。 
//    {2,5,7}{1,3,8}{6}{4} 4个循环节
//4.不动，有一种。    {1}{2}{3}{4}{5}{6}{7}{8} 8个循环节
//假设有C中颜色      则共有C^8 + 17*C^4 + 6*C^2
import java.math.BigInteger;
import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		Scanner cin = new Scanner(System.in);
		int T = cin.nextInt();
		int cas = 1;
		while(T>0){
			BigInteger c = cin.nextBigInteger();
        
        BigInteger t1 = c.pow(8);
        BigInteger t2 = c.pow(4);
        BigInteger t3 = c.pow(2);
//        System.out.println("t1:"+t1);
//        System.out.println("t2:"+t2);
//        System.out.println("t3:"+t3);
        t2 = t2.multiply(BigInteger.valueOf(17));
        t3 = t3.multiply(BigInteger.valueOf(6));

        BigInteger ans = t1.add(t2).add(t3);
        String tans = ans.divide(BigInteger.valueOf(24)).toString();
        int len = tans.length();
        System.out.print("Case " + cas+": ");
        if(len <= 15)
        System.out.println(tans);
        else
        	System.out.println(tans.substring(len-15));
        cas++;
        T--;
		}
		}
}