星星之火,可以燎原
细节的地方慢慢补充,欢迎提出问题,私聊/留言均可
A. 跳跳棋
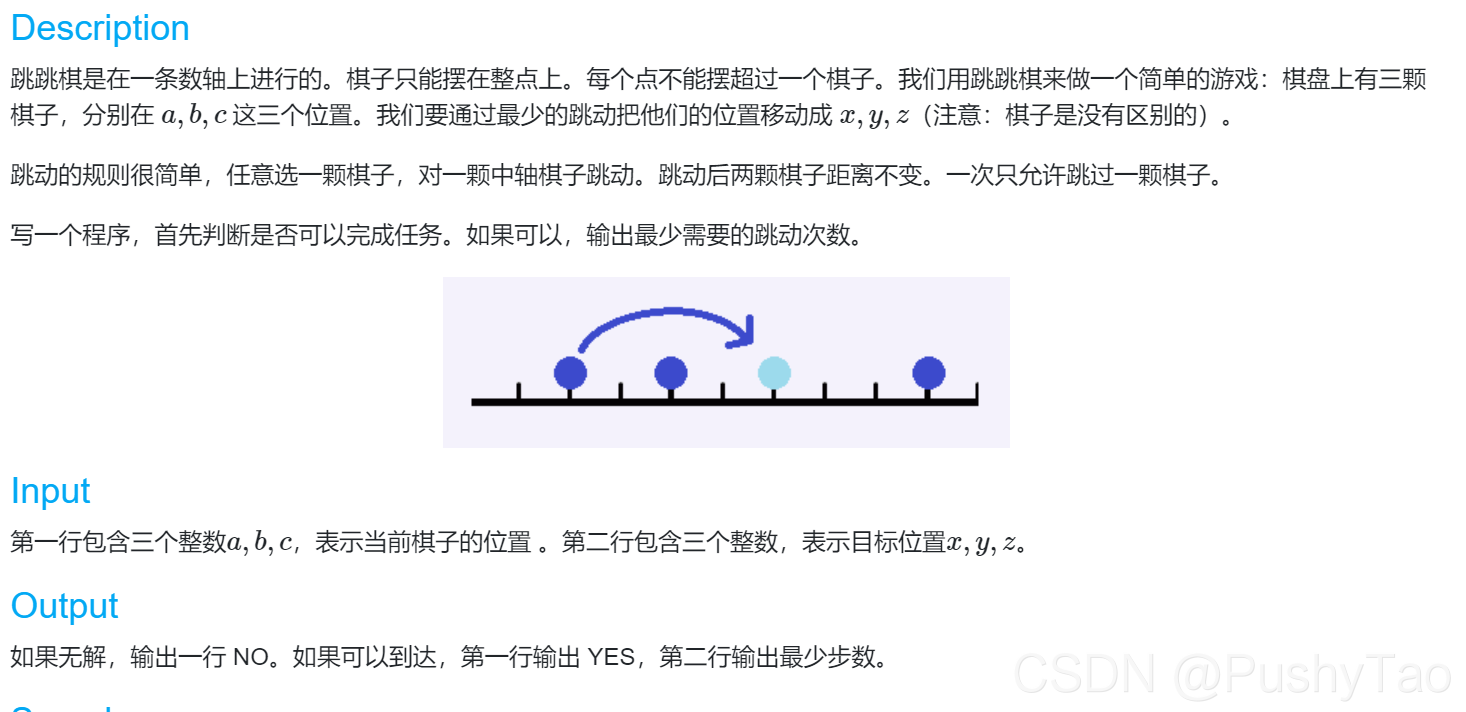
较难
struct node
{
int a, b, c;
friend bool operator != (node a, node b)
{
if(a.a != b.a || a.b != b.b || a.c != b.c) return true;
return false;
}
void srt()
{
int temp[] = {a, b, c};
sort(temp, temp + 3);
a = temp[0], b = temp[1], c = temp[2];
}
} pnt1, pnt2;
node getRoot(node pnt, int &cnt)
{
/// dis1 == dis2 -> return pnt ok;
while(pnt.c - pnt.b != pnt.b - pnt.a)
{
int dis1 = pnt.b - pnt.a;
int dis2 = pnt.c - pnt.b;
if(dis1 < dis2)
{
int t = dis2 / dis1;
if(dis2 % dis1 == 0) -- t;
pnt.a += t * dis1;
pnt.b += t * dis1;
cnt += t;
}
else
{
int t = dis1 / dis2;
if(dis1 % dis2 == 0) -- t;
pnt.c -= t * dis2;
pnt.b -= t * dis2;
cnt += t;
}
}
return pnt;
}
node moveUp(node pnt, int cnt)
{
while(pnt.b - pnt.a != pnt.c - pnt.b && cnt)
{
int dis1 = pnt.b - pnt.a;
int dis2 = pnt.c - pnt.b;
if(dis1 < dis2)
{
int t = dis2 / dis1;
if(dis2 % dis1 == 0) -- t;
if(cnt < t) t = cnt;
pnt.a += t * dis1;
pnt.b += t * dis1;
cnt -= t;
}
else
{
int t = dis1 / dis2;
if(dis1 % dis2 == 0) -- t;
if(cnt < t) t = cnt;
pnt.c -= t * dis2;
pnt.b -= t * dis2;
cnt -= t;
}
}
return pnt;
}
int main()
{
cin >> pnt1.a >> pnt1.b >> pnt1.c;
cin >> pnt2.a >> pnt2.b >> pnt2.c;
pnt1.srt(), pnt2.srt();
int cnt1 = 0, cnt2 = 0;
node root1 = getRoot(pnt1, cnt1);
node root2 = getRoot(pnt2, cnt2);
if(root1 != root2)
{
puts("NO");
return 0;
}
// puts("OK");
if(cnt1 < cnt2) swap(pnt1, pnt2), swap(cnt1, cnt2);
int l = 0, r = 1000000000;
pnt1 = moveUp(pnt1, cnt1 - cnt2);
int ans = 0;
// puts("OK");
while(l <= r)
{
int mid = l + r >> 1;
// cout << l << " " << r <<endl;
if(!(moveUp(pnt1, mid) != moveUp(pnt2, mid)))
{
r = mid - 1;
ans = mid;
}
else l = mid + 1;
// puts("end of while");
}
puts("YES");
cout << ans * 2 + cnt1 - cnt2 << endl;
return 0;
}
/**
**/
B. 聚会

板子题
n个城市之间的距离是1
所以在求lca的过程中,深度的差值即可表示为距离
两个点a,b,之间的lca为_lca
那么这两个点之间的距离为dep[a] - dep[_lca] + dep[b] - dep[_lca],-> dep[a] + dep[b] - dep[_lca] * 2
这仅仅是两个点的情况
三个点的情况略有不同:
若三个点在同一棵子树上:
若三个点在同一条链上:
所以说我们要考虑任意两点之间的关系,然后求两次lca,第一次的lca即为可能的答案位置,最终答案要考虑所有情况中花费最小的那个
int n,m;
int root;
int head[maxn];
struct node {
int u;
int v;
int w;
int next;
} e[maxn];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
int lg[maxn];
int cnt = 0;
void init() {
memset(head,-1,sizeof head);
}
void add(int u,int v) {
e[cnt].u = u;
e[cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur,int rt) {
fa[cur][0] = rt,dep[cur] = dep[rt] + 1;/// the depth of the current node changed
for(int i=1; i <= lg[dep[cur]]; i++) {
fa[cur][i] = fa[fa[cur][i-1]][i-1];
}
for(int i=head[cur]; ~i; i = e[i].next) { /// visit all linked nodes
if(e[i].v != rt) dfs(e[i].v,cur);
}
}
void cal() {
for(int i=1; i<=n; i++) {
lg[i] = lg[i-1] + (1 << lg[i-1] == i);/// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x,int y) {
if(dep[x] < dep[y]) swap(x,y);
while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y) return y;
/// big -> small
for(int k = lg[dep[x]] - 1; k >= 0; k --) {
if(fa[x][k] != fa[y][k]) {
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int main() {
cin >> n >> m;
cal();
init();
for(int i=1; i<n; i++) {
int u = read,v = read;
add(u,v);
add(v,u);
}
ll ans = inf,dis;
int pos = 0;
int lca1,lca2;
dfs(1,0);
for(int i=1; i<=m; i++) {
ans = inf;
int x = read,y = read,z = read;
lca1 = lca(x,y);
dis = dep[x] + dep[y] - 2 * dep[lca1];
lca2 = lca(lca1,z);
dis += dep[lca1] + dep[z] - 2 * dep[lca2];
if(dis < ans) {
ans = dis;
pos = lca1;
}
// debug(lca1);
// debug(dis);
swap(x,z);
lca1 = lca(x,y);
dis = dep[x] + dep[y] - 2 * dep[lca1];
lca2 = lca(lca1,z);
dis += dep[lca1] + dep[z] - 2 * dep[lca2];
if(dis < ans) {
ans = dis;
pos = lca1;
}
swap(y,z);
lca1 = lca(x,y);
dis = dep[x] + dep[y] - 2 * dep[lca1];
lca2 = lca(lca1,z);
dis += dep[lca1] + dep[z] - 2 * dep[lca2];
if(dis <ans) {
ans = dis;
pos = lca1;
}
printf("%d %lld
",pos,ans);
}
return 0;
}
/**
6 4
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
2 4 4
6 6 6
6 2
1 2
2 3
2 4
4 5
5 6
4 5 6
6 3 1
**/
C. 祖孙询问
板子题
求两点之间的lca,如果lca与其中一点相同,输出对应的值,反之输出0
int n,m;
int root;
int head[maxn];
struct node{
int u;
int v;
int next;
}e[maxn];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
int lg[maxn];
int cnt = 0;
void init(){
memset(head,-1,sizeof head);
}
void add(int u,int v){
e[cnt].u = u;
e[cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur,int rt){
fa[cur][0] = rt,dep[cur] = dep[rt] + 1;/// the depth of the current node changed
for(int i=1;i <= lg[dep[cur]];i++){
fa[cur][i] = fa[fa[cur][i-1]][i-1];
}
for(int i=head[cur];~i;i = e[i].next){/// visit all linked nodes
if(e[i].v != rt) dfs(e[i].v,cur);
}
}
void cal(){
for(int i=1;i<=n;i++){
lg[i] = lg[i-1] + (1 << lg[i-1] == i);/// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x,int y){
if(dep[x] < dep[y]) swap(x,y);
while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y) return y;
/// big -> small
for(int k = lg[dep[x]] - 1;k >= 0;k --){
if(fa[x][k] != fa[y][k]){
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int main() {
cin >> n;
cal();
init();
for(int i=1;i<=n;i++){
int x = read,y = read;
if(y == -1) {
root = x;
continue;
}
add(x,y);
add(y,x);
}
dfs(root,0);
cin >> m;
for(int i=1;i<=m;i++){
int x = read,y = read;
int _lca = lca(x,y);
if(_lca == x) puts("1");
else if(_lca == y) puts("2");
else puts("0");
}
return 0;
}/// ac_code
/**
**/
D. Dis

板子题
考虑在更新depth的时候,顺便更新一下两点之间的距离,(在题目中如果说任意两点之间的距离为1的情况,dis可以用depth代替)
typedef pair<int,int> PII;
int n,m;
int root;
int head[maxn];
struct node {
int u;
int v;
int w;
int next;
} e[maxn];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
ll dis[maxn];
int lg[maxn];
int cnt = 0;
map<PII,int> mp;
void init() {
memset(head,-1,sizeof head);
}
void add(int u,int v,int w) {
e[cnt].u = u;
e[cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur,int rt) {
fa[cur][0] = rt,dep[cur] = dep[rt] + 1;/// the depth of the current node changed
dis[cur] = dis[rt] + mp[ {rt,cur}];
for(int i=1; i <= lg[dep[cur]]; i++) {
fa[cur][i] = fa[fa[cur][i-1]][i-1];
}
for(int i=head[cur]; ~i; i = e[i].next) { /// visit all linked nodes
if(e[i].v != rt) dfs(e[i].v,cur);
}
}
void cal() {
for(int i=1; i<=n; i++) {
lg[i] = lg[i-1] + (1 << lg[i-1] == i);/// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x,int y) {
if(dep[x] < dep[y]) swap(x,y);
while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y) return y;
/// big -> small
for(int k = lg[dep[x]] - 1; k >= 0; k --) {
if(fa[x][k] != fa[y][k]) {
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int main() {
cin >> n >> m;
cal();
init();
for(int i=1; i<n; i++) {
int u = read,v = read,w = read;
mp[{u,v}] = mp[{v,u}] = w;
add(u,v,w);
add(v,u,w);
}
dfs(1,0);
for(int i=1; i<=m; i++) {
int x = read,y = read;
int _lca = lca(x,y);
ll ans = dis[x] + dis[y] - 2 * dis[_lca];
printf("%lld
",ans);
}
return 0;
}
/**
2 2
1 2 100
1 2
2 1
**/
E. 次小生成树(严格次小生成树)

难
切掉这个题需要掌握:dfs技巧 + lca + 倍增 + 维护次小边权 + 最小生成树
这个题写下来之后会有很大提高,而且会改掉写代码开内存的坏习惯
int n, m;
struct node {
ll u, v, w;
ll nex;
} e[maxn << 1];
int cnt;
int head[maxn << 1];
void init() {
cnt = 0;
for (int i = 1; i <= 2 * n; i++) {
head[i] = -1;
}
}
void add(ll u, ll v, ll w) {
e[cnt].u = u;
e[cnt].v = v;
e[cnt].w = w;
e[cnt].nex = head[u];
head[u] = cnt ++;
}
ll bz[100007][20],ma[100007][20],mi[100007][20],depth[100007];
void dfs(ll u, ll fa) {
bz[u][0] = fa;
for (int i = head[u]; ~i; i = e[i].nex) {
ll to = e[i].v;
if (to == fa) continue;
depth[to] = depth[u] + 1L;///depth inc
ma[to][0] = e[i].w;
mi[to][0] = -999999999999999;
dfs(to, u);
}
}
ll lca(ll x, ll y) {
if (depth[x] < depth[y])
swap(x, y);
for (ll i = 18; i >= 0; i--) {
if (depth[bz[x][i]] >= depth[y])
x = bz[x][i];
}
if (x == y)
return x;
for (ll i = 18; i >= 0; --i) {
if (bz[x][i] != bz[y][i]) {
x = bz[x][i];
y = bz[y][i];
}
}
return bz[x][0];
}
int fa[maxn];
void fainit() {
for (int i = 1; i <= 2 * n; i++)
fa[i] = i;
}
ll find(ll x) {
if (x == fa[x])
return x;
else
return fa[x] = find(fa[x]);
}
node a[maxn];
bool cmp(node a, node b) {
return a.w < b.w;
}
bool vis[maxn];
void cal() {
for (ll i = 1; i <= 18; i++) {
for (ll j = 1; j <= n; j++) {
bz[j][i] = bz[bz[j][i - 1]][i - 1];
ma[j][i] = max(ma[j][i - 1], ma[bz[j][i - 1]][i - 1]);
mi[j][i] = max(mi[j][i - 1], mi[bz[j][i - 1]][i - 1]);
if (ma[j][i - 1] > ma[bz[j][i - 1]][i - 1])
mi[j][i] = max(mi[j][i], ma[bz[j][i - 1]][i - 1]);
else if (ma[j][i - 1] < ma[bz[j][i - 1]][i - 1])
mi[j][i] = max(mi[j][i], ma[j][i - 1]);
}
}
}
ll get(int u, int v, ll w) {
ll ret = -inf;
for (int i = 18; i >= 0; i--) {
if (depth[bz[u][i]] >= depth[v]) {
if (w != ma[u][i])
ret = max(ret, ma[u][i]);
else
ret = max(ret, mi[u][i]);
u = bz[u][i];
}
}
return ret;
}
int main() {
n = read,m = read;
init();
for(int i=1; i<=m; i++) {
a[i].u = read,a[i].v = read,a[i].w = read;
}
fainit();
sort(a+1,a+1+m,cmp);
ll tot = 0;
for(int i=1; i<=m; i++) {
int fau = find(a[i].u);
int fav = find(a[i].v);
if(fau == fav) continue;
tot += a[i].w;
fa[fau] = fav;
add(a[i].u,a[i].v,a[i].w);
add(a[i].v,a[i].u,a[i].w);
vis[i] = true;///used
}
// cout << tot <<endl;
mi[1][0] = -inf;
depth[1] = 0;
dfs(1,-1);
cal();
ll ret = inf;
for(int i=1; i<=m; i++) {
if(!vis[i]) {
int u = a[i].u;
int v = a[i].v;
ll w = a[i].w;
int _lca = lca(u,v);
ll maxx = get(u,_lca,w);
ll mini = get(v,_lca,w);
ret = min(ret,tot-max(maxx,mini)+w);
}
}
cout << ret <<endl;
return 0;
}
/**
**/
F. 异象石

难度适中
考虑增加一个点或减少一个点的时候,对答案产生了哪些贡献
#define PII pair<ll,ll>
map<PII, ll> mp;
ll n, m, _time = 0;
ll head[maxn];
struct node
{
ll u, v, w;
ll next;
} e[maxn << 1];
ll dep[maxn];/// save the depth of every node
ll fa[maxn][30], lg[maxn], cnt = 0;
ll ans;
ll dfn[maxn], id[maxn], vis[maxn], dis[maxn];
set<ll> s;
void init()
{
cnt = 0;
memset(head, -1, sizeof head);
}
void add(ll u, ll v, ll w)
{
e[cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(ll cur, ll rt)
{
dfn[cur] = ++_time;
id[_time] = cur;
fa[cur][0] = rt;
dep[cur] = dep[rt] + 1; /// the depth of the current node changed
dis[cur] = dis[rt] + mp[ {cur, rt}];
for(int i = 1; i <= lg[dep[cur]]; i++)
{
fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
}
for(int i = head[cur]; ~i; i = e[i].next) /// visit all linked nodes
{
if(e[i].v != rt) dfs(e[i].v, cur);
}
}
void cal()
{
for(int i = 1; i <= n; i++)
{
lg[i] = lg[i - 1] + (1LL << lg[i - 1] == i); /// 2 ^ lg[i-1] == i true + 1
}
}
ll lca(ll x, ll y)
{
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y) return x;
for(int k = lg[dep[x]] - 1; k >= 0; k --)
{
if(fa[x][k] != fa[y][k])
{
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
ll getDis(ll u, ll v)
{
ll _lca = lca(u, v);
return dis[u] + dis[v] - 2LL * dis[_lca];
}
void update(ll x)
{
ll y, z;
set<ll>::iterator it;
x = dfn[x];///time
if(!vis[id[x]]) s.insert(x);
it = s.lower_bound(x);
if(it == s.begin()) y = *--s.end();
else y = *--it;
y = id[y];
it = s.upper_bound(x);
if(it == s.end()) z = *s.begin();
else z = *it;
z = id[z];
if(vis[id[x]]) s.erase(x);
x = id[x];
int dis = getDis(x, y) + getDis(x, z) - getDis(y, z);
if(!vis[x]) vis[x] = 1, ans += dis;
else vis[x] = 0, ans -= dis;
}
signed main()
{
cin >> n;
cal();
init();
for(int i = 1; i < n; i++)
{
ll u = read, v = read, w = read;
mp[ {u, v}] = w;
mp[ {v, u}] = w;
add(u, v, w);
add(v, u, w);
}
dfs(1, 0);
m = read;
ll x;
char c;
for(int i = 1; i <= m; i++)
{
cin >> c;
if(c == '?') printf("%lld
", ans >> 1LL);
else
{
scanf("%lld", &x);
update(x);
}
}
// cout << ans << endl;
return 0;
}
/**
6
1 2 1
1 3 5
4 1 7
4 5 3
6 4 2
10
+ 3
+ 1
?
+ 6
?
+ 5
?
- 6
- 3
?
5
14
17
10
**/
G. 暗的连锁

难度适中
首先对n-1条边建图,然后对后来的m条边进行处理:
(从度的方面入手)
int u = read, v = read;
int _lca = lca(u, v);
deg[u] ++;
deg[v] ++;
deg[_lca] -= 2;
int n, m;
int root;
int head[maxn];
struct node
{
int u;
int v;
int w;
int next;
} e[maxn];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
int mini[maxn][30];
int lg[maxn];
int cnt = 0;
vector<int> son[maxn];
void init()
{
memset(head, -1, sizeof head);
}
void add(int u, int v)
{
e[cnt].u = u;
e[cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur, int rt)
{
fa[cur][0] = rt, dep[cur] = dep[rt] + 1; /// the depth of the current node changed
for(int i = 1; i <= lg[dep[cur]]; i++)
{
fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
}
for(int i = head[cur]; ~i; i = e[i].next) /// visit all linked nodes
{
if(e[i].v != rt) dfs(e[i].v, cur), son[cur].push_back(e[i].v);
}
}
void cal()
{
for(int i = 1; i <= n; i++)
{
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i); /// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x, int y)
{
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y])
{
x = fa[x][lg[dep[x] - dep[y]] - 1];
}
if(x == y) return x;
for(int k = lg[dep[x]] - 1; k >= 0; k --)
{
if(fa[x][k] != fa[y][k])
{
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int deg[maxn];
int ans;
void get(int u)
{
int siz = son[u].size();
for(int i = 0; i < siz; i++)
{
int to = son[u][i];
get(to);
deg[u] += deg[to];
}
if(!fa[u][0]) return ;
if(deg[u] == 1) ans ++;
else if(deg[u] == 0) ans += m;
}
int main()
{
cin >> n >> m;
cal();
init();
for(int i = 1; i < n; i++)
{
int u = read, v = read;
add(u, v);
add(v, u);
}
dfs(1, 0);
for(int i = 1; i <= m; i++)
{
int u = read, v = read;
int _lca = lca(u, v);
deg[u] ++;
deg[v] ++;
deg[_lca] -= 2;
}
get(1);
cout << ans << endl;
return 0;
}
/**
4 1
1 2
2 3
1 4
3 4
3
**/
H. 点的距离

板子题
考虑用深度代替距离即可
#define Clear(x,val) memset(x,val,sizeof x)
int n,m;
int root;
int head[maxn];
struct node {
int u;
int v;
int w;
int next;
} e[maxn << 1];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
ll dis[maxn];
int lg[maxn];
int cnt = 0;
void init() {
memset(head,-1,sizeof head);
}
void add(int u,int v) {
e[cnt].u = u;
e[cnt].v = v;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur,int rt) {
fa[cur][0] = rt,dep[cur] = dep[rt] + 1;/// the depth of the current node changed
for(int i=1; i <= lg[dep[cur]]; i++) {
fa[cur][i] = fa[fa[cur][i-1]][i-1];
}
for(int i=head[cur]; ~i; i = e[i].next) { /// visit all linked nodes
if(e[i].v != rt) dfs(e[i].v,cur);
}
}
void cal() {
for(int i=1; i<=n; i++) {
lg[i] = lg[i-1] + (1 << lg[i-1] == i);/// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x,int y) {
if(dep[x] < dep[y]) swap(x,y);
while(dep[x] > dep[y]) x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y) return y;
/// big -> small
for(int k = lg[dep[x]] - 1; k >= 0; k --) {
if(fa[x][k] != fa[y][k]) {
x = fa[x][k];
y = fa[y][k];
}
}
return fa[x][0];
}
int main() {
n = read;
cal();
init();
for(int i=1; i<n; i++) {
int u = read,v = read;
add(u,v);
add(v,u);
}
dfs(1,0);
m = read;
for(int i=1; i<=m; i++) {
int x = read,y = read;
int _lca = lca(x,y);
ll ans = dep[x] + dep[y] - 2 * dep[_lca];
printf("%lld
",ans);
}
return 0;
}
/**
6
1 2
1 3
2 4
2 5
3 6
2
2 6
5 6
**/
l. 晨跑

大水题
求三个数的lcm
int main()
{
ll a = read, b = read, c = read;
ll ans = lcm(lcm(a,b),c);
cout << ans <<endl;
return 0;
}
J. 货物运输

较简单
在维护某节点的2次方级祖先的同时,记录下路径的最小承重,即为答案
int n, m;
int root;
int head[maxn];
struct node
{
int u;
int v;
int w;
int next;
} e[maxn];
int dep[maxn];/// save the depth of every node
int fa[maxn][30];
int mini[maxn][30];
int lg[maxn];
int cnt = 0;
void init()
{
memset(head, -1, sizeof head);
}
void add(int u, int v, int w)
{
e[cnt].u = u;
e[cnt].v = v;
e[cnt].w = w;
e[cnt].next = head[u];
head[u] = cnt ++;
}
void dfs(int cur, int rt, int val)
{
fa[cur][0] = rt, dep[cur] = dep[rt] + 1; /// the depth of the current node changed
mini[cur][0] = val;
for(int i = 1; i <= lg[dep[cur]]; i++)
{
fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
mini[cur][i] = min(mini[cur][i - 1], mini[fa[cur][i - 1]][i - 1]);
}
for(int i = head[cur]; ~i; i = e[i].next) /// visit all linked nodes
{
if(e[i].v != rt) dfs(e[i].v, cur, e[i].w);
}
}
void cal()
{
for(int i = 1; i <= n; i++)
{
lg[i] = lg[i - 1] + (1 << lg[i - 1] == i); /// 2 ^ lg[i-1] == i true + 1
}
}
int lca(int x, int y)
{
int ans = 0x3f3f3f3f;
if(dep[x] < dep[y]) swap(x, y);
while(dep[x] > dep[y])
{
ans = min(ans, mini[x][lg[dep[x] - dep[y]] - 1]);
x = fa[x][lg[dep[x] - dep[y]] - 1];
}
if(x == y) return ans;
/// big -> small
for(int k = lg[dep[x]] - 1; k >= 0; k --)
{
if(fa[x][k] != fa[y][k])
{
ans = min(ans, mini[x][k]);
ans = min(ans, mini[y][k]);
x = fa[x][k];
y = fa[y][k];
}
}
ans = min(ans, mini[x][0]);
ans = min(ans, mini[y][0]);
// return fa[x][0];
return ans;
}
int main()
{
cin >> n >> m;
cal();
init();
for(int i = 1; i < n; i++)
{
int u = read, v = read, w = read;
add(u, v, w);
add(v, u, w);
}
dfs(1, 0, 0x3f3f3f3f);
for(int i = 1; i <= m; i++)
{
int u = read, v = read;
int ans = lca(u, v);
printf("%d
", ans);
}
return 0;
}
/**
6 5
1 2 2
2 3 5
2 4 2
2 5 3
5 6 1
2 4
6 2
1 3
3 5
1 6
**/
K. 数三角形
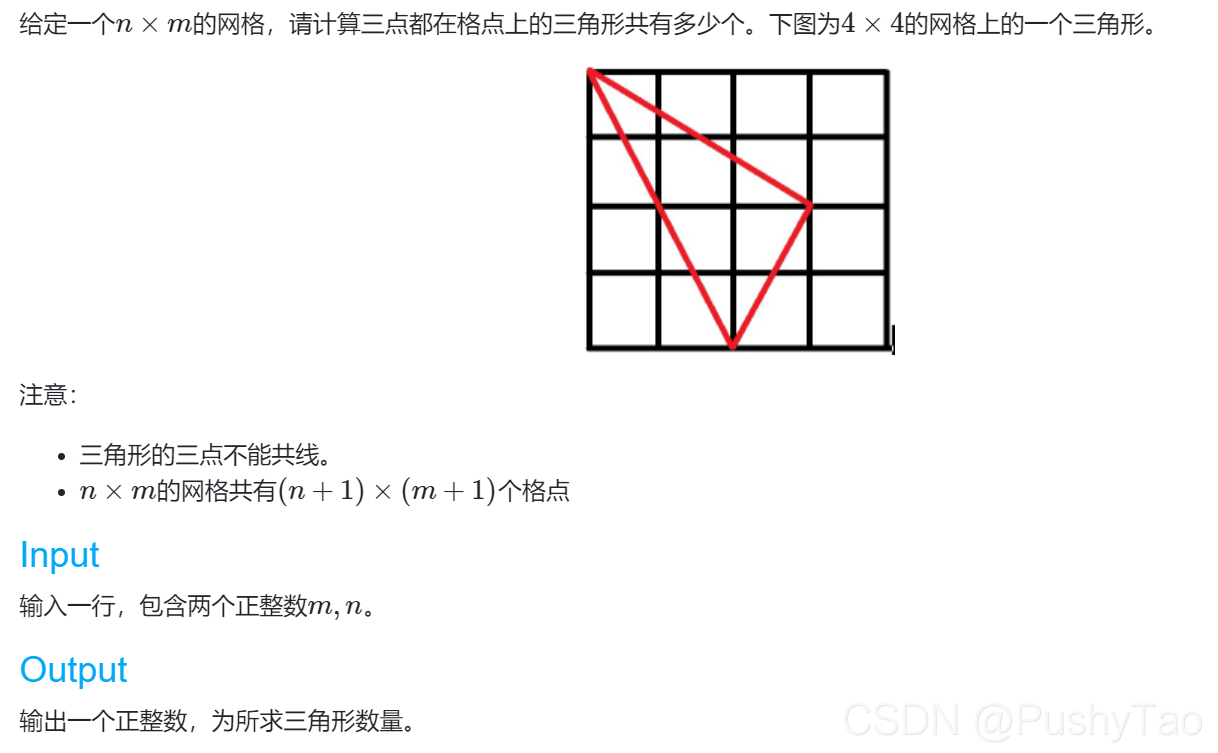
组合数学简单题
考虑容斥,减去不符合的情况
需要知道两个整数点之间的整数点的个数 博客第11条

ll cal(ll x){
ll ret = x * (x - 1) * (x - 2);
return ret / 6LL;
}
int n,m;
int main() {
n = read,m = read;
n ++,m ++;
ll tot = cal(n * m) - n* cal(m) - m * cal(n);
ll sub = 0;
// cout << tot <<endl;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
sub += (n - i) * (m - j) * (gcd(i,j) - 1);
}
}
cout << tot - sub * 2 <<endl;
return 0;
}/// ac_code
/**
**/