RSA的整体逻辑就是将一个数在经过一次运算后能变回原数,这个运算就是求幂然后取模,将这个运算拆成两个部分,其中一部分作为公钥给用户,另一部分作为私钥储存在服务器,用户用公钥运算后发送给服务器,然后服务器再用私钥运算,最终能得到还原后的数据,这就是RSA的算法流程
算法原理解释
所有涉及的知识(均只写出需要使用的部分)
互质关系
中国剩余定理
欧拉φ函数 费马-欧拉定理(数论)
模反元素
扩展欧几里得算法
蒙哥马利算法
互质关系
涉及的结论 1. 任意两个质数构成互质关系,比如13和61 2. 一个数是质数,另一个数只要不是前者的倍数,两者就构成互质关系,比如3和10 3. 如果两个数之中,较大的那个数是质数,则两者构成互质关系,比如97和57 4. 1和任意一个自然数是都是互质关系,比如1和99 5. p是大于1的整数,则p和p-1构成互质关系,比如57和56
中国剩余定理
取两个质数n、m,则对于任意正整数x < n * m,均有唯一的(a,b)数对使得a = x mod n、b = x mod m
例:
取n = 3,m = 5,则n * m = 15
x a b
14 2 4
13 1 3
12 0 2
11 2 1
10 1 0
9 0 4
8 2 3
7 1 2
6 0 1
5 2 0
4 1 4
3 0 3
2 2 2
1 1 1
其中a有n - 1个不为0的值,b有m - 1个不为0的值,x有(n - 1)(m - 1)个不为0的值
欧拉φ函数
对正整数n,欧拉函数φ(n)是小于或等于n的正整数中与n互质的数的数目
因为需要将比n小且不互质的整数去除掉,则根据容斥定理,可以得到
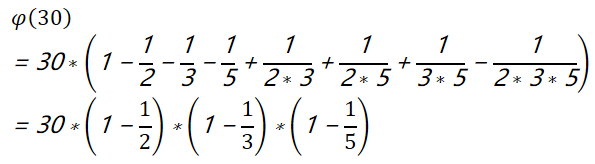
即φ函数公式为:
当n=p*q,其中p和q均为质数时,乘积性质证明:
方法一:
![]() ①
①
证毕
方法二:
根据中国剩余定理,x与(a,b)数对一一对应,则:
当a、b均不为0时,(a,b)所对应的x与n * m互质,因为n、m均为质数,则φ(n)= n - 1,φ(m)= m - 1
根据排列组合,(a,b)数对的数量为φ(n)*φ(m),也等于φ(n * m)的数量,即φ(n * m)=φ(n)* φ(m)
证毕
例:
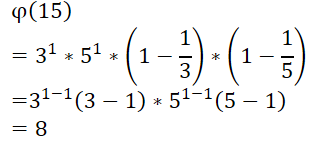
与中国剩余定理中的红色行数一致,并且通过剩余定理,可以有另一种思路推出φ函数公式,参考文末链接
欧拉定理
若a与n互质,则
证明:
设大整数m的欧拉函数为φ(m),表示比m小的正整数中与m互质的数的个数,将此类数记为
同时设
![]()
定理一
p之间两两模m不同余
证明
若存在两个数pi和pj模m同余,则
![]()
将p = ax代入,得
![]()
因为a与m互质,则xi-xj必然是m的倍数,然而xi-xj小于m,且不等于0,矛盾
因此,pi和pj模m不同余,证毕
定理二
任意p模m的结果都与m互质
证明
根据扩展欧几里得算法,得
![]()
证毕
因为任意p模m的结果都与m互质,且p直接两两模m不同余,则p与x存在双射关系,即一一对应
于是将所有p的乘积模m可得

因为任意x都与n互质,则
![]()
证毕
模反元素
如果两个正整数a和n互质,那么一定可以找到整数b,使得 ab-1 被n整除,或者说ab被n除的余数是1,即
证明:
因为a与n互质,则由②得
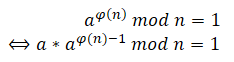
即一定存在b,使得a与b为模反元素
扩展欧几里得算法
在③中,RSA算法一般将质数a取为65537,二进制表示为10000000000000001,因为绝大部分位置是0,因此简化了加密时的运算量
在1024位加密下,质数p和q随机取为512位二进制数,使得n为1024位,然后根据a和n,求得a的模反元素b
但是在实际计算过程中,如此大的幂运算,是几乎不可能直接计算出来的,因此使用了扩展欧几里得算法来计算
欧几里得算法就是熟知的辗转相除法
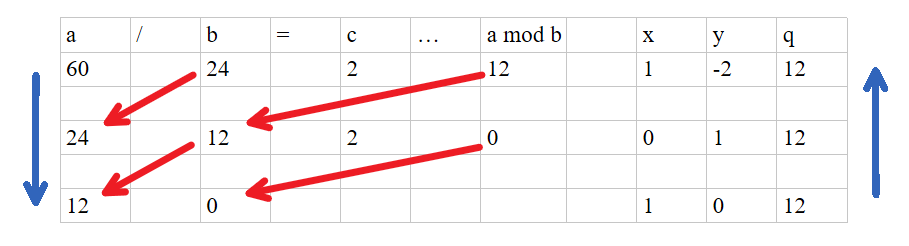
从上图中可看出,通过辗转相除,最后在b等于0时能得到最大公约数gcd,此处记为q,在扩展欧几里得算法中,使用了递归的计算,可以在得到gcd的同时得到使等式ax+by=gcd(a,b)成立的x和y,因此数据出现的顺序是如蓝色箭头所示
直接看最后一行的数据,当b=0时计算结束,a*1+b*0=q,即ax+by=q,得到gcd,此时的a和b为上一层的b和a mod b
将最后一行的等式带入倒数第二行,可得bx+(a mod b)y=q,如果使用取整来表示模运算,并整理等式,可得
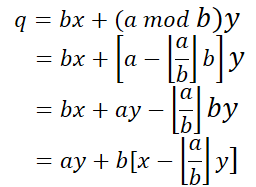
对于第二行,根据ax+by=q的公式,x与y将因此更新为
![]()
通过整个递归算法,最终可以得到使第一行即原式成立的x和y,以及gcd,如果递归层数较多,也可以改用迭代计算
蒙哥马利算法
对于任意的整数a、b、q、r、n,我们可以构造
则可得
![]()
即
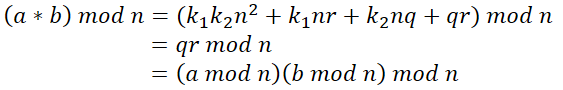
则得到模运算的乘法分配律
利用乘法分配律可以轻松得到某些幂的模
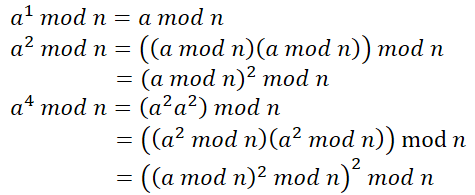
观察规律,则可以直接写出所有幂为2^n的数对n的模,下面展示两个,后面的以此类推
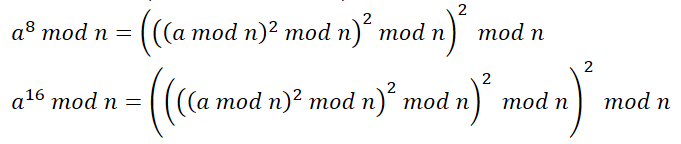
而其他的幂则可以通过上述结果累加得到,假设幂为19,则
![]()
将19拆分后利用乘法分配律可以得到以下结果

将拆分后的数从大到小逐个提出,然后利用分配律拆开,整理后可以得到最后一行的形式,每增加一个数x,则乘以(a^x mod n),然后将乘积mod n,而所有(a^x mod n)都可以用上述规律得到,从小到大计算则可以一次得到结果
RSA算法
下面展示1024位加密算法的步骤
第一步:
随机取两个512位二进制长度的质数p和q,表示成十进制,以便后续运算,其中取随机数可以参考Rabin-Miller方法
第二步:
计算p和q的乘积n,然后由①可得φ(n)=(p-1)(q-1)
第三步:
根据③,将a、b分别记为e、d,意为encode和decode,其中e常设为65537,也可使用其他质数,然后根据扩展欧几里得算法求得d
第四步:
将e和n封装为公钥,d和n封装为私钥,将公钥发送给用户,然后将私钥保存在服务器端
第五步:
加解密的算法都是相同的,为大数幂的模运算,使用蒙哥马利算法计算,文本内容需要全部转换为十进制,可以存为ascii码或者unicode码,
同时,要保证每一段的字符串长度小于n的长度,以1024位加密为例,n的十进制长度为154,以ascii码为例,左侧补零保证所有字符为3位,
则最多可以放下51个字符,然后分段加密和解密,加密时以分段后的原文为底,e为幂,对n取模,解密时以分段后的密文为底,d为幂,对n取模
使用方法:
用户使用公钥加密后传输给服务器,服务器使用储存的私钥解密即完成整个RSA加密流程
可行性证明
假设已经得到e、d、n,设m为原文,c为密文,则可通过第一行得到c,然后需要证明第二行,即c能通过变化回到m
证明:
将c带入二式,得
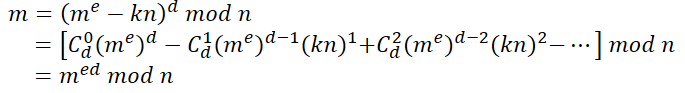 ⑤
⑤
由③可得
![]()
即
![]()
将上式带入⑤,得
![]()
如果m与n互质,则
![]()
证毕
如果m与n不互质,因为n是p和q的乘积,则m必然等于kp或者kq,以m = kp为例,因为k < q且q是质数,所以k与q互质,则
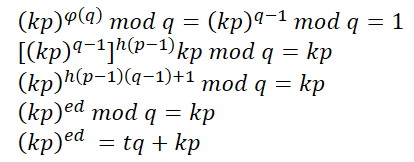
变形上式可得
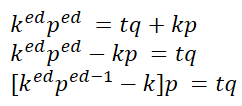
因为左边是p的倍数,右边必然是p的倍数,因为p和q互质,所以t必然是p的倍数,记t=t'p,带回原式,得
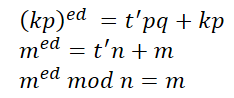
证毕
算法实践
在链接中有python实现的rsa算法,也有使用该算法的IoT软硬件,可以自行尝试,如果遇到任何问题,欢迎建议与留言!
https://github.com/Pyrokine/usb_power_meter/blob/master/FIRMWARE/python/myRSA.py
感谢
算法导论 null RSA算法原理(一) http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
ACM数论之旅7---欧拉函数的证明及代码实现(我会证明都是骗人的╮( ̄▽ ̄)╭)
https://www.cnblogs.com/linyujun/p/5194170.html
25行代码实现完整的rsa算法(python3.x版本)
https://blog.csdn.net/bian_h_f612701198412/article/details/87202462
扩展欧几里得算法详解
https://blog.csdn.net/destiny1507/article/details/81750874
模运算的分配律如何证明?
https://www.zhihu.com/question/41361614
费马小定理、欧拉定理与扩展欧拉定理(含证明)
https://blog.csdn.net/hzj1054689699/article/details/80693756
浅谈欧拉定理的证明
https://www.cnblogs.com/wangxiaodai/p/9758242.html