title: 算法
tags: 算法
算法(Algorithm):一个计算过程,解决问题的方法
递归
递归的两个特点:
- 调用自身
- 结束条件
def func3(x):
if x > 0:
print(x)
func3(x - 1)
func3(3)
def func3(x):
if x > 0:
func3(x - 1)
print(x)
func3(3)
![]
(http://images2017.cnblogs.com/blog/658994/201708/658994-20170825224958418-638409811.jpg)
![]
(http://images2017.cnblogs.com/blog/658994/201708/658994-20170825225002980-1149857509.jpg)
我的小鲤鱼
![]
(http://images2017.cnblogs.com/blog/658994/201708/658994-20170825225900949-574999163.png)
def func(depth):
if depth == 0:
print('我的小鲤鱼',end='') # end = '' 代表不换行
else:
print('抱着',end='')
func(depth-1)
print('的我',end='')
func(3)
时间复杂度
评估算法运行效率的
时间复杂度是算法运行时间的式子
时间复杂度可以用表示时间复杂度的数和单位共同组成 ,单位就是n的几次方
O(1)
O(n)
O(n^2)
O(n^3)
![]
(http://images2017.cnblogs.com/blog/658994/201708/658994-20170825230649480-1075677653.jpg)
while循环 折半
O(log2n)
总结
时间复杂度是用来估计算法运行时间的一个式子(单位)。
一般来说,时间复杂度高的算法比复杂度低的算法慢。不同量级的不能比较
- 常见的时间复杂度(按效率排序)
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n2logn)<O(n^3) - 不常见的时间复杂度(看看就好)
O(n!) O(2n) O(nn) …
如何一眼判断时间复杂度?
循环减半的过程 O(logn)
几次循环就是n的几次方的复杂度
时间复杂度按照最大的来判断
空间复杂度
内存占用大小
O(1)
Sn = O(n)
空间换时间 算法跑的快
列表查找
从列表中查指定元素
输出:元素下标或未找到元素
顺序查找
从头开始查找,直到查找到结果
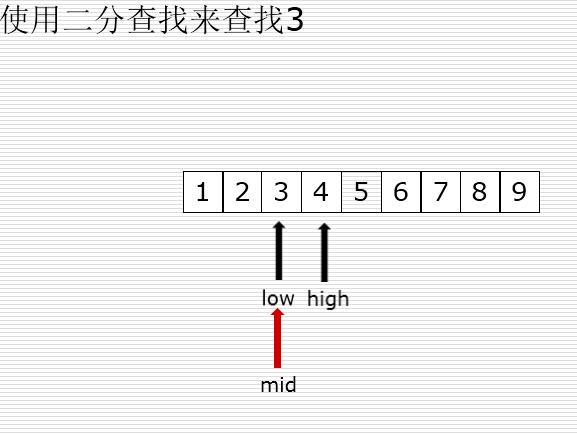
二分查找
有序的列表查找
val < mid : high = mid -1
val > mid : low = mid +1
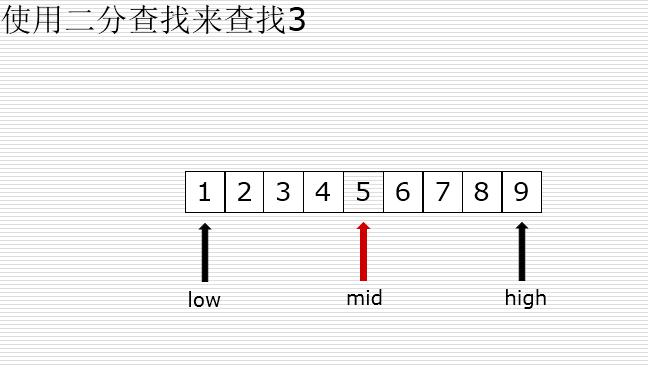
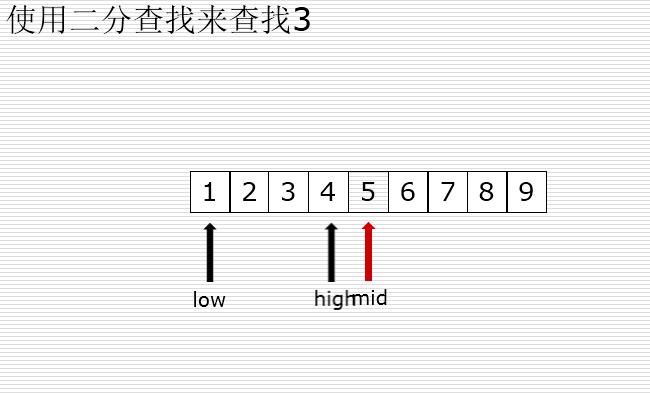
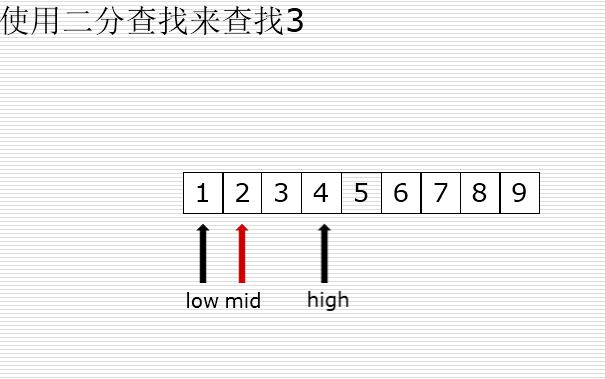
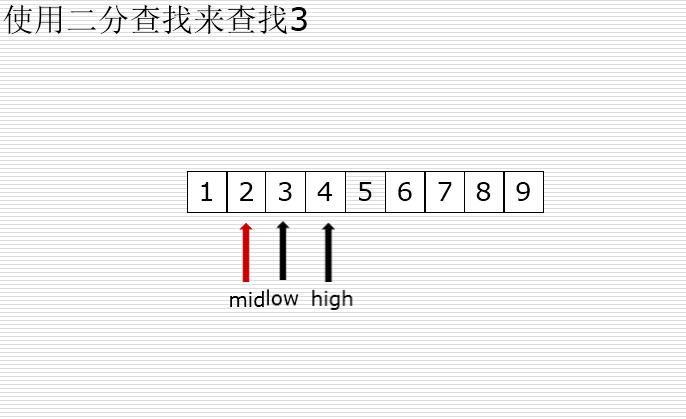
二分法和顺序查找测试
In [1]: import random
...: n = 10000
...: li = list(range(n))
...:
...: def bin_searhc(li, val):
...: low = 0
...: high = len(li) - 1
...: while low <= high:
...: mid = (low + high) // 2
...: if li[mid] == val:
...: return mid
...: elif li[mid] < val:
...: low = mid + 1
...: else:
...: high = mid - 1
...: return None # 单high < low 的时候不存在
...:
In [2]:
In [2]: %timeit bin_searhc(li,3200)
The slowest run took 4.12 times longer than the fastest. This could
intermediate result is being cached.
100000 loops, best of 3: 5.08 µs per loop
In [3]: %timeit li.index(3200)
10000 loops, best of 3: 64.3 µs per loop
- index 的时间复杂度是O(n)
- bin_search的时间复杂度是O(logn)
2**64 仅仅查找64次
O(logn)
所以最后相差的会很大
尾递归的和二分速度差不多
尾递归没有在出栈的时候的保存,所以速度快
出栈的时候不会保存变量
def bin_search_rec(data_set, value, low, high):
if low <= high:
mid = (low + high) // 2
if data_set[mid] == value:
return mid
elif data_set[mid] > value:
return bin_search_rec(data_set, value, low, mid - 1)
else:
return bin_search_rec(data_set, value, mid + 1, high)
else:
return
li =[
{'id': 1001, 'name': "张三", 'age': 20},
{'id': 1002, 'name': "李四", 'age': 25},
{'id': 1004, 'name': "王五", 'age': 23},
{'id': 1007, 'name': "赵六", 'age': 33}
]
def bin_searhc(li, val):
low = 0
high = len(li) - 1
while low <= high:
mid = (low + high) // 2
if li[mid]['id'] == val:
return li[mid]
elif li[mid]['id'] < val:
low = mid + 1
else:
high = mid - 1
return None # 单high < low 的时候不存在
res = bin_searhc(li,1002)
print(res)
列表排序
sort()
LowB 三人组
关键点:
趟
有序区
无序区
冒泡排序
"""
冒泡排序,注意的关键点是有序区和无序区
比较相邻的两个数的大小,如果前面的数比后面的数大,则交换,
交换完一次称为一趟,每一趟的指针:n-i-1(ns是总数,i是趟数),即每一趟遍历的个数
"""
import time
import random as rd
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
x = func(*args, **kwargs)
t2 = time.time()
print("%s running time is %s sec" % (func.__name__, t2 - t1))
return x
return wrapper
@cal_time
def bubble_sort(li):
"""
第一层的for循环是趟
第二层的for循环是每一趟中比较相邻两个数的大小
:param li:
:return:
"""
for i in range(len(li) - 1):
for j in range(len(li) - i - 1):
if li[j] > li[j + 1]:
li[j], li[j + 1] = li[j + 1], li[j]
return li
@cal_time
def sys_sort(li):
li.sort()
return li
"""
冒泡排序的时间测试
"""
# li = [ i for i in range(1000)]
li = list(range(5000))
rd.shuffle(li) # 用shuffle对li洗牌 是直接操作的li
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(bubble_sort(li))
bubble_sort(li1)
sys_sort(li2)
冒泡排序的时间复杂度是O(n^2)
通过和系统的sort运行比较,内置的sort高两个数量级:
bubble_sort running time is 3.966226577758789 sec
sys_sort running time is 0.0020003318786621094 sec
冒泡排序的改进
最坏情况和一般情况下,冒泡排序的时间复杂度是O(n^2),最好情况是O(n)
def bubble_sort(li):
"""
第一层的for循环是趟
第二层的for循环是每一趟中比较相邻两个数的大小
最好情况:相邻的数已经排列好了,没有交换,通过设置标志位
:param li:
:return:
"""
for i in range(len(li) - 1):
exchange = False
for j in range(len(li) - i - 1):
if li[j] > li[j + 1]:
li[j], li[j + 1] = li[j + 1], li[j]
exchange = True
if not exchange:
break
return li
选择排序
在一个列表中中删除一个元素的时候 时间复杂度是O(n),
后面的补过来 len()-1
把最小的数放到有序区
把第一个数定义成最小的
第一趟找到最小的数
"""
选择排序:一趟遍历中找最小的数,放到有序区的第一个位置,后面依次找最小的数,并依次排列
"""
import time
import random as rd
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
x = func(*args, **kwargs)
t2 = time.time()
print("%s running time is %s sec" % (func.__name__, t2 - t1))
return x
return wrapper
@cal_time
def select_sort(li):
for i in range(len(li) - 1): # i 是趟
min_lock = i # i是索引
# 找i位置到最后最小的数
for j in range(i, len(li)): # i可以是i+1 省去和自己比 也代表了无序区的第一个数
if li[j] < li[min_lock]:
min_lock = j
# 和无序区第一个数交换 此时的i是无序区的第一个数的索引
li[min_lock], li[i] = li[i], li[min_lock]
return li
@cal_time
def sys_sort(li):
li.sort()
return li
"""
冒泡排序的时间测试
"""
# li = [ i for i in range(1000)]
li = list(range(1000))
rd.shuffle(li) # 用shuffle对li洗牌 是直接操作的li
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(select_sort(li1))
select_sort(li1)
sys_sort(li2)
插入排序
关键点:
摸到的牌
手里的牌
"""
插入排序:列表被分成有序区和无序区两部分,最初有序区只有一个元素,无序区从1~n-1,从无序区中找摸牌,插入到有序区中
插入排序的有序区是变化的,
把摸到的牌存到临时变量,然后和手里的最后一张牌比较,指针开始在最后一张牌,(指针是j)
"""
import time
import random as rd
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
x = func(*args, **kwargs)
t2 = time.time()
print("%s running time is %s sec" % (func.__name__, t2 - t1))
return x
return wrapper
@cal_time
def insert_sort(li):
for i in range(1, len(li)): # i代表的是手里的牌,默认第一张是放在有序区,从无序区中摸牌
tmp = li[i] # 从后面开始摸牌,存到临时变量
j = i - 1 # j代表的是手里的最后一张牌的下标
while True:
if j < 0 or tmp >= li[j]:
break
li[j + 1] = li[j] # 手里的最后一张牌向后移
j -= 1 # 指针向后移动一位
li[j + 1] = tmp # 把临时变量放在j+1的位置
return li
@cal_time
def sys_sort(li):
li.sort()
return li
"""
排序的时间测试
"""
# li = [ i for i in range(1000)]
li = list(range(1000))
rd.shuffle(li) # 用shuffle对li洗牌 是直接操作的li
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(insert_sort(li1))
insert_sort(li1)
sys_sort(li2)
快速排序
归位,左右进行递归 还有0个 一个元素的时候停止递归
返回的是下标
递归至少有2个条件 left<right
position函数最重要
临时变量data[left]
对称
防止超过递归深度
设置递归层数
快排的时间复杂度:
partition O(n)
"""
快速排序:关键是归位和递归,归位后返回的是归位的下标mid,mid把列表分成左右两部分,
递归的条件:left<right,至少有两个元素,只有一个元素的时候,结束递归
左侧范围:left~mid-1
右侧范围:mid+1~right
"""
import time
import random as rd
import copy
sys.setrecursionlimit(99999) # setrecursionlimit 设置递归最大深度限制
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
x = func(*args, **kwargs)
t2 = time.time()
print("%s running time is %s sec" % (func.__name__, t2 - t1))
return x
return wrapper
def _quick_sort(data, left, right):
if left < right:
mid = partition(data, left, right)
_quick_sort(data, left, mid - 1) # 左边的范围
_quick_sort(data, mid + 1, right) # 右边的范围
# 归位函数
def partition(data, left, right):
tmp = data[left]
while left < right:
while left < right and data[right] >= tmp:
right -= 1
data[left] = data[right] # 把右面比tmp小的放左边
while left < right and data[left] <= tmp:
left += 1
data[right] = data[left] # 把左边比tmp大的放到右边
data[left] = tmp # 此时left = right
return left # 返回tmp的坐标
@cal_time
def quick_sort(data):
# 快排中有递归 装饰器会多次执行
return _quick_sort(data, 0, len(data) - 1)
@cal_time
def sys_sort(li):
li.sort()
return li
"""
排序的时间测试
"""
# li = [ i for i in range(1000)]
li = list(range(1000))
rd.shuffle(li) # 用shuffle对li洗牌 是直接操作的li
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(quick_sort(li1))
sys_sort(li2)
quick_sort(li1)
快排的问题:
- O(nlogn) 每一层是logn 一共有n层
- 倒序的列表并没有分成两部分,每一次只排一个 O(n^2)
- 最坏情况的复杂度是O(n^2)
解决方式:随机化的快排
随机选一个数,放到最左侧(算法导论是右侧)
递归过多的时候会导致栈溢出
降序排列
堆排序
树与二叉树
树是一种数据结构
二叉树的存储方式
最后的非叶子节点
len(data)//2 -1
向下调整
二叉树从根----叶子 logn
python内置heapq 堆模块
归并排序
把一个列表分成两部分,一次归并
挨着换的稳定 飞换的是不稳定的
希尔排序
分组 + 插入
"""
希尔排序:先分组 后插入排序
"""
import time
import random as rd
import copy
def cal_time(func):
def wrapper(*args, **kwargs):
t1 = time.time()
x = func(*args, **kwargs)
t2 = time.time()
print("%s running time is %s sec" % (func.__name__, t2 - t1))
return x
return wrapper
def insert_sort_gap(li, gap):
for i in range(gap, len(li)):
tmp = li[i]
j = i - gap
while j >= 0 and tmp < li[j]:
li[j + gap] = li[j]
j = j - gap
li[j + gap] = tmp
@cal_time
def shell_sort(li):
d = len(li) // 2
while d > 0:
insert_sort_gap(li, d)
d = d // 2
return li
@cal_time
def sys_sort(li):
li.sort()
return li
"""
排序的时间测试
"""
# li = [ i for i in range(1000)]
li = list(range(10000))
rd.shuffle(li) # 用shuffle对li洗牌 是直接操作的li
li1 = copy.deepcopy(li)
li2 = copy.deepcopy(li)
# print(shell_sort(li1))
sys_sort(li2)
shell_sort(li1)
计数排序
内存占用大,用空间换时间