2.4 逆矩阵

文章目录

• 方阵的行列式
• • 性质
  • • 例题
• 伴随矩阵(只有方阵才有伴随矩阵)
• • 定理
• 逆矩阵的定义
• 1)如何判断一个矩阵可逆？2)$A^{-1}=?$
• • 定理
  • 求逆矩阵的方法
  • • 例题
• 逆矩阵的性质
• 伴随矩阵$A^{\ast }$小结
• 参考

---

线性代数请记住：永远不要把矩阵放在分母上

方阵的行列式

对一个方阵求行列式，就是把一个数表变成了一个数，行列式是矩阵的一个属性，矩阵有很多属性如：特征值、特征向量、行列式…

性质

例题

---

伴随矩阵(只有方阵才有伴随矩阵)

求一个n阶方阵$A$的伴随矩阵的步骤为：

• 1、求所有元素的代数余子式
• 2、按行求的代数余子式按列放，构成一个矩阵就是伴随矩阵记为$A^{\ast }$
  口诀：按行求，按列放
  

定理

对任意方阵A有：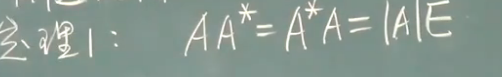

推论:对任意方阵A有：$|A^{\ast }|=|A{|}^{n-1}$

---

逆矩阵的定义

逆矩阵满足下面的基本事实：

3)$A{A}^{-1}=A^{-1}A=E$

---

1)如何判断一个矩阵可逆？2)$A^{-1}=?$

这里有个概念，如果矩阵A的行列式不为0，则称这个矩阵非奇异、非退化、满秩、可逆

定理

这个定理的证明是通过逆矩阵的定义证明的

下面这个推论只需证明AB=E则A可逆，而定义需要证明AB=E且BA=E

---

求逆矩阵的方法

1、上面提到的伴随矩阵法（计算量大）
2、初等变换法

例题

一个矩阵一定要判断可逆才能写逆矩阵

解矩阵方程需要注意的点：

---

逆矩阵的性质

---

伴随矩阵$A^{\ast }$小结

---

参考

以上图片均摘自宋浩老师视频，以方便以后自己查阅，感谢宋老师。
视频传送门