[TOC]
相关知识点
LP线性规划问题
- Linear Problem
- [百度百科]：研究线性约束条件下线性目标函数的极值问题的数学理论和方法。
学过运筹学的小伙伴，可以看这个LP问题的标准型来回顾一下：
不太熟悉的朋友可以看这个例题，再结合上面的标准型，来感受一下：
MIP混合整数规划
- Mixed Integar Planing
- 混合整数规划是LP的一种，决策变量部分是整数，不要求全部都是整数的规划问题。
- 这里MIP的求解器是使用CBC（Corn-or Branch and Cut）
- CBC (COIN-OR Branch and Cut) is an open-source mixed integer programming solver working with the COIN-OR LP solver CLP and the COIN-OR Cut generator library Cgl. The code has been written primarily by John J. Forrest. 更多详情看这里，但是笔者认为没啥必要。
MIP的Python实现（Ortool库）
我们来看一道简单的例题：
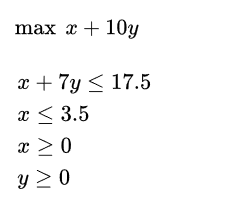其中x,y都是整数
from ortools.linear_solver import pywraplp
# 首先，调用CBC求解器
# 整数规划使用pywraplp.Solver.GLOP_LINEAR_PROGRAMMING
solver = pywraplp.Solver('SolveIntegerProblem',
pywraplp.Solver.CBC_MIXED_INTEGER_PROGRAMMING)
# 定义x和y的定义域，这里是从0到正无穷
x = solver.IntVar(0.0, solver.infinity(), 'x')
y = solver.IntVar(0.0, solver.infinity(), 'y')
# 添加约束：x+7y<17.5
constraint1 = solver.Constraint(-solver.infinity(), 17.5)
constraint1.SetCoefficient(x, 1)
constraint1.SetCoefficient(y, 7)
# 添加约束：x <= 3.5
constraint2 = solver.Constraint(-solver.infinity(), 3.5)
constraint2.SetCoefficient(x, 1)
constraint2.SetCoefficient(y, 0)
# 定义目标函数： Maximize x + 10 * y
bjective = solver.Objective()
objective.SetCoefficient(x, 1)
objective.SetCoefficient(y, 10)
objective.SetMaximization()
# 获取问题的答案
result_status = solver.Solve()
# 判断结果是否是最优解
assert result_status == pywraplp.Solver.OPTIMAL
# 验证一下结果是否正确，这一步不是必要但是推荐加上
assert solver.VerifySolution(1e-7, True)
# 输出结果
print('Number of variables =', solver.NumVariables())
print('Number of constraints =', solver.NumConstraints())
print('Optimal objective value = %d' % solver.Objective().Value())
variable_list = [x, y]
for variable in variable_list:
print('%s = %d' % (variable.name(), variable.solution_value()))
可以看一下自己运行的结果：
assert
这里涉及python 的一个assert的语法，不懂得可以简单看一下： Python assert（断言）用于判断一个表达式，在表达式条件为 false 的时候触发异常。 断言可以在条件不满足程序运行的情况下直接返回错误，而不必等待程序运行后出现崩溃的情况，
