基本概念
图
定义: 图G(V,E)是指一个二元组(V(G),E(G)),其中:
- V(G)={v1,v2,…, vn}是非空有限集,称为顶点集,
2. E(G)是V(G)中的元素对(vi,vj)组成的集合称为边集。
举例:

V(G)={v1,v2,v3,v4}
E(G)= {e1,e2,e3,e4,e5,e6}
- 若图G的边是有方向的,称G是有向图,有向图的边称为有向边或弧。
- 与同一条边关联的两个端点称为相邻的顶点
- 与同一个顶点关联的两条边称为相邻的边
- 端点重合为一点的边称为环
- 若一对顶点之间有两条以上的边联结,则这些边称为重边.
- 既没有环也没有重边的图,称为简单图.
- 若图G的每一条边e 都赋以一个实数w(e),称w(e)为边e的权, G连同边上的权称为赋权图 ,
- 图G的中顶点的个数, 称为图G的阶
- 图中与某个顶点相关联的边的数目,称为该顶点的度。
- 完全图:若无向图的任意两个顶点之间都存在着一条边,称此图为完全图。
邻接矩阵
- 以下均假设图为简单图,没有重边和环
- 图G的邻接矩阵是表示顶点之间相邻关系的矩阵

举个例子:


最大流问题
-
设G(V,E)为有向图,若在每条边e上定义一个非负权c, 则称图G为一个网络,称c为边e的容量函数,记为c(e)。
-
若在有向图G(V,E)中有两个不同的顶点vs与vt ,
若顶点vs只有出度没有入度,称vs为图G的源, -
若顶点vt只有入度没有出度, 称vt为G的汇,
-
若顶点v 既不是源也不是汇, 称为v中间顶点。
 如图,就是从v1到v9怎么流动,在受每一个有向边的流动最大限制下,才是最大流。大学考试的内容一般都是用手算的,这里我们还是用python来解决最大流问题。
如图,就是从v1到v9怎么流动,在受每一个有向边的流动最大限制下,才是最大流。大学考试的内容一般都是用手算的,这里我们还是用python来解决最大流问题。
python解决最大流问题

from ortools.graph import pywrapgraph
start_nodes = [0, 0, 0, 1, 1, 2, 2, 3, 3]
end_nodes = [1, 2, 3, 2, 4, 3, 4, 2, 4]
capacities = [20, 30, 10, 40, 30, 10, 20, 5, 20]
max_flow = pywrapgraph.SimpleMaxFlow()
for i in range(0, len(start_nodes)):
max_flow.AddArcWithCapacity(start_nodes[i], end_nodes[i], capacities[i])
# Find the maximum flow between node 0 and node 4.
if max_flow.Solve(0, 4) == max_flow.OPTIMAL:
print('Max flow:', max_flow.OptimalFlow())
print('')
print(' Arc Flow / Capacity')
for i in range(max_flow.NumArcs()):
print('%1s -> %1s %3s / %3s' % (
max_flow.Tail(i),
max_flow.Head(i),
max_flow.Flow(i),
max_flow.Capacity(i)))
print('Source side min-cut:', max_flow.GetSourceSideMinCut())
print('Sink side min-cut:', max_flow.GetSinkSideMinCut())
else:
print('There was an issue with the max flow input.')
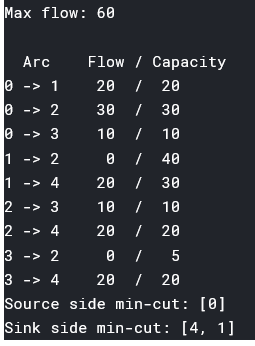
运行结果如下:
python解决最大流最小费用问题
跟最大流问题类似,但是每一条边多了一个费用的概念

- 从图中可以看到,0点生产了20个货物,然后要送5个到3,15个到4
- 一条边(15,4)意味着这个最多可以运输15个货物,每运输一个货物就要支付4点费用
from ortools.graph import pywrapgraph
#between each pair. For instance, the arc from node 0 to node 1 has acapacity of 15 and a unit cost of 4.
start_nodes = [ 0, 0, 1, 1, 1, 2, 2, 3, 4]
end_nodes = [ 1, 2, 2, 3, 4, 3, 4, 4, 2]
capacities = [15, 8, 20, 4, 10, 15, 4, 20, 5]
unit_costs = [ 4, 4, 2, 2, 6, 1, 3, 2, 3]
# Define an array of supplies at each node.
supplies = [20, 0, 0, -5, -15]
# Instantiate a SimpleMinCostFlow solver.
min_cost_flow = pywrapgraph.SimpleMinCostFlow()
# Add each arc.
for i in range(0, len(start_nodes)):
min_cost_flow.AddArcWithCapacityAndUnitCost(start_nodes[i], end_nodes[i],
capacities[i], unit_costs[i])
# Add node supplies.
for i in range(0, len(supplies)):
min_cost_flow.SetNodeSupply(i, supplies[i])
# Find the minimum cost flow between node 0 and node 4.
if min_cost_flow.Solve() == min_cost_flow.OPTIMAL:
print('Minimum cost:', min_cost_flow.OptimalCost())
print('')
print(' Arc Flow / Capacity Cost')
for i in range(min_cost_flow.NumArcs()):
cost = min_cost_flow.Flow(i) * min_cost_flow.UnitCost(i)
print('%1s -> %1s %3s / %3s %3s' % (
min_cost_flow.Tail(i),
min_cost_flow.Head(i),
min_cost_flow.Flow(i),
min_cost_flow.Capacity(i),
cost))
else:
print('There was an issue with the min cost flow input.')
运行结果:

参考:
ortool 官网