写在前面的
经过一天的努力终于将数字图像处理的第一次实验课完成了,有点小激动,写一篇课程报告,在写之前特意咨询了胡老师,课程报告有没有固定格式?得到的回答是否定的,不需要固定格式,心中不免有些欢喜,所以索性这篇课程报告成了我的第一篇DIP学习笔记。并且我会在后面附上我的源程序。
作业要求:
读图(Chapter2_1.pgm)、顺时针方向旋转15º(利用上述几种插值方法)、输出图像(测试图像见下图),可用C++或Matlab编程。
要评估量化插值效果,并对结果进行讨论;
提示:可正反转回到原点,然后比较未转的图像;
如何定义评估量、其计算的合理性、原点的精确匹配等都要仔细考虑证实;

Chapter2_1.pgm
注意到了没有,这次作业的难点不在图像的旋转,而在于你如何评价图像旋转的好坏。
硬件平台:
因为上次采集数据集的需求,我的电脑在研究室算是比较好的了,请允许我再窃喜一次,嘿嘿。我使用的是一台惠普Z440工作站,CPU是英特尔至强系列E5-1650,主频3.5GHz,内存16GB,硬盘256固态加2T机械磁盘阵列。
软件平台:
我使用win10系统、其中图像的旋转是在VS2015上使用openCV库,C++编程实现的,最后的性能评价是在matlab2016a上进行分析的。
实验过程:
先说一下试验的总体过程,整个实验分为两部分,一部分使用openCV库函数实现,主要实现图片的2次旋转操作,两次旋转都需要对图片的分辨率也就是大小进行操作,因为你要保证旋转是保留图像边沿,又要在旋转回原位时保证和原图一样的大小,然后将原图和最终旋转后的图像存储为txt格式,方便后续的matlab读取和操作。另一部分是用matlab编程实现对5种插值方法的比较,我主要使用了PSNR即“Peak Signal to Noise Ratio”的缩写,即峰值信噪比进行比较两幅图像的相似度,还有图像矩阵的均方差,以及相关系数,这三种评价标准对5种插值方法进行比较。
实验细节:
首先说一下第一部分,这部分比较困难,普及一下仿射变换,什么是仿射变换呢?引号中引自百度百科“仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。仿射变换是在几何上定义为两个向量空间之间的一个仿射变换或者仿射映射(来自拉丁语,affine,“和…相关”)由一个非奇异的线性变换(运用一次函数进行的变换)接上一个平移变换组成。”在我的代码中我使用了openCV的仿射变换函数CV::warpAffine()进行了仿射变换,它不是openCV中唯一一个仿射变换函数,但是它可以设置插值方式,并且支持四边形仿射变换,功能很强大,我就决定了使用它了。在第一次旋转时你要首先将旋转后的图像大小计算出来,然后生成一个临时图像,将原图像拷贝到临时图像的中心,再进行旋转,在可以避免缺失图像边角。在第二次旋转时可以直接旋转,但是旋转后你要将原图像外围的图像扣掉,那就要你设置一个矩形区域,然后将原图抠出来。最后就是每次试验设置一个参数就是插值方法,每次保存两个矩阵,原图像矩阵和旋转后的矩阵。其次补充一下matlab编程这部分,为了得到很好的视觉效果,我花了很长时间在绘制一个直方图上。请看实验结果。嘿嘿。
实验结果及其分析:

图1,原图显示 图2,双线性插值第一次变换后的图像
图3,双线性插值第二次变换后的图像
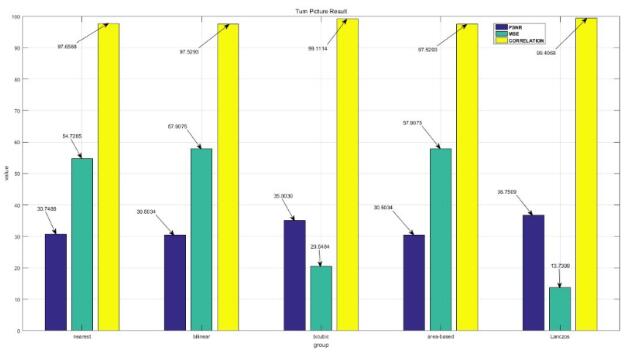
图4,实验结果图
试验结果分析,由图4可以看出,兰索思插值的效果最好,好于双三次插值,双三次插值好于双线性插值,双线性插值好于最近邻插值,最近邻插值和基于区域的插值一样,是效果最差的插值方式。
附件:C++
1 //opencv版本:OpenCV2.7.13 2 //VS版本:VS2015 3 //Author:zqs 4 //time:2018-0322 5 //name:turn picture 6 7 #include<iostream> 8 #include<opencv2/imgproc/imgproc.hpp> 9 #include<opencv2/highgui/highgui.hpp> 10 #include<math.h> 11 #include<fstream> 12 #include<string> 13 14 using namespace std; 15 using namespace cv; 16 17 #define SCALE 1 //缩放比例 18 #define pi 3.1415926 19 20 /* 21 //interpolation seting,if set '0' it is nearest neighbor interpolation,if set '1' it is bilinear interpolation, 22 //if set '2' it is bicubic interpolation,if set '3' it is area-based (or super) interpolation, 23 //if set '4' it is Lanczos interpolation over 8x8 neighborhood. 24 */ 25 #define interpolation 1 26 27 Mat turn_picture(Mat src,int angle,int _interpolation) 28 { 29 Mat dst;//输出旋转后的图像 30 double angle2 = angle * pi / 180; 31 double w = 0., h = 0., w_r = 0., h_r = 0.; 32 33 h = src.rows; 34 w = src.cols; 35 w_r = w*cos(angle2) + h*sin(angle2);//输出图像的宽度或高度 36 h_r = h*cos(angle2) + w*sin(angle2);//为了保证无论如何旋转都能放下 37 38 //建立临时图像,长宽都是源图像的对角线长度,将源图像复制到临时图像的中心后再变换 39 Mat tempImg(w_r, h_r, src.type(), Scalar(0)); 40 //临时图像,大小和输出图像一样大 41 int ROI_x = w_r / 2 - src.cols / 2;//ROI矩形左上角的x坐标 42 int ROI_y = h_r / 2 - src.rows / 2;//ROI矩形左上角的y坐标 43 Rect ROIRect(ROI_x, ROI_y, src.cols, src.rows);//ROI矩形 44 Mat tempImgROI2(tempImg, ROIRect);//tempImg的中间部分 45 src.copyTo(tempImgROI2);//将原图复制到tempImg的中心 46 47 Point2f center(w_r / 2, h_r / 2);//旋转中心 48 Mat M = getRotationMatrix2D(center, angle, SCALE);//计算旋转的仿射变换矩阵 49 50 //输出看看算出的矩阵是什么 51 cout << "变换矩阵:" << endl; 52 cout << M.at<double>(0, 0) << "," << M.at<double>(0, 1) << "," << M.at<double>(0, 2) << "," << endl; 53 cout << M.at<double>(1, 0) << "," << M.at<double>(1, 1) << "," << M.at<double>(1, 2) << "," << endl; 54 55 warpAffine(tempImg, dst, M, Size(w_r, h_r), interpolation);//仿射变换 56 57 return dst; 58 } 59 Mat turn_picture_2(Mat src_src ,Mat src, int angle, int _interpolation) 60 { 61 Mat dst_2;//输出旋转后的图像 62 double w = 0., h = 0.; 63 64 h = src.rows; 65 w = src.cols; 66 67 Point2f center(w / 2, h / 2);//旋转中心 68 Mat M = getRotationMatrix2D(center, angle, SCALE);//计算旋转的仿射变换矩阵 69 70 //输出看看算出的矩阵是什么 71 cout << "变换矩阵:" << endl; 72 cout << M.at<double>(0, 0) << "," << M.at<double>(0, 1) << "," << M.at<double>(0, 2) << "," << endl; 73 cout << M.at<double>(1, 0) << "," << M.at<double>(1, 1) << "," << M.at<double>(1, 2) << "," << endl; 74 75 warpAffine(src, dst_2, M, Size(w, h), interpolation);//仿射变换 76 77 int ROI_x = w / 2 - src_src.cols / 2;//ROI矩形左上角的x坐标 78 int ROI_y = h / 2 - src_src.rows / 2;//ROI矩形左上角的y坐标 79 Rect ROIRect(ROI_x, ROI_y, src_src.cols, src_src.rows);//ROI矩形 80 Mat tempImgROI2(dst_2, ROIRect);//dst_2的中间部分 81 cout << tempImgROI2.cols << endl; 82 cout << tempImgROI2.rows << endl; 83 return tempImgROI2; 84 } 85 86 void store_data(Mat &image, string txt_name) 87 { 88 ofstream outfile; 89 outfile.open(txt_name + ".txt"); //存放数据的文件名 90 91 Mat input_image = image.clone();//复制实参到临时变量 92 int n_r = input_image.rows; // 行数 93 //列数*通道数等于每一行元素的个数 94 int n_c = input_image.cols * input_image.channels(); 95 for (int j = 0; j<n_r; j++) 96 { 97 uchar* data = input_image.ptr<uchar>(j); 98 for (int i = 0; i<n_c; i++) 99 { 100 if (outfile.is_open()) 101 { 102 outfile << (int)data[i] << ","; //程序中处理的数据 103 //outfile.close(); 104 } 105 else 106 { 107 cout << "不能打开文件!" << endl; 108 } 109 //cout << (int)data[i] << ","; 110 } 111 if (outfile.is_open()) 112 { 113 outfile << endl; //message是程序中处理的数据 114 //outfile.close(); 115 } 116 else 117 { 118 cout << "不能打开文件!" << endl; 119 } 120 //cout << endl; 121 } 122 outfile.close(); 123 } 124 125 int main() 126 { 127 Mat src = imread("Chapter2_1.pgm", 0); 128 string txt_src = "Chapter2_1_interpolation_" + to_string(interpolation); 129 string txt_turn_picture = "turn_picture_interpolation_" + to_string(interpolation); 130 131 cout << src.cols << endl; 132 cout << src.rows << endl; 133 134 store_data(src, txt_src); 135 136 int angle_1 = 15;//旋转角度(正值表示逆时针旋转) 137 int angle_2 = -15; 138 //显示 139 imshow("src", src); 140 imshow("turn picture", turn_picture(src,angle_1,interpolation)); 141 142 imshow("turn picture_2", turn_picture_2(src,turn_picture(src, angle_1, interpolation), angle_2, interpolation)); 143 144 store_data(turn_picture_2(src, turn_picture(src, angle_1, interpolation), angle_2, interpolation), txt_turn_picture); 145 146 waitKey(0); 147 return 0; 148 }
附件:matlab
% by zqs
% turn picture
% 2018-3-22
%interpolation seting,if set '0' it is nearest neighbor interpolation,if set '1' it is bilinear interpolation,
%if set '2' it is bicubic interpolation,if set '3' it is area-based (or super) interpolation,
%if set '4' it is Lanczos interpolation over 8x8 neighborhood.
clc;
clear;
close all;
num_bins = 5;
num_methods = 3;
I_0 = load('Chapter2_1_interpolation_0.txt');
I_1 = load('turn_picture_interpolation_0.txt');
r_0 = corrcoef(I_0,I_1);
[psnr_0,mse_0] = psnr_mse(I_0,I_1);
I_2 = load('Chapter2_1_interpolation_1.txt');
I_3 = load('turn_picture_interpolation_1.txt');
r_1 = corrcoef(I_2,I_3);
[psnr_1,mse_1] = psnr_mse(I_2,I_3);
I_4 = load('Chapter2_1_interpolation_2.txt');
I_5 = load('turn_picture_interpolation_2.txt');
r_2 = corrcoef(I_4,I_5);
[psnr_2,mse_2] = psnr_mse(I_4,I_5);
I_6 = load('Chapter2_1_interpolation_3.txt');
I_7 = load('turn_picture_interpolation_3.txt');
r_3 = corrcoef(I_6,I_7);
[psnr_3,mse_3] = psnr_mse(I_6,I_7);
I_8 = load('Chapter2_1_interpolation_4.txt');
I_9 = load('turn_picture_interpolation_4.txt');
r_4 = corrcoef(I_8,I_9);
[psnr_4,mse_4] = psnr_mse(I_8,I_9);
% bins data
data = zeros(num_bins, num_methods);
data(1,1) = psnr_0;
data(2,1) = psnr_1;
data(3,1) = psnr_2;
data(4,1) = psnr_3;
data(5,1) = psnr_4;
data(1,2) = mse_0;
data(2,2) = mse_1;
data(3,2) = mse_2;
data(4,2) = mse_3;
data(5,2) = mse_4;
data(1,3) = r_0(1,2)*100;
data(2,3) = r_1(1,2)*100;
data(3,3) = r_2(1,2)*100;
data(4,3) = r_3(1,2)*100;
data(5,3) = r_4(1,2)*100;
% draw the graph
figure;
handle_bar = bar(data);
ax = gca;
title('Turn Picture Result');
ax.YGrid = 'on';
ax.XGrid = 'on';
ylabel('value');
xlabel('group');
leg_handle = legend('f{}PSNR', 'f{}MSE', 'f{}CORRELATION', 'Location', 'northeast');
% figure position and size : [left bottom width height]
set(gcf, 'Position', [100, 500, 400, 260]);
name = {'nearest', 'bilinear', 'bicubic', 'area-based', 'Lanczos'};
set(gca, 'XTickLabel', name);
% Place text atop the bar
function [PSNR,MSE] = psnr_mse(X,Y)
if any(size(X)~=size(Y))
error('The input size is not equal to each other!');
end
D = X-Y;
MSE = sum(D(:).*D(:))/numel(X);
PSNR = 10*log10(255^2/MSE);
end