一、引言
哈喽大家好,今天要给大家讲的是Floyd算法。在那之前,大家还记得我们上一章讲的内容吗,就是那个Dijkstra算法,用来解决从A点到B点的最短路径问题。我们还给出了Matlab代码。Floyd算法也是用来处理最短路径问题的。它的理念跟Dijkstra有点不一样,但是最终的结果是一样的。Floyd算法主要是用到了动态规划的思想。在这里博主不打算讲到很抽象很高深的东西(毕竟博主也不是专业的),仅仅通过比较通俗易懂的方式来给大家讲解这个算法的思想(如果有问题大家帮忙指出来哈)。本文的图片和思想,借用了https://blog.csdn.net/qq_34374664/article/details/52261672的博文(图片画得好好,有谁知道是用什么软件画的吗,博主也想学一学)。本篇的主要思想来自那篇博文,因此会有很多类似的,但博主还是想以自己的理解来解释Floyd算法的理念。好了我们开始吧...
二、Floyd算法
首先,大家看上面的图,暑假,小哼准备去一些城市旅游。有些城市之间有公路,有些城市之间则没有。为了节省经费以及方便计划旅程,小哼希望在出发之前知道任意两个城市之前的最短路程。我们用1-4来表示4个地点,并用箭头和箭头上的数字来表示一个地点到另一个地点的距离(注意,有些路是单向的)。这样就得到下图
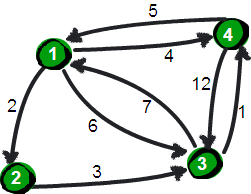
现在,我们希望能求解出任意两点的最短路径及其距离。
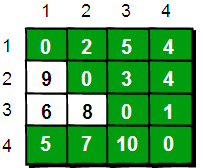
好了,为了求解这个问题,我们先用一个二维的数组A来存储我们图的信息。如下图(怎么看这个图下面解释)
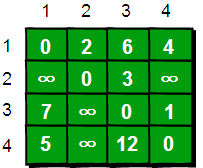
这个是怎么数组填写出来的呢,举例来讲吧,比如1号城市到2号城市的路程为2,则设A(1, 2)的值为2。2号城市无法到达4号城市,则设置A(2, 4)的值为$\infty$。另外此处约定一个城市自己是到自己的也是0,例如A(1, 1)为0。
现在问题是,如何求解任意两个点的最短距离。我们可以这样想,我们假设第$i$点和第$j$点的距离,应该就包括两种情况:
1. $i$和$j$之间是直接相连的(即$i \rightarrow j$);
2. $i$和$j$之间还有其他端点(即$i \rightarrow \cdot \cdot \cdot \rightarrow j$);
上面两句话什么意思呢,我们先看下面这张图:
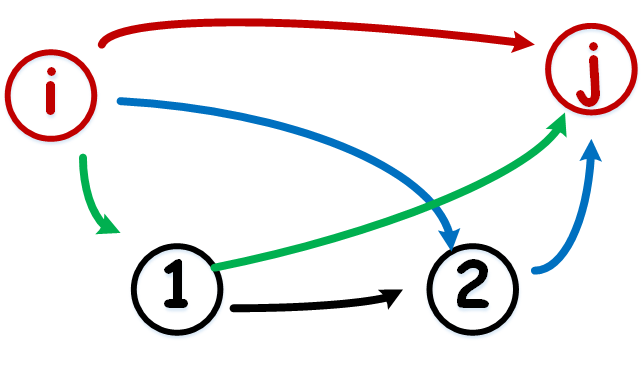
我们现在比如说从地点$i$到地点$j$,我们可以直接走红色路线,即$i \rightarrow j$;或者,走经过1(或者2或者经过1和2)的路线。即从地点$i$开始,先经过其他地点,再从其他地点到$j$,即$i \rightarrow \cdot \cdot \cdot \rightarrow j$
那么,哪个才是最短距离呢。接下来就是算法的核心和重点了,大家注意啦!!
当任意两点之间不允许经过第三个点时,这些城市之间最短路程就是初始路程,如下
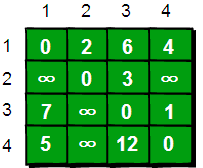 (1)现在,如果我只允许经过1号顶点,求任意两点之间的最短路程,该怎么求呢?
(1)现在,如果我只允许经过1号顶点,求任意两点之间的最短路程,该怎么求呢?
由于只允许经过1号顶点,那任意两点的路线不外乎只有两种,即:
1. $i \rightarrow 1 \rightarrow j$
2. $i \rightarrow j$
要求最短路程,只要比较这两个路线距离的大小即可。就是:
即
A(i, j) = min [A(i, j), A(i, 1) + A(1, j)]
在只允许经过1号顶点的情况下,任意两点之间的最短路程更新为:
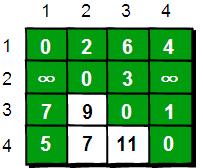
通过上图我们发现:在只通过1号顶点中转的情况下,3号顶点到2号顶点(A(3, 2))、4号顶点到2号顶点(A(4, 2))以及4号顶点到3号顶点(A(4, 3))的路程都变短了。
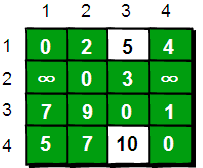
(2)接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短路程。如何做呢?
可以写出公式:A(i, j ) = A(i, 1) + A(1, 2) + A(2, j)
根据(1)我们已经求出A(i, 1) + A(1, 2) = min [A(i, 2), A(i, 1) + A(1, 2)]。
故我们只需要在只允许经过1号顶点时任意两点的最短路程的结果下,再判断如果经过2号顶点是否可以使得$i$号顶点到$j$号顶点之间的路程变得更短。
即
A(i, j) = min [A(i, j), A(i, 2) + A(2, j)]
在只允许经过1和2号顶点的情况下,任意两点之间的最短路程更新为:
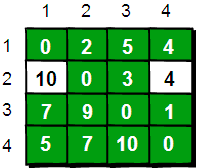
function [D, path] = floyd(A)
% [D,PATH] = FLOYD(A)
% returns the distance and path between the start node and the end node.
%
% A: adjcent matrix
%% 初始化
%节点的数量n
D = A;
n = length(D);
path = zeros(n, n);
%% 初始化path
for i = 1: n
for j = 1: n
if D(i, j) ~= inf
path(i, j) = j;
end
end
end
%% 记录最短路径与最短距离
for k = 1: n
for i = 1: n
for j = 1: n
if D(i, j) > D(i, k) + D(k, j)
D(i, j) = D(i, k) + D(k, j);
path(i, j) = path(i, k);
end
end
end
end