一、引言
在上一个篇章中,我们用遗传算法来计算一个一元函数的最大值,但是,有人会讲,这样是不是有些大材小用了,明明我可以用更少的代码来实现求最大值的功能。确实,将遗传算法用在那里确实大材小用了,但是,博主的目的并不是为求最大值,而是为了给大家展示,遗传算法是一种可行的算法,并且博主编写的matlab代码是可行的。现在,我们就要利用上一篇写的代码作为基本代码,来解决本篇的问题。放心,本篇的问题可不是用普通的方法就能就解决的。遗传算法的春天终于来了。让我们开始吧。。
二、问题描述和建模
负载均衡调度问题:假设有N个任务,需要负载均衡器分配给M个服务器节点去处理。每个任务的任务长度、每台服务器节点(下面简称“节点”)的处理速度已知,请给出一种任务分配方式,使得所有任务的总处理时间最短。
好,那么现在题目有了,但是我们要想办法对题目进行数学建模。显然,我们需要2个矩阵,一个存放任务(含任务数量、任务长度),一个存放服务器节点(含节点数量、处理速度)。
(1)任务长度矩阵(简称:任务矩阵)
我们将所有任务的任务长度用矩阵tasks表示,其中tasks(i)中的i表示任务的编号,tasks(i)表示任务i的任务长度。比如
tasks = [2, 4, 6, 8]
表明,任务1的长度是2;任务2的长度是4,以此类推。
(2)节点处理速度矩阵(简称:节点矩阵)
我们将所有服务器节点的处理速度用nodes表示,其中nodes(i)中的i表示节点的编号,nodes(i)表示节点j的处理速度。比如
nodes = [2, 1]
表明,节点1的速度是2;节点2的速度是1,以此类推。
(3)任务处理时间矩阵
当任务矩阵task和节点矩阵nodes确定下来后,那么所有任务分配给所有节点的任务处理时间就可以确定了,我们用矩阵timeMat来存所有节点的任务处理时间,那么timeMat(i, j)表示任务i分配给节点j处理所需的时间,它通过以下公式计算:
timeMat(i, j) = task(i) / nodes(j);
有了上面三个矩阵后,我们就算是成功将题目用数学的方式描述出来了。
我们用matlab代码创建一个createData.m文件,用来对题目进行建模并且保存数据。如下:
%% I. 清空自变量
clear all
clc
%% II. 题目建模
% 参数定义
taskNum = 100; % 任务数量
taskLengthRange = [10, 100]; % 任务长度范围
nodeNum = 10; % 节点数量
nodeSpeedRange = [10, 100]; % 节点长度范围
tasks = initRandomMat(taskNum, taskLengthRange); % 构建任务矩阵(含任务数量和任务长度)
nodes = initRandomMat(nodeNum, nodeSpeedRange); % 构建节点矩阵(含节点数量和节点处理速度)
timeMat = zeros(taskNum, nodeNum); % 构建处理时间矩阵
for i = 1: taskNum
for j = 1: nodeNum
timeMat(i, j) = tasks(1, i) / nodes(1, j);
end
end
%% III. 数据保存
save('data', 'tasks', 'nodes', 'timeMat');
其中initRandomMat()函数代码如下:
% [name] -- initRandomMat(初始化随机矩阵)
% [function]--
% [input] -- length (数组的长度)
% -- range (数组元素的取值范围range(1) to range(2))
% [output] -- randomMat
function randomMat = initRandomMat(length, range)
randomMat = zeros(1, length);
for i = 1: length
randomMat(1, i) = round(rand() * (range(2) - range(1)) + range(1));
end
三、遗传算法解决问题
还是老样子,我们先回顾下遗传算法的步骤,如下:
1. 种群初始化
2. 计算每个种群的适应度值
3. 选择(Selection)
4. 交叉(Crossover)
5. 变异(Mutation)
6. 重复2-5步直至达到进化次数
正如我们上一篇所说,为了让我们的代码有更好的包容性,我们需要先写几个函数包,到时再main.m里面引用,就很方便了。
(1)种群初始化函数popInit(),能根据提供的种群大小和染色体长度产生初始的种群。代码如下:
% [name] -- popInit(种群初始化函数) % [function]-- 构建种群矩阵,其中行数为种群个数,列数为染色体长度(即基因的个数),并随机分配染色体的样式 % [input] -- 1. popSize(种群大小/个数) % -- 2. cLength(染色体长度) % -- 3. range (染色体上基因的数值范围0 - range) % [output] -- popMat(种群矩阵) function popMat = popInit(popSize, cLength, range) popMat = zeros(popSize, cLength); % 预分配内存 for i = 1: popSize for j = 1: cLength popMat(i, j) = ceil(rand() * range); % rand产生(1,range)之间的随机数 end end clear i; clear j;
(2)计算每个种群的适应度值函数getfitnessValue()。代码如下:
% [name] -- getfitnessValue(计算种群个体适应度值)
% [function]-- 根据不同的题目要求,设计适应度方程计算的算法
% -- 在实际的负载均衡调度中,各个节点的任务处理是并行计算的,所以,所有任务的完成时间应该是所有节点任务完成时间的最大值,并非所有任务完成时间的总和。
% [input] -- timeMat (时间处理矩阵) -- timeMat(i, j): 第i个任务分配到第j个节点,需要的处理时间
% -- popMat (种群矩阵) -- popMat(i, j): 第i个染色体上, 第j个任务分配到的节点标号
% -- nodeNumMax (节点的最大标号)
% [output] -- fitValMat(每个染色体的适应度值)
function fitnessValueMatrix = getfitnessValue(popMat, timeMat, nodeNumMax)
[popSize, cLength] = size(popMat); % 获取种群的数目(行)和染色体长度(列)
fitnessValueMatrix = zeros(popSize, 1); % 初始化适应度矩阵 % 最大的节点标号
for i = 1: popSize
maxLength = eps; % 大于0的最小正数
for nodeIndex = 1: nodeNumMax
sumLength = 0; % 清零
for j = 1: cLength
if popMat(i, j) == nodeIndex
sumLength = sumLength + timeMat(j, nodeIndex);
end
end
if sumLength > maxLength
maxLength = sumLength;
end
end
fitnessValueMatrix(i) = maxLength;
end
clear i;
clear j;
clear nodeIndex;
(3)选择函数selection(),可以对种群进行选择,具体算法和代码如下:
% [name] -- selection(选择操作)
% [function]-- 采用轮盘赌的一个形式来进行选择,增加不确定性,这样种群就不容易趋向局部最优
% [input] -- 1. fitnessValueMatrix (适应度值矩阵)
% -- 2. popMat(未选择的种群矩阵)
% -- 3. type -- 1: 保留亲代最优个体
% 0: 不保留亲代最优个体
% [output] -- updatedPopMat(经选择后的种群矩阵)
function updatedPopMat = selection(fitnessValueMatrix, popMat, type)
[popSize, cLength] = size(popMat);
updatedPopMat = zeros(popSize, cLength);
fitnessValueMatrix = 100 ./ fitnessValueMatrix;
% 剔除适应值为负的种群,使其适应值为0
for i = 1: popSize
if fitnessValueMatrix(i, 1) < 0
fitnessValueMatrix(i, 1) = 0;
end
end
% 轮盘赌算法
P = fitnessValueMatrix / sum(fitnessValueMatrix);
Pc = cumsum(P);
for i = 1: popSize
index = find(Pc >= rand);
updatedPopMat(i, :) = popMat(index(1), :);
end
% 是否要保留亲本适应度值最高的,若是,则type = 1,否则为0
if type
[~, bestIndex] = max(fitnessValueMatrix);
updatedPopMat(popSize, :) = popMat(bestIndex, :); % 将亲代最优染色体放到子代的最后一个个体中
end
clear i;
clear j;
(4)交叉函数crossover(),可以对种群进行交叉,交叉的方式又分为单点交叉和多点交叉,根据输入不同的参数来选择不同的实现方式,具体算法和代码如下:
% [name] -- crossover(交叉操作)
% [function]-- 选定交叉点并进行互换
% [input] -- 1. popMat (未交叉的种群矩阵)
% -- 2. type -- 1: 单点交叉
% -- 2: 多点交叉
% -- 3. crossrate (交叉率) -- 建议值为0.6
% [output] -- updatedPopMat(经交叉后的种群矩阵)
function updatedPopMat = crossover(popMat, type, crossrate)
[popSize, cLength] = size(popMat);
if type == 1
% 单点交叉
for i = 1: 2: popSize
if crossrate >= rand
crossPosition = round(rand() * (cLength - 2) + 2); % 随机获取交叉点,去除0和1
% 对 crossPosition及之后的二进制串进行交换
for j = crossPosition: cLength
temp = popMat(i, j);
popMat(i, j) = popMat(i + 1, j);
popMat(i + 1, j) = temp;
end
end
end
updatedPopMat = popMat;
elseif type == 2
% 多点交叉
for i = 1: 2: popSize
if crossrate >= rand
crossPosition1 = round(rand() * (cLength - 2) + 2); % 第一个交叉点
crossPosition2 = round(rand() * (cLength - 2) + 2); % 第二个交叉点
first = min(crossPosition1, crossPosition2);
last = max(crossPosition1, crossPosition2);
for j = first: last
temp = popMat(i, j);
popMat(i, j) = popMat(i + 1, j);
popMat(i + 1, j) = temp;
end
end
end
updatedPopMat = popMat;
else
h = errordlg('type的类型只能为1(单点交叉)或者2(多点交叉)', '进行交叉时发生错误');
end
clear i;
clear j;
(5)变异函数mutation(),可以对种群进行变异,具体算法和代码如下:
% [name] -- mutation(变异操作) % [function]-- 单点变异:随机选择变异点,将其变为0或1 % [input] -- 1. popMat (未交叉的种群矩阵) % -- 2. mutateRate (交叉率) -- 建议值为0.1 % -- 3. randValur (变异后的随机数范围0-randValue) % [output] -- updatedPopMat(经交叉后的种群矩阵) function updatedPopMat = mutation(popMat, mutateRate, randValue) [popSize, cLength] = size(popMat); for i = 1: popSize if mutateRate >= rand mutatePosition = ceil(rand() * cLength); % 随机获取交叉点,去除0 % 对mutatePosition点进行变异 popMat(i, mutatePosition) = ceil(rand() * randValue); end end updatedPopMat = popMat; clear i; clear j;
(6)画图函数plotGraph:用于直观的显示在进化的过程中,种群平均总处理时间的变化。代码如下:
% [name] -- plotGraph(画图)
% [function]-- 直观的展示在进化过程中,平均适应度值的趋势变化
% [input] -- 1. generationTime(进化次数)
% 2. fitnessAverageValueMatrix(平均适应度值矩阵)
% [output] -- none
function plotGraph(fitnessAverageValueMatrix, generationTime)
x = 1: 1: generationTime;
y = fitnessAverageValueMatrix;
plot(x, y);
xlabel('迭代次数');
ylabel('平均总处理时间');
title('种群平均总处理时间的进化曲线');
好了,至此,我们就完成了解决本题目需要的函数块。接下来,我们只需要编写主函数main.m,针对本章的题目,对其进行求解即可。代码如下:
%% I. 清空变量
clear all
clc
%% II. 导入数据和参数初始化
%导入参数数据
tasks = load('data', 'tasks'); % 导入任务矩阵(含任务数量和任务长度)
tasks = tasks.tasks; % 导入的是struct格式,因此要再多此一步
nodes = load('data', 'nodes'); % 导入节点矩阵(含节点数量和节点处理速度)
nodes = nodes.nodes;
timeMat = load('data', 'timeMat'); % 导入处理时间矩阵
timeMat = timeMat.timeMat;
taskNum = length(tasks); % 任务数量
nodeNum = length(nodes); % 节点数量
iteratorNum = 1000; % 迭代次数
popSize = 300; % 种群大小(染色体数量)
crossRate = 0.6; % 交叉概率
mutateRate = 0.01; % 变异概率
fitnessAverageValueMatrix = zeros(iteratorNum, 1); % 每代平均适应度值
fitnessBestValueMatrix = zeros(iteratorNum, 1); % 每代最优适应度值
bestIndividual = zeros(iteratorNum, taskNum); % 每代最佳自变量
%% III. 初始化种群
popMat = popInit(popSize, taskNum, nodeNum);
%% IV. 迭代繁衍获取更好的个体(选择、交叉、变异)
for currentNum = 1: iteratorNum
% 求单个染色体的总处理时间和适应度矩阵
sumTimeMat = getfitnessValue(popMat, timeMat, nodeNum); % 染色体的总处理时间
% 记录当前最好的数据
if currentNum == 1
[~, bestIndex] = min(sumTimeMat);
fitnessBestValueMatrix(currentNum) = min(sumTimeMat);
fitnessAverageValueMatrix(currentNum) = mean(sumTimeMat);
bestIndividual(currentNum, :)= popMat(bestIndex, :); % 最佳适应度值所对应的染色体(分配方案)
else
[~, bestIndex] = min(sumTimeMat);
fitnessBestValueMatrix(currentNum) = min(fitnessBestValueMatrix(currentNum - 1), min(sumTimeMat));
fitnessAverageValueMatrix(currentNum) = mean(sumTimeMat);
if fitnessBestValueMatrix(currentNum) == fitnessBestValueMatrix(currentNum - 1)
bestIndividual(currentNum, :) = bestIndividual(currentNum - 1, :);
elseif fitnessBestValueMatrix(currentNum) == min(sumTimeMat)
bestIndividual(currentNum, :) = popMat(bestIndex, :);
else
h = errordlg('请检查代码', '意外错误');
end
end
if currentNum ~= iteratorNum
% 选择
popMat = selection(sumTimeMat, popMat, 1); % 保留亲代最佳个体
% 交叉
popMat = crossover(popMat, 1, crossRate); % 单点交叉
% 变异
popMat = mutation(popMat, mutateRate, nodeNum);
end
end
%% V. 画图并展示结果
% 画图
plotGraph(fitnessAverageValueMatrix, iteratorNum);
% 展示数据
disp 最短处理时间
fitnessBestValueMatrix(currentNum, 1)
plan = bestIndividual(currentNum, :);
运行上述程序,可以得到:
ans =
9.5278
可以得知,经过我们的遗传算法,可以设计出一套方案,让总处理时间大大减小(不能保证是最小,但接近最小)。下面大家可以看看,随着迭代次数的增加,遗传算法对方案的优化进而平均总处理时间的变化。
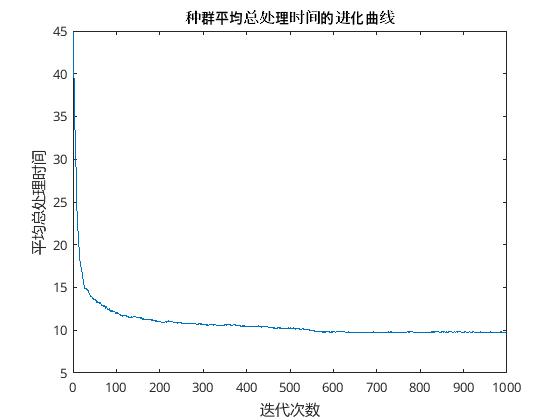
可以看到,随着迭代次数的增加,平均总处理时间从30多降到最后的9点多。