题目说明:
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。排序n 个项目要Ο(n log n)次比较。
题目解析:
1、堆
堆实际上是一棵完全二叉树,在第一个元素的索引为0的情形中满足特性:
性质一:索引为i的左孩子的索引是 (2*i+1);
性质二:索引为i的左孩子的索引是 (2*i+2);
性质三:索引为i的父结点的索引是 int((i-1)/2);
最大堆:任何父节点的关键字不小于其左右孩子节点的关键字(Key[i]>=Key[2i+1]&&key>=key[2i+2]);
最小堆:任何父节点的关键字不小于其左右孩子节点的关键字(Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]);
由上述性质可知最大堆的堆顶的关键字肯定是所有关键字中最大的,最小堆的堆顶的关键字是所有关键字中最小的。
如下面最大堆和最小堆
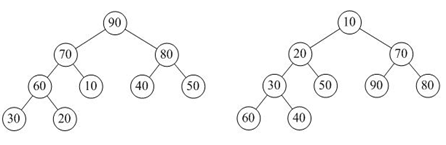
2、堆排序
利用最大堆(最小堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
其基本思想为(最大堆):
1)将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
操作过程如下:
1)初始化堆:将R[1..n]构造为堆;
2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换,然后将新的无序区调整为新的堆。
因此对于堆排序,最重要的两个操作就是构造初始堆和调整堆,其实构造初始堆事实上也是调整堆的过程,只不过构造初始堆是对所有的非叶节点都进行调整。
程序代码:
#include <gtest/gtest.h> #include <algorithm> using namespace std; #define M_PARENT(i) (i)/2 #define M_LEFT(i) 2*(i)+1 #define M_RIGHT(i) 2*(i+1) template<typename T> void MaxHeapify(T* data, int index, int len) { int l = M_LEFT(index); int r = M_RIGHT(index); int largest; if (l < len && data[l] > data[index]) { largest = l; } else { largest = index; } if (r < len && data[r] > data[largest]) { largest = r; } if (largest != index) { T tmp = data[largest]; data[largest] = data[index]; data[index] = tmp; MaxHeapify(data, largest, len); } } template<typename T> void BuildMaxHeap(T* data, int len) { if (!data || len <= 1) return; for (int i=len/2 + 1; i>=0; --i) { MaxHeapify(data,i,len); } } template<typename T> void HeapSort(T* data, int len) { if (!data || len <= 1) { return; } BuildMaxHeap(data, len); for (int i=len-1; i>=1; --i) { T tmp = data[0]; data[0] = data[i]; data[i] = tmp; MaxHeapify(data,0,--len); } } // Helper function template<typename T> void ShowElem(T& val) { cout << val << " "; } template<typename T> bool Validate(T* data, int len) { for (int i=0; i < len-1; ++i) { if (data[i] > data[i+1]) { return false; } } return true; } TEST(Algo, tHeapSort) { int d1[] = {2,8,7,1,3,5,6,4}; HeapSort(d1, 8); for_each(d1, d1+8, ShowElem<int>); ASSERT_TRUE(Validate(d1,8)); cout << endl; int d2[] = {2}; HeapSort(d2, 1); for_each(d2, d2+1, ShowElem<int>); ASSERT_TRUE(Validate(d2,1)); cout << endl; int d3[] = {2,4,5,6,7,5,2,3,5,7,10,111,2,4,5,6,3,4,5}; HeapSort(d3, 19); for_each(d3, d3+19, ShowElem<int>); ASSERT_TRUE(Validate(d3,19)); cout << endl; }
运行结果:
参考引用:
http://www.cricode.com/2001.html
http://www.cnblogs.com/kaituorensheng/archive/2013/02/22/2922970.html
看书、学习、写代码