CodeForces-1076B Divisor Subtraction 找规律

题目链接：https://vjudge.net/problem/CodeForces-1076B

题意：

题目要求给定一个数，要求每次减去其最小素因数（既是素数又是其因数），问直到n=0需要做几次运算。

分析：

首先如果n为素数，则其最小素因数就是它本身，故第一次运算n:=n-n即得0，只需要一次运算。当n为偶数时，素因子恒为2，故每次减2直到0，所以运算次数为n/2次，当n为奇数是，首先减一次最小素因子，因为最小素因子一定是奇数，故奇-奇=偶，变为偶数后就按上述做法求得运算次数即可。

总结如下：

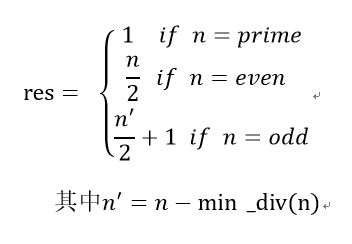
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
typedef long long ll;
using namespace std;
ll n;

bool prime(ll x) {
    for(ll i = 2; i <= sqrt(x); i++) {
        if(x % i == 0)
            return false;
    }
    return true;
}

ll min_div(ll x) {
    for(ll i = 2; i < n; i++) {
        if(x % i == 0)
            return i;
    }
}

int main(void) {
    while(scanf("%lld", &n) == 1) {
        if(prime(n)) {
            printf("1
");
            continue;
        }
        else if(n % 2 == 0) {
            printf("%lld
", n/2);
            continue;
        }
        else {
            n -= min_div(n);
            printf("%lld
", n/2+1);
        }
    }
}