递归式求解

1. 主定理

1.1 主定理介绍

1.2 不能使用主定理的情况

（1）T(n)不是单调函数，(e.g. T(n) = sinx)

（2）f(n)不是多项式函数 (e.g. T(n) = T(n/2) + 2ⁿ)

（3）b不能表示为一个常量（e.g. T(n) = 2T(√n））

1.3 举例说明

(1) T(n) = T(n/2) + 1/2 * n² + n

解：

此时 a = 1, b = 2, f(n) =  1/2*n² + n

故 n^log_ba = n⁰ = 1

f(n) = Ω(n^log_ba+2)，ε=2，且当 C = 1/4时，满足第三种情况的条件

故第三种情况成立，T(n) = θ(n²)

(2) T(n) = 2T(n/4) + √n + 42

解：

此时 a = 2, b = 4, f(n) = √n + 42

故 n^log_ba = n^1/2

所以 f(n) = Θ(n^log_ba)

故第二种情况成立，T(n) = Θ(n^log_ba*logn) = Θ(√n*logn)

(3) T(n) = 3T(n/2) + 3/4*n + 1

解：

此时 a = 3, b = 2, f(n) = 3/4*n + 1

故 n^log_ba = n

所以 f(n) = O(n^{log_ba-(log_ba-1)})，ε = log_ba-1 = log₂3-1 > 0，

故第一种情况成立，T(n) = Θ(n^log_ba) =  Θ(n^log₂3) 

2. 递归树

递归树是一棵结点带权值的树。初始的递归树只有一个结点，它的权标记为T(n)；然后按照递归树的迭代规则不断进行迭代，每迭代一次递归树就增加一层，直到树中不再含有权值为函数的结点（即叶结点都为T(1)T(1)）。下面以递归方程

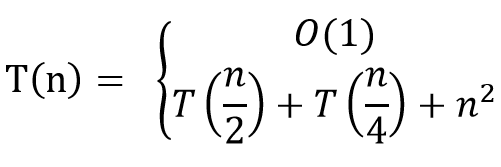
为例讲解递归树。

首先这道题肯定是没法用主定理，所以画递归树：

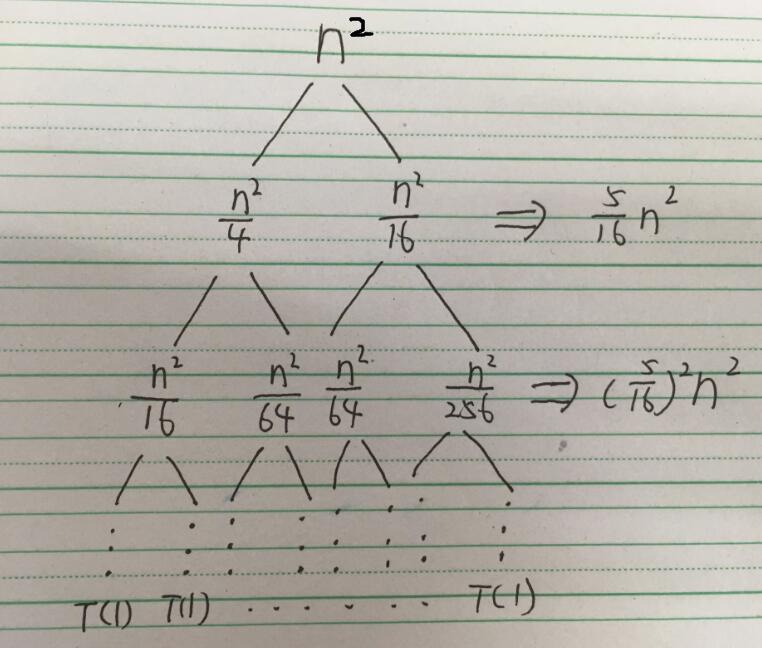
因为每次两个分支大小不相同，故这颗树实际上并不像画出来这样的平衡，故树高度最高为log₂n_，最低为log₄n

我们假设极限树高为log₂n_，即最大高度，且为平衡树，此时可以得到时间复杂度的上界:

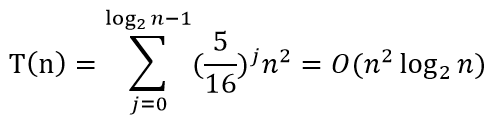
同理当极限树高为log₄n时_，得到时间复杂度的下界：

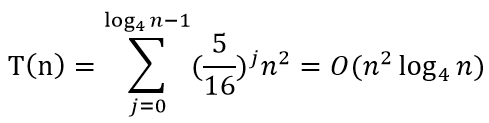
故可知时间复杂度为

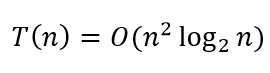
3. 找规律

T(n) = 2T(n-1) + 1（T(1) = 1)

这道题是不是看起来很像高中学的等比数列递推式，是的！

如果方程右端出现T(n-1)这种式子，很有可能是递推式，再观察是等比还是等差数列，这道题很像等比，所以构造

AT(n)+B = 2(T(n-1)+B)

再和原式比较，得A = 1, B = 1，也就是说 T(n) +1 = 2(T(n-1) + 1)

首项为T(1)+1 = 2，所以得通项公式为：

T(n) + 1 = 2*2^n-1 = 2ⁿ

不过对于这类题还有一种更通用的公式很方便：

对于这道题来说，c=1，b=2，g(n)=1，代入方程得：

与前面做法得到得结果相同