51nod 1353 树 | 树形DP好题!
题面
切断一棵树的任意条边,这棵树会变成一棵森林。
现要求森林中每棵树的节点个数不小于k,求有多少种切法。
数据范围:(n le 2000)。
题解
//为什么这道题做的人这么少呢……感觉这道题超级经典,非常符合上周末模拟那种树形DP的套路。会做这道题之后,可以想出许多类似的树形DP。
首先状态很好想:(dp[u][i])表示“以u为根的子树中,与u相连的联通块大小是i,剩下的联通块大小均大于k”的方案数。
下面的题解中,我们设要求的是(dp[u][i]),父亲是u,儿子是v,sze[i]表示以i为根的子树的大小。
为了方便起见,我们画图说明:
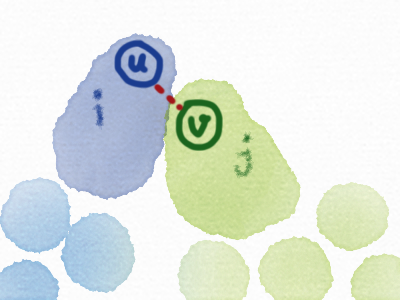
由于u有许多儿子,我们一次只处理一个儿子,处理的时候,就相当于将一堆新的节点(子树v)添加到原有的图。
现在与u相连的联通块大小为i,与j相连的大小为j。显然对于(u, v)之间的这条边,要么切断,要么不切断。上图描述的是切断的情况(这种情况要求j >= k)。显然新的(dp[u][i] += dp[u][i] * dp[v][j])。(注意,等式右边的(dp[u][i])是在联通块中加入子树v之前的答案)。
另一种情况是不切断这条边。如下图:

由于没切断,加入新子树之后,与u相连的联通块的大小由i变成了i + j。
那么显然:(dp[u][i + j] += dp[u][i] * dp[v][j])。(等式右边的dp[u][i]仍是加入子树之前的)。
现在我们连状态转移方程都想好了,写代码是不是就很简单了呢?可能……并不是……(至少对于我来说)
十分需要注意的地方是(dp[u][i])意义的变化。我们必须保证等式右边的(dp[u][i])永远是加入子树之前的答案。例如,对于切断(u, v)这条边的情况,如果我们在u、v没有改变的情况下,直接这样循环:
for r i : 1 -> sze[u]
for j : 1 -> sze[v]
dp[u][i] += dp[u][i] * dp[v][j]
显然是不行的。因为等式右侧的(dp[u][i])一经修改就不是“加入子树v之前的”了。
一种合理的解决方案是用(dp[v][0])表示与v相连的联通块大小大于等于k的所有方案数之和,这样对于切断(u, v)的情况,直接(dp[u][i] = dp[u][i] * dp[v][0])即可,前提是在这一步之前(dp[u][i])没有更新过。所以我们接下来让更小的i中的“不切断的情况”来更新这里的(dp[u][i])。这里直接(dp[u][i + j] += dp[u][i] * dp[v][j])是没有问题的。
啊对了!这个代码看起来是(O(n^3))的啊!
……但其实由于每次两层循环i、j分别枚举了子树u(的已知部分)和子树v的点,时间复杂度增加了sze[u] * sze[v],相当于枚举了每一对点,那么总计每一对点只被枚举了一次。总计(O(n^2))。
代码:
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned long long ll;
#define INF 0x3f3f3f3f
#define enter putchar('
')
#define space putchar(' ')
template <class T>
bool read(T &x){
char c;
bool op = 0;
while(c = getchar(), c < '0' || c > '9')
if(c == '-') op = 1;
else if(c == EOF) return 0;
x = c - '0';
while(c = getchar(), c >= '0' && c <= '9')
x = x * 10 + c - '0';
if(op) x = -x;
return 1;
}
template <class T>
void write(T x){
if(x >= 10) write(x / 10);
putchar('0' + x % 10);
}
const int N = 2005, P = 1e9+7;
int n, k, sze[N];
int ecnt, adj[N], nxt[2*N], go[2*N];
ll dp[N][N], ans;
void add(int u, int v){
go[++ecnt] = v;
nxt[ecnt] = adj[u];
adj[u] = ecnt;
}
void dfs(int u, int pre){
dp[u][1] = sze[u] = 1;
for(int v, e = adj[u]; e; e = nxt[e])
if(v = go[e], v != pre){
dfs(v, u);
for(int i = sze[u]; i; i--){
for(int j = 1; j <= sze[v]; j++)
dp[u][i + j] = (dp[u][i + j] + dp[v][j] * dp[u][i]) % P;
dp[u][i] = dp[u][i] * dp[v][0] % P;
}
sze[u] += sze[v];
}
for(int i = k; i <= sze[u]; i++)
dp[u][0] = (dp[u][0] + dp[u][i]) % P;
}
int main(){
read(n), read(k);
for(int i = 1, u, v; i < n; i++)
read(u), read(v), add(u, v), add(v, u);
dfs(1, 0);
for(int i = k; i <= n; i++)
ans = (ans + dp[1][i]) % P;
write(ans), enter;
return 0;
}