51nod 1589 移数博弈
题面
给出一个序列a,长度 n <= 10^7, a[i] <= 10^7
求每个长度 >= 2 的区间的最大值*次大值 之和。
题解
主要思路是求每个元素作为次大值做了多少贡献。
对于一个元素 a[i], 设从i向左走能找到的第一个比a[i]大的位置为l[i], 第二个比a[i]大的位置为ll[i], 向右走能找到的第一个比a[i]大的位置为r[i], 第二个为rr[i]。
a[i]作为次大值的时候,区间最大值要么是a[l[i]], 要么是a[r[i]]。
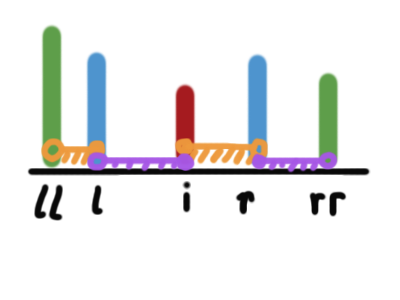
如上图(竖直柱表示不同大小的数,之前未画出的均比a[i]小),若a[l[i]]是最大值,那么区间左、右端点应分别在橙色区间的两部分中;否则应该在紫色区间的两部分中。
对应计算区间数量求贡献即可。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
char c;
bool op = 0;
while(c = getchar(), c < '0' || c > '9')
if(c == '-') op = 1;
x = c - '0';
while(c = getchar(), c >= '0' && c <= '9')
x = x * 10 + c - '0';
if(op) x = -x;
}
template <class T>
void write(T x){
if(x < 0) x = -x, putchar('-');
if(x >= 10) write(x / 10);
putchar('0' + x % 10);
}
const int N = 1e7 + 5, P = 1e9 + 7;
int n, A, B, p, a[N], b[N], cnt[N], pre[N], nxt[N];
ll ans;
//b[i]是a中排名第i的元素的位置
int main(){
read(n), read(a[0]), read(A), read(B), read(p);
for(int i = 1; i <= n; i++)
a[i] = ((ll)a[i - 1] * A + B) % p, cnt[a[i]]++;
a[0] = 0;
for(int i = 1; i <= 1e7; i++)
cnt[i] += cnt[i - 1];
for(int i = n; i; i--)
b[cnt[a[i]]--] = i;
for(int i = 0; i <= n + 1; i++)
pre[i] = i - 1, nxt[i] = i + 1;
pre[0] = 0, nxt[n + 1] = n + 1;
for(int i = 1; i <= n; i++){
ans = (ans + (ll) a[b[i]] * a[pre[b[i]]] % P
* (pre[b[i]] - pre[pre[b[i]]]) % P
* (nxt[b[i]] - b[i]) % P) % P;
ans = (ans + (ll) a[b[i]] * a[nxt[b[i]]] % P
* (nxt[nxt[b[i]]] - nxt[b[i]]) % P
* (b[i] - pre[b[i]]) % P) % P;
pre[nxt[b[i]]] = pre[b[i]];
nxt[pre[b[i]]] = nxt[b[i]];
}
write(ans), putchar('
');
return 0;
}