题目:https://codeforces.com/contest/1200/problem/C
Amugae is in a very large round corridor. The corridor consists of two areas. The inner area is equally divided by nn sectors, and the outer area is equally divided by mm sectors. A wall exists between each pair of sectors of same area (inner or outer), but there is no wall between the inner area and the outer area. A wall always exists at the 12 o'clock position.
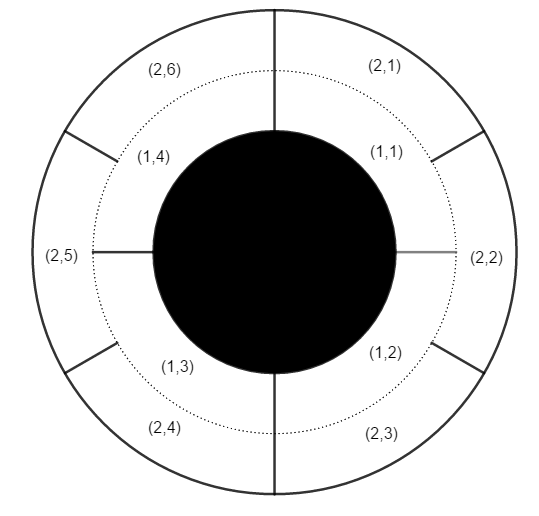
The inner area's sectors are denoted as (1,1),(1,2),…,(1,n)(1,1),(1,2),…,(1,n) in clockwise direction. The outer area's sectors are denoted as (2,1),(2,2),…,(2,m)(2,1),(2,2),…,(2,m) in the same manner. For a clear understanding, see the example image above.
Amugae wants to know if he can move from one sector to another sector. He has qq questions.
For each question, check if he can move between two given sectors.
The first line contains three integers nn, mm and qq (1≤n,m≤10181≤n,m≤1018, 1≤q≤1041≤q≤104) — the number of sectors in the inner area, the number of sectors in the outer area and the number of questions.
Each of the next qq lines contains four integers sxsx, sysy, exex, eyey (1≤sx,ex≤21≤sx,ex≤2; if sx=1sx=1, then 1≤sy≤n1≤sy≤n, otherwise 1≤sy≤m1≤sy≤m; constraints on eyey are similar). Amague wants to know if it is possible to move from sector (sx,sy)(sx,sy) to sector (ex,ey)(ex,ey).
For each question, print "YES" if Amugae can move from (sx,sy)(sx,sy) to (ex,ey)(ex,ey), and "NO" otherwise.
You can print each letter in any case (upper or lower).
4 6 3 1 1 2 3 2 6 1 2 2 6 2 4
YES NO YES
Example is shown on the picture in the statement.
题意:
有一个圆形迷宫分2层,在12点钟方向有一面墙隔住了第1层和第2层,第1层被n-1面墙平均分为n份,
第2层被m-1面墙平均分为m份,给这些区域按层数和墙分割的部分标上坐标,现在又q个询问,每次询问
给出2个坐标,问这两个坐标对应的部分是否可达
思路:
一开始就想如果要判断可达的情况就要先知道什么时候不可达,不可达就是两层的墙位置重合把路口堵住了,
那么就要知道在什么情况下墙会重合,因为12点钟方向有墙,我们可以把这个圆形迷宫拉伸成两条直线来处理,
观察题目的图发现,1层被分为了4份,2层被分为了6份,4和6的gcd是2,这样就被分为2个2份+3份,每一个2份+3份之内是可达的,
但它们之间是不可达的,因为被墙堵住了,也就是说,求出它们的gcd就知道了能被分为多少份,看2个坐标是不是在同一份中就可知道它们之间是否可达,
当然这只是个猜想,不过试了几个样例之后发现是可以的,于是写了成代码后竟然过了,有时候还是要大胆猜想,灵感很重要
在实现时有一个问题,就是比如题目图片中的样例,(1,1),(1,2),(2,1),(2,2),(2,3)是互相可达的,如果第1层则y/=(n/gcd(n,m)),如果第2层则y/=(m/gcd(n,m))
如果最后两个y相等,则说明他们在同一个可达区域内,但有一个问题,1/2=0,2/2=1,1/3=0,2/3=0,3/3=1,可以发现y%(n/gcd(n,m))==0或y%(m/gcd(n,m))==0的地方除了(n/gcd(n,m))或(m/gcd(n,m))之后多了1,
但他们应该和前面的分为一类,所以当y%(n/gcd(n,m))==0或y%(m/gcd(n,m))==0时我们把他们的y减1,这样就可以和他们前面的分为一类了
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll gcd(ll a,ll b){ 5 return b?gcd(b,a%b):a; 6 } 7 int main(){ 8 ll n,m,q,sx,sy,ex,ey; 9 cin>>n>>m>>q; 10 ll g=gcd(n,m),na=n/g,ma=m/g; ///算gcd和各自要除的数 11 while(q--){ 12 cin>>sx>>sy>>ex>>ey; 13 if(g==1){printf("YES ");continue;} ///如果他们互质则任意坐标都相互可达,因为只有一个连通类 14 if(sx==1){if(sy%na==0)sy--;sy/=na;} ///如果是第一层,如果y是na的倍数,则y要-1,再把y/=na 15 else{if(sy%ma==0)sy--;sy/=ma;} ///否则是第二层,如果y是ma的倍数,则y要-1,再把y/=ma 16 if(ex==1){if(ey%na==0)ey--;ey/=na;} ///与上同理 17 else{if(ey%ma==0)ey--;ey/=ma;} 18 if(sy==ey)printf("YES "); ///如果处理过后的y相等,则说明这两个坐标在同一个连通类内,输出YES 19 else printf("NO "); ///否则输出NO 20 } 21 } 22 /** 23 有一个圆形迷宫分2层,在12点钟方向有一面墙隔住了第1层和第2层,第1层被n-1面墙平均分为n份, 24 第2层被m-1面墙平均分为m份,给这些区域按层数和墙分割的部分标上坐标,现在又q个询问,每次询问 25 给出2个坐标,问这两个坐标对应的部分是否可达 26 一开始就想如果要判断可达的情况就要先知道什么时候不可达,不可达就是两层的墙位置重合把路口堵住了, 27 那么就要知道在什么情况下墙会重合,因为12点钟方向有墙,我们可以把这个圆形迷宫拉伸成两条直线来处理, 28 观察题目的图发现,1层被分为了4份,2层被分为了6份,4和6的gcd是2,这样就被分为2个2份+3份,每一个2份+3份之内是可达的, 29 但它们之间是不可达的,因为被墙堵住了,也就是说,求出它们的gcd就知道了能被分为多少份,看2个坐标是不是在同一份中就可知道它们之间是否可达, 30 当然这只是个猜想,不过试了几个样例之后发现是可以的,于是写了成代码后竟然过了,有时候还是要大胆猜想,灵感很重要 31 在实现时有一个问题,就是比如题目图片中的样例,(1,1),(1,2),(2,1),(2,2),(2,3)是互相可达的,如果第1层则y/=(n/gcd(n,m)),如果第2层则y/=(m/gcd(n,m)) 32 如果最后两个y相等,则说明他们在同一个可达区域内,但有一个问题,1/2=0,2/2=1,1/3=0,2/3=0,3/3=1,可以发现y%(n/gcd(n,m))==0或y%(m/gcd(n,m))==0的地方除了(n/gcd(n,m))或(m/gcd(n,m))之后多了1, 33 但他们应该和前面的分为一类,所以当y%(n/gcd(n,m))==0或y%(m/gcd(n,m))==0时我们把他们的y减1,这样就可以和他们前面的分为一类了 34 **/