jzoj4665. 【GDOI2017模拟7.21】数列

Description

Input

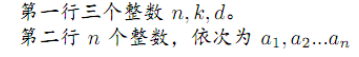
Output

Sample Input

6 1 2
4 3 2 8 6 2

Sample Output

3 5

Data Constraint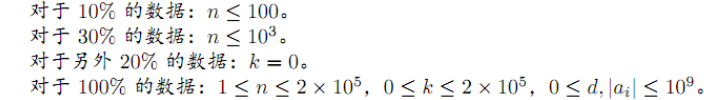

题解

10%
直接暴力$O(n^4)$
然鹅我比赛时竟然没有打出来。
30%
似乎可以$O(n^2 log n)$来搞。
然鹅我不太会。
50%
我更不会。
100%
对于以上的这些，由于数据过于水，所以导致没有几个人能够得到那些部分分。
为什么呢？
因为事实证明，$O(n^2)$竟然是可以水过去的！！！
出题人烂透了。
那么这个$O(n^2)$证明弄呢？
我们发现几个性质：
1、对于可行的答案，都是在一些区间内的。并且这些区间互相之间没有影响。（这个其实没什么用）
2、如果要求答案区间合法，那么区间中每个元素对d取模是一样的。（负数的话直接全部数$+10^9$即可）
3、如果要求答案区间合法，那么必定没有重复的a。
4、如果要求答案区间合法，我们要使得这段区间内满足一个东东：
$frac{max(a)-min(a)}d+1<=r-l+1+k$
什么意思？其中$max(a)$、$min(a)$分别表示答案区间内的最大值与最小值。
满足这个东西就意味着满足了填补k个元素后等差数列是连续的。
至于为什么，自己去翻翻小学奥数。

那么我们现在有上述的4个性质，我们就来暴力了。
首先枚举一个左端点l。然后依次向右边枚举右端点r。
每次r向右边移动一个数字，那么就同时判断一下性质2、3。（2要预处理，3用hash或离散化）
然后如果不满足2、3，则l向右移，r重新枚举。
如果满足，则判断是否满足性质4，满足则更新答案。

其实这个方法很容易卡掉，比如d=1时并且a是递增的，就很容易了。
似乎加个最优性剪枝可以更保险地水过

那么问题来了，如果出题人真的把上面的方法卡掉了，怎么办？

真·100%
我们看到上面的方法，考虑是否可以优化优化。
我们发现，性质2、3很好用，性质4似乎没有用到极致。
而且在暴力过程中l向右移动时，r重新枚举很浪费时间。

那么反过来搞！
考虑先枚举右端点r
我们发现，在满足性质2、3的时候，l是一直递增的。
首先处理出一个数组表示当前第i位满足2、3时最左边可以走到哪里。

然后再考虑性质4。
我们发现，对于确定了一个右端点时，l~r区间内的最大值是递减的。（显然）
同理，l~r区间内的最小值是递增的。
想到什么？单调队列！
每次r往右边移动时，维护一下即可。
对于最大值的单调队列是长这样子的：

我们再返回来看到上面的柿子：
$frac{max(a)-min(a)}d+1<=r-l+1+k$
移项得：
$l+frac{max(a)-min(a)}d<=r+k$
那么我们就可以利用这个限制来找这个l。
在维护单调队列的同时，我们考虑利用线段树来维护某个区间的$frac{max(a)或min(a)}d$即可。
那么每次更新答案就直接在线段树上尽量往左边走就好了。

注意！我们之前求出过一个数组表示当前第i为往左最远达到的位置满足性质2、3.所以我们要判断一下这个边界条件。

标程

$O(n^2)$

uses math;
var
        i,j,k,l,n,m,d,x,y,zd,zx,now,z,jl,ans,op:longint;
        a,b,id,new,mo:array[0..200000] of longint;
        hs:array[1..4000007] of longint;
        flag:array[1..200000] of longint;
        bz:boolean;
procedure qsort(l,r:longint);
var
        i,j,m:longint;
begin
        i:=l;
        j:=r;
        m:=b[(l+r) div 2];
	repeat
                while b[i]<m do inc(i);
                while b[j]>m do dec(j);
		if i<=j then
                begin
                        b[0]:=b[i];b[i]:=b[j];b[j]:=b[0];
                        id[0]:=id[i];id[i]:=id[j];id[j]:=id[0];
			inc(i);
                        dec(j);
		end;
	until i>j;
	if l<j then qsort(l,j);
	if r>i then qsort(i,r);
end;

begin
        //assign(input,'1data.in');reset(input);
        readln(n,k,d);
        for i:=1 to n do
        begin
                read(a[i]);
                a[i]:=a[i]+1000000000;
                mo[i]:=a[i] mod d;
                id[i]:=i;
        end;
        b:=a;
        qsort(1,n);
        j:=0;
        b[0]:=-maxlongint;
        for i:=1 to n do
        begin
                if b[i]<>b[i-1] then
                begin
                        inc(j);
                end;
                new[id[i]]:=j;
        end;
        for i:=1 to n do
        begin
                op:=-1;
                zd:=-maxlongint;
                zx:=maxlongint;
                for j:=i to n do
                begin
                        x:=new[j];
                        if flag[x]=i then
                        begin
                                break;
                        end
                        else
                        begin
                                flag[x]:=i;
                                if op<0 then
                                begin
                                        op:=mo[j];
                                end
                                else
                                begin
                                        if mo[j]<>op then
                                        begin
                                                break;
                                        end;
                                end;
                                zd:=max(zd,a[j]);
                                zx:=min(zx,a[j]);
                                if (zd-zx) div d+1<=k+(j-i+1) then
                                begin
                                        if (j-i+1)>ans then
                                        begin
                                                ans:=j-i+1;
                                                now:=i;
                                        end;
                                end;
                        end;
                end;
        end;
        writeln(now,' ',now+ans-1);
end.

$O(n log n)$

uses math;
var
        i,j,k,l,n,m,d,x,y,zd,zx,now,z,jl,ans,op,head,tail,last:longint;
        a,b,id,new,mo,zz,mx,mn,p,q:array[0..200000] of longint;
        flag:array[1..200000] of boolean;
        tree,lazy:array[1..800000]of int64;
        bz:boolean;
procedure qsort(l,r:longint);
var
        i,j,m:longint;
begin
        i:=l;
        j:=r;
        m:=b[(l+r) div 2];
	repeat
                while b[i]<m do inc(i);
                while b[j]>m do dec(j);
		if i<=j then
                begin
                        b[0]:=b[i];b[i]:=b[j];b[j]:=b[0];
                        id[0]:=id[i];id[i]:=id[j];id[j]:=id[0];
			inc(i);
                        dec(j);
		end;
	until i>j;
	if l<j then qsort(l,j);
	if r>i then qsort(i,r);
end;
procedure make_tree(x,l,r:longint);
var
        m:longint;
begin
        if l=r then tree[x]:=l
        else
        begin
                m:=(l+r) shr 1;
                make_tree(x*2,l,m);
                make_tree(x*2+1,m+1,r);
                tree[x]:=min(tree[x+x],tree[2*x+1]);
         end;
end;
procedure change(x,l,r,st,en,value:longint);
var
        m:longint;
begin
        if (l=st)and(r=en) then
        begin
                inc(tree[x],value);
                inc(lazy[x],value);
        end
        else
        begin
                inc(tree[2*x],lazy[x]);
                inc(tree[2*x+1],lazy[x]);
                inc(lazy[2*x],lazy[x]);
                inc(lazy[2*x+1],lazy[x]);
                lazy[x]:=0;
                m:=(l+r)shr 1;
                if en<=m then change(2*x,l,m,st,en,value)
                else if st>m then change(2*x+1,m+1,r,st,en,value)
                else
                begin
                        change(2*x,l,m,st,m,value);
                        change(2*x+1,m+1,r,m+1,en,value);
                end;
                tree[x]:=min(tree[2*x],tree[2*x+1]);
        end;
end;
procedure find(x,l,r,yb:longint);
var
        m:longint;
begin
        if (l=r) then
        begin
                ans:=l;
        end
        else
        begin
                inc(tree[2*x],lazy[x]);
                inc(tree[2*x+1],lazy[x]);
                inc(lazy[2*x],lazy[x]);
                inc(lazy[2*x+1],lazy[x]);
                lazy[x]:=0;
                m:=(l+r)shr 1;
                if tree[2*x]<=yb then find(2*x,l,m,yb)
                else find(2*x+1,m+1,r,yb);
        end;
end;

begin
        assign(input,'1data.in');reset(input);
        readln(n,k,d);
        for i:=1 to n do
        begin
                read(a[i]);
                a[i]:=a[i]+1000000000;
                mo[i]:=a[i] mod d;
                id[i]:=i;
        end;
        b:=a;
        qsort(1,n);
        j:=0;
        b[0]:=-maxlongint;
        for i:=1 to n do
        begin
                if b[i]<>b[i-1] then
                begin
                        inc(j);
                end;
                new[id[i]]:=j;
        end;
        l:=1;
        flag[new[1]]:=true;
        zz[1]:=1;
        op:=mo[1];
        for i:=2 to n do
        begin
                if i=5 then
                j:=j;
                while (l<i) and (flag[new[i]]) do
                begin
                        flag[new[l]]:=false;
                        inc(l);
                        op:=mo[l];
                end;
                while (l<i) and (op<>mo[i]) do
                begin
                        flag[new[l]]:=false;
                        inc(l);
                        op:=mo[l];
                end;
                flag[new[i]]:=true;
                zz[i]:=l;
        end;
        make_tree(1,1,n);
        head:=1;tail:=1;
        mx[1]:=1;mn[1]:=1;p[1]:=1;q[1]:=1;
        for i:=2 to n do
        begin
                last:=i-1;
                while (head>0) and (a[mx[head]]<=a[i]) do
                begin
                        change(1,1,n,p[head],last,(a[i]-a[mx[head]]) div d);
                        last:=p[head]-1;
                        dec(head);
                end;
                inc(head);mx[head]:=i;p[head]:=last+1;
                last:=i-1;
                while (tail>0) and (a[mn[tail]]>=a[i]) do
                begin
                        change(1,1,n,q[tail],last,(a[mn[tail]]-a[i]) div d);
                        last:=q[tail]-1;
                        dec(tail);
                end;
                inc(tail);mn[tail]:=i;q[tail]:=last+1;
                if zz[i]>1 then
                change(1,1,n,1,zz[i]-1,maxlongint div 3);
                ans:=0;
                find(1,1,n,i+k);
                if i-ans+1>zd then
                begin
                        zd:=i-ans+1;
                        now:=ans;
                end;
        end;
        writeln(now,' ',now+zd-1);
end.
end.

虽说长了点，但是时间却异常优秀。对比一下就知道了。
上面是$O(n log n)$
下面是$O(n^2)$