学习burnside、polya小结

前言

我好蔡啊
之前597问我群论是什么，我一脸懵逼。
心中暗自安慰自己——这玩意对现在的我用处不大。
没想到第二天比赛就出了这么一道题。
由于临近中考，中考压力过大，没有细学。
硬着头皮，好歹也算是学会了。

简介

群论是法国数学家伽罗瓦（Galois）的发明。伽罗瓦是一个极具传奇性的人物，年仅21岁就英年早逝于一场近乎自杀的决斗中。他用该理论，具体来说是伽罗瓦群，解决了五次方程问题。在此之前柯西（Augustin-Louis Cauchy)，阿贝尔（Niels Henrik Abel）等人也对群论作出了贡献。
——来自百度百科

管他什么自杀的决斗呢，如果想知道为什么，去看看历史说不定知道。
这不是重点。

群论有很多很多的分支，但其中信息学主要利用的是其中的burnside与polya。

群的定义

首先，这个不重要。（其实是我懒得打一些奇奇怪怪的符号）
贴一下百度百科的，了解一下即可

置换

首先，置换这个玩意儿有点难以理解。

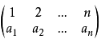
上面一排表示1被1到n中某个数$a_1$取代，2被1到n中某个数$a_2$代替，……，一直到n。
并且$a_1,a_2,a_3,……,a_n$互不相同。

置换群

其实这个就是一个置换的连接。
它也满足群的4个条件：

百度百科写的真好。

Burnside引理

Burnside引理是一个结论，用来计算组合数中的等价类计算。是用于Polya的
用$D(a_j)$表示在置换$a_j$下不变的元素的个数，也可称作不定点。
用L表示本质不同的方案数。

结论就是：
$L=frac{1}{|G|}sum_{j=1}^sD(a_j)$
证明看这里 https://baike.baidu.com/item/burnside引理/1505996?fr=aladdin

我们用一道题目来理解这个玩意：
SGU294 He’s Circles
大意就是给你一个有n颗珠子的项链，上面写着“X”和“E”，问本质不同的环有多少种。
（本质不同的环指循环重构后相同，例如XEX与XXE是同一种情况）

从这个题下手，当N=4时，一共有4种置换：（用s表示）

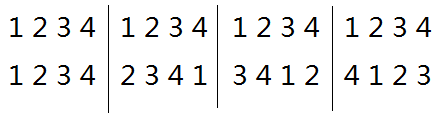
我们发现，所有的方案在置换$a_1$下都不变，则$D(a_1)=16$
XXXX、EEEE在置换$a_2$下不变，则$D(a_2)=2$
XXXX、EEEE、XEXE、EXEX在置换$a_3$下不变，则$D(a_3)=4$
XXXX、EEEE在置换$a_4$下不变，则$D(a_4)=2$
根据引理计算，可以得到：$L=6$

这个玩意儿很好用，可是其中的D很不好求，怎么办呢？

Polya定理

如果我们利用爆搜来搞其中的D，可以发现时间复杂度及其的BIG。
接下来就要运用到polya定理了。

首先，我们要明白循环节是什么东东。
$（a1a2……an）=(^{a1a2……an}_{a2a3……a1})$
举个例子：

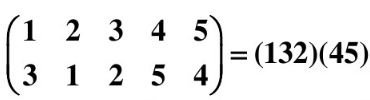
我们发现，其中（132）就是前面3个数字旋转。（45）这是后面2个数字旋转。
由此可知，每个置换都可以写成若干个互不相交的循环。
如上面（132）与（45）就互不相交。
那么，循环节则表示一个置换中的循环个数。上述的循环节个数为2.

实在无法理解可以看看这个：
https://wenku.baidu.com/view/8ae2981033d4b14e84246829.html

正题：
Polya定理：设G为一个置换群，如上面一题，用m种颜料涂染n个珠子，则方案为：
$L=frac1{|G|}(m^{c(g_1)}+m^{c(g_2)}+……+m^{c(g_s)})$
其中：$c(g_i)$表示$g_i$置换的循环节数，$G=(g_1,g_2,……,g_s)$

继续举个例子：
同上题：
$g_1$为（2,3,4,1）则$g_1=(4321),c(g_1)=1$
$g_2$为（3,4,1,2）则$g_2=(13)(24),c(g_2)=2$
$g_3$为（4,1,2,3）则$g_3=(1234),c(g_3)=1$
$g_4$为（1,2,3,4）则$g_4=(1)(2)(3)(4),c(g_4)=4$
因为$m=2$则算出来可得$L=6$

接下来分析时间复杂度：
通常情况下：
求出一个置换的循环节点数：$O(n)$
求出每个置换：$O(s)$
结合起来就是：$O(sn)$
非常优秀。

在上面的这道题，我们发现，$c(g_i)=n/gcd(n,i)$
感性理解理解。
所以就更加优秀了。

例题

jzoj4800. 【GDOI2017模拟9.24】周末晚会

参考资料

本人版权意识薄
https://blog.csdn.net/liangzhaoyang1/article/details/72639208
https://wenku.baidu.com/view/8ae2981033d4b14e84246829.html
https://blog.csdn.net/gmh77/article/details/90731621
百度百科