Description
自从 Y 君退役之后,她就迷上了吃鸡,于是她决定出一道吃鸡的题。
Y 君将地图上的所有地点标号为 1 到 n,地图中有 n − 1 条双向道路连接这些点,通过一条 双向道路需要一定时间,保证从任意一个点可以通过道路到达地图上的所有点。
有些点上可能有资源,Y 君到达一个有资源的点后,可以选择获取资源来使自己的武力值增 加 wi,也可以选择不获取资源。如果 Y 君获取了一个点上的资源,这个点上的资源就会消失,获 取资源不需要时间。
有些点上可能有敌人,Y 君到达一个有敌人的点后,必须花费 ti 秒伏地与敌人周旋,并最终 将敌人消灭。如果 Y 君消灭了一个点上的敌人,这个点上的敌人就会消失。Y 君不能无视敌人继 续前进,因为这样会被敌人攻击。
如果一个点上既有资源又有敌人,Y 君必须先消灭敌人之后才能获取资源,否则就会被敌人 突袭。
游戏开始时,Y 君可以空降到任意一个点上,接下来,她有 T 秒进行行动,T 秒后她就必须 前往中心区域送快递。Y 君希望她前往中心区域送快递时,武力值尽可能大,请你帮助 Y 君设计 路线,以满足她的要求。你只需输出 T 秒后 Y 君的武力值。
Input
第一行由单个空格隔开的两个正整数 n, T,代表点数和时间。
第二行 n 个由单个空格隔开的非负整数代表 wi,如果 wi = 0 代表该点没有武器,
第三行 n 个由单个空格隔开的非负整数代表 ti,如果 ti = 0 代表该点没有敌人。
接下来 n − 1 行每行由单个空格隔开的 3 个非负整数 a, b, c 代表连接 a 和 b 的双向道路,通 过这条道路需要 c 秒。
Output
输出一行一个整数代表 T 秒后 Y 君的武力值。
Sample Input
17 54
5 5 1 1 1 25 1 10 15 3 6 6 66 4 4 4 4
0 1 3 0 0 0 1 3 2 0 6 7 54 0 0 0 0
1 8 3
2 8 3
8 7 7
7 13 0
7 14 0
15 14 2
16 14 3
17 14 5
7 9 4
9 10 25
10 11 0
10 12 0
7 6 20
3 6 3
3 4 3
3 5 3
Sample Output
68
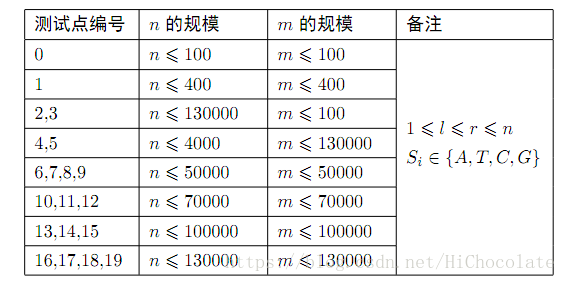
Data Constraint
题解:
10%输出0
20%不会。
40%可以直接做一遍背包。
60%不知道。
还是直接上100%把。
首先,我们这题显然是一道树形DP题。
我们可以设三个状态转移方程——
f[i,j]进入以i为根的子树并返回到i
g[i,j]进入以i为根的子树但不返回到i
h[i,j]从以i为根的子树里一点出发,经过i点并调回以i为根的子树中
用了j秒的最大武力值。
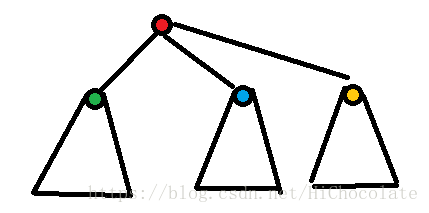
这是一张通用的图。
于是乎,我们可以对于每一个方程来讨论。
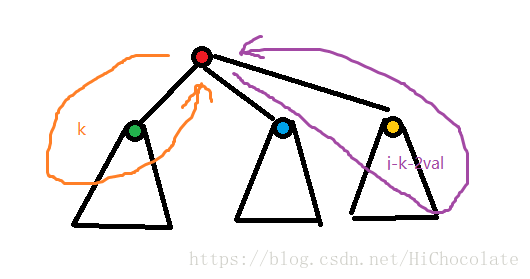
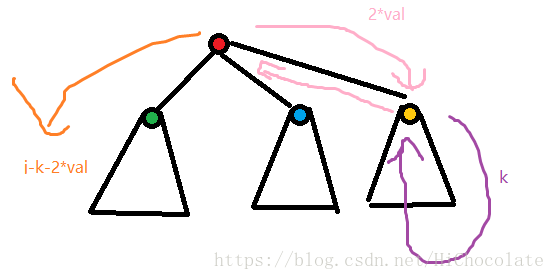
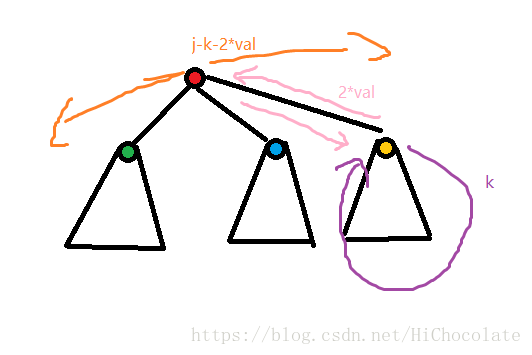
对于f[i,j]:f[i,j]:=max(f[i,j],f[i,j-k-2val]+f[son,k]);
表达的意思是:先从i(红色)走到儿子节点,有k的时间在i的儿子节点走,走到后返回son,然后返回i,然后i再走j-k-2val的时间返回到i。
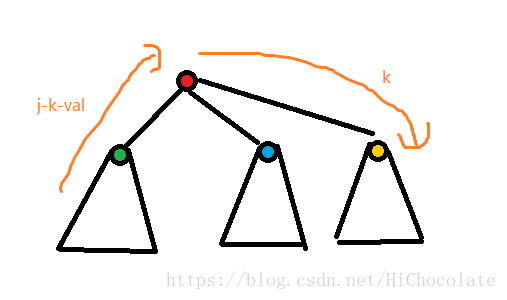
对于g[i,j]:
g[i,j]:=max(g[i,j],g[son,k]+f[i,j-k-val]);
表达的意思是:在i这个节点先乱走一通,回到i点,然后再走到son的节点,给这个节点k的时间走,走完之后不回来了。
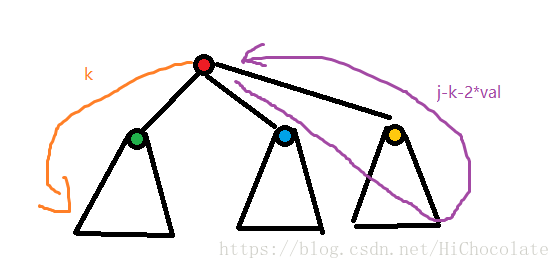
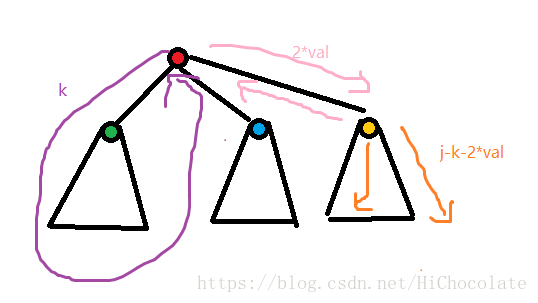
g[v,j]:=max(g[i,j],g[i,j-k-2*val]+f[son,k]);
表达的意思是:在i这个节点上,走到一个儿子,然后乱走回到这个儿子,返回i点,最后再走完后不回来了。
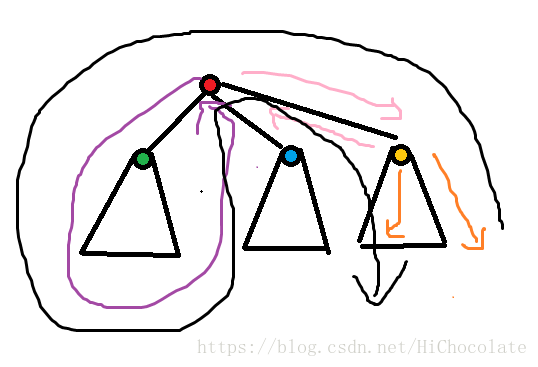
对于h[i,j]
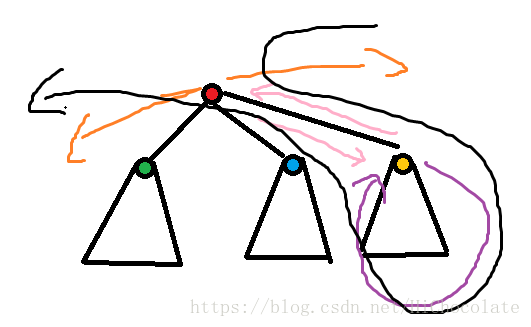
h[i,j]:=max(h[i,j],g[i,j-k-val]+g[son,k]);
表达的意思是:首先,从i乱走,然后,i的儿子乱走,两段连起来就相当于从i子树中一个点走到i,走到i的一个儿子,再走到终点。
h[i,j]:=max(h[i,j],f[i,k]+h[son,j-k-2*val]);
表达的意思是:首先,i的儿子的h找到,再从i乱走一通,回到i点。拆开来看就相当于son的子树中一点走到son再走到i再乱走返回i再回到son再乱走。
相当于:
h[i,j]:=max(h[i,j],f[son,k]+h[i,j-k-2*val]);
表达的意思是:首先,i的h找到,再从son乱走一通,回到son点。拆开来看就相当于i的子树中一点走到i再走到son再乱走返回son再回到i再乱走。
相当于:
然后,就可以很舒服地DP啦。
只是要注意一些DP顺序,否则会导致算重,还有就是边界条件(卡了我好久)
标程
uses math;
var
i,j,k,l,n,m,time,tot,ans:longint;
x,y,z,tov,next,last,val:array[1..10000] of longint;
f,g,h:array[1..300,0..300] of longint;
w,t:array[1..300] of longint;
procedure insert(x,y,z:longint);
begin
inc(tot);
tov[tot]:=y;
next[tot]:=last[x];
last[x]:=tot;
val[tot]:=z;
end;
procedure dfsf(v,fa:longint);
var
i,j,k:longint;
yz:boolean;
begin
if t[v]>time then exit;
i:=last[v];
yz:=false;
while i>0 do
begin
if tov[i]<>fa then
begin
yz:=true;
dfsf(tov[i],v);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=2*val[i] then
h[v,j]:=max(h[v,j],f[tov[i],k]+h[v,j-k-2*val[i]]);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=2*val[i] then
h[v,j]:=max(h[v,j],f[v,k]+h[tov[i],j-k-2*val[i]]);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=val[i] then
h[v,j]:=max(h[v,j],g[v,j-k-val[i]]+g[tov[i],k]);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=2*val[i] then
g[v,j]:=max(g[v,j],g[v,j-k-2*val[i]]+f[tov[i],k]);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=val[i] then
g[v,j]:=max(g[v,j],g[tov[i],k]+f[v,j-k-val[i]]);
for j:=time downto 0 do
for k:=0 to j do
if j-k>=2*val[i] then
f[v,j]:=max(f[v,j],f[v,j-k-2*val[i]]+f[tov[i],k]);
end;
i:=next[i];
end;
// f[v,t[v]]:=w[v];
begin
for i:=time downto t[v] do
begin
f[v,i]:=f[v,i-t[v]]+w[v];
g[v,i]:=g[v,i-t[v]]+w[v];
h[v,i]:=h[v,i-t[v]]+w[v];
end;
for i:=min(t[v]-1,time) downto 0 do
begin
f[v,i]:=0;
g[v,i]:=0;
h[v,i]:=0;
end;
end;
end;
begin
assign(input,'toyuq.in');reset(input);
assign(output,'toyuq.out');rewrite(output);
readln(n,time);
for i:=1 to n do
begin
read(w[i]);
ans:=max(w[i],ans);
end;
if ans=0 then
begin
writeln(0);
halt;
end;
readln;
for i:=1 to n do read(t[i]);
for i:=1 to n-1 do
begin
readln(x[i],y[i],z[i]);
insert(x[i],y[i],z[i]);
insert(y[i],x[i],z[i]);
end;
dfsf(1,0);
ans:=0;
for i:=1 to n do
begin
ans:=max(ans,h[i,time]);
end;
writeln(ans);
end.