#Description
暑假里,总有某些同学由于贪玩而忘记做作业。这些人往往要等到暑假快结束时才想起堆积如山的作业,但在这最后几天的时间里把这些作业做完已经不太现实了,于是“志同道合”的他们想出了一个妙招。
假设现在有n科作业,他们把第i科作业按作业量平均分成ai份,他们总共有m个人,第j个人只愿意做其中任意的bj份作业,而且我们知道ai的和等于bj的和,以及把第i科作业的其中一份给第j个人做的时间是ci,j。现在他们想分配下各自的任务,一起把作业做完,然后再%#&%&#%%&^
现在的问题来了,他们希望所有人做作业的总时间的和最小,你能帮助他们解决问题吗?
#Input
输入文件的第一行有两个n,m表示有多少科作业和多少个人,第二行有n个数依次表示ai,第三行有m个数依次表示bj,最后n行,每行m个数表示ci,j。
#Output
输出文件包含一行为最少的时间总和。
#Sample Input
2 2
3 5
5 3
1 2
2 1
#Sample Output
10
【样例解释】
第1个人做完所有的第1科作业以及第2科作业的其中2份,第2个人把第2科另外3份做完。
#Data Constraint
第一个点 n<=5 m<=5 ai,bi<=15 sum(ai)<=20
第二个点 n<=10 m<=10 ai,bi<=20 sum(ai)<=100
第三个点 n<=30 m<=30 ai,bi<=600 sum(ai)<=10000
第四个点到第十个点 n<=200 m<=200 ai,bi<=10000 sum(ai)<=1000000
#题解
题意:很好懂。
然后第一眼(很关键):最小费用最大流。
很暴力,但是看到数据感觉很正确。
恩,然后就暴力码3小时。0分。
为什么呢?因为我打错了一些东东,小数据竟然没有拍出来!
然后TLE40。
为什么呢?因为最小费用最大流的时间复杂度很玄学,而且时间限制为500ms。管他是什么zkw或是最普通的spfa,我出题人绝对卡掉。
100%
题解直接否决了最小费用最大流。然后就讲到拆点做一边二分图匹配。
然而点数很大,然后就用一种我不懂的方法来拆点,然后做KM(带权二分图匹配)。
然后题解我丢在这里大家慢慢看。
那我怎么做的呢?
真·100%
其实有另一种方法是可以用费用流来做的。垃圾出题人
我们建图就:
1)源点连流量为y[i],费用为0的点到每个人
2)中间每个人连流量为INF,费用为w[i,j]的到每个作业。
3)每个作业连流量为x[i],费用为0的点到汇点。
然后呢,这样直接做是会爆的。
那么我们就考虑考虑优化。
我们发现,对于zkw或是别的费用流,都是根据一个最短路(费用为路的长度),然后来更新流量。
这个跟EK的算法很相似,自己学,我不讲,难不成你咬我?
然后呢,我们发现,每次更新,我们只会流最短的路,于是我们就可以动态地来加入一些点,不用每次都循环这么多次。
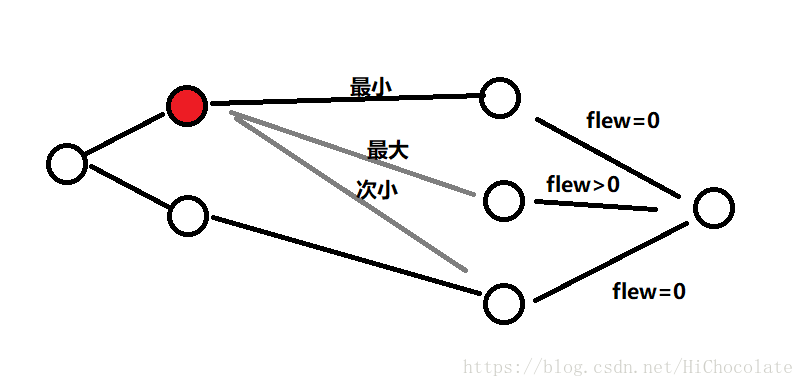
至于如何弄,我们来看一张图:
这张图上,我们流完了第一次,要加入灰色的边。那么我们由于加入了最小的边,然后最小的边连到的点的flew=0,那么我们就找到次小,加入。由于次小的边连到的点的flew也为0,那么我们继续找。找到一条边——最大,它的连到的点的flew>0于是乎,我们就可以停止当前点的加边。
这样子我们在每次更新流量时,不会跑过多的边导致时间保证不了。
神奇的优化。
然后如果你打得丑像我一样,你可能需要用到一些O3常数上的优化。
我P党真的无语,这个方法跑600、700ms,别的C党就100ms200ms。
但是事后我转成C了之后一样是卡过去的,而且代码量惊人。
#include<bits/stdc++.h>
using namespace std;
bool b[100002],pd[100002];
int i,j,k,l,n,m,t,tot,tot1,js,w[301][301],mapp[301][301],op[301][301],x[100001],y[100001];
long long ans,maxx,last[100001],next[100001],tov[100001],last1[100001],flew1[100001],next1[100001],tov1[100001],flew[100001],value[100001],value1[100001],id1[100001],id[100001],bh[100001],kp[100001],dis[100001],d[100001],now[100001],need[100001];
__attribute__((optimize("O3")))
void ort(int l,int r,int p)
{
int i=l,j=r,k,m;
m=mapp[l+(r-l)/3][p];
do
{
while(mapp[i][p]<m)i++;
while(mapp[j][p]>m)j--;
if(i<=j)swap(mapp[i][p],mapp[j][p]),swap(op[i][p],op[j][p]),i++,j--;
}while(i<=j);
if(l<j)ort(l,j,p);
if(r>i)ort(i,r,p);
}
__attribute__((optimize("O3")))
void insert2(int x,int y){tot1++,tov1[tot1]=y,next1[tot1]=kp[x],kp[x]=tot1;}
__attribute__((optimize("O3")))
void insert1(int x,int y){tot1++,tov1[tot1]=y,next1[tot1]=last1[x],last1[x]=tot1;}
__attribute__((optimize("O3")))
void insert(int x,int y){tot++,tov[tot]=y,next[tot]=last[x],last[x]=tot;}
__attribute__((optimize("O3")))
long long min(int x,long long y){if(x<y)return x;return y;}
__attribute__((optimize("O3")))
int flow(int x,int t)
{
int k,l;
long long minn;
pd[x]=true;
if(x==n+m+2){ans+=t*dis[1];return t;}
k=last1[x];
while(k!=0)
{
if((flew1[k]>0)and (pd[tov1[k]]==false) and (dis[x]==dis[tov1[k]]+value1[k]))
{
minn=min(t,flew1[k]);
l=flow(tov1[k],minn);
if(l>0)
{
flew1[id1[k]]+=l;
flew1[k]-=l;
last1[x]=k;
return l;
}
}
k=next1[k];
}
last1[x]=0;
return 0;
}
__attribute__((optimize("O3")))
bool change()
{
int minn=2147483647,k;
for(i=1;i<=n+m+2;i++)
{
if(pd[i])
{
k=kp[i];
while(k!=0)
{
if((flew1[k]>0)and(pd[tov1[k]]==false)and(dis[tov1[k]]+value1[k]-dis[i]<minn))
minn=dis[tov1[k]]+value1[k]-dis[i];
k=next1[k];
}
}
}
if(minn==2147483647)return true;
for(i=1;i<=n+m+2;i++)
if(pd[i])dis[i]+=minn,pd[i]=false;
return false;
}
__attribute__((optimize("O3")))
void up(int x){while((x/2>0)and(dis[d[x]]<dis[d[x/2]]))bh[d[x]]=x/2,bh[d[x/2]]=x,swap(d[x],d[x/2]),x/=2;}
__attribute__((optimize("O3")))
void down(int y)
{
int x=1;
while(((x*2<=t)and (dis[d[x]]>dis[d[x*2]])) or ((x*2+1<=t) and (dis[d[x]]>dis[d[x*2+1]])))
{
if ((x*2+1<=t) and (dis[d[x*2+1]]<dis[d[x*2]]))
bh[d[x]]=x*2+1,bh[d[x*2+1]]=x,swap(d[x],d[x*2+1]),x=x*2+1;
else
bh[d[x]]=x*2,bh[d[x*2]]=x,swap(d[x],d[x*2]),x*=2;
}
}
__attribute__((optimize("O3")))
inline char nc(){ static char buf[100000],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++; }
__attribute__((optimize("O3")))
void read(int &data){data=0;char ch=0; while(ch<'0'||ch>'9')ch=nc(); while(ch>='0'&&ch<='9')data=data*10+ch-'0',ch=nc();}
__attribute__((optimize("O3")))
int main()
{
read(n),read(m);
for(i=1;i<=n;i++)read(y[i]);
for(i=1;i<=m;i++)read(x[i]);
for(i=1;i<=n;i++)for(j=1;j<=m;j++)read(w[i][j]),mapp[i][j]=w[i][j];
for(i=1;i<=m;i++)for(j=1;j<=n;j++)op[j][i]=j+m+1;
for(i=1;i<=m;i++)insert(1,1+i),flew[tot]=x[i],insert(1+i,1),flew[tot]=x[i];
for(i=1;i<=n;i++)for(j=1;j<=m;j++)insert(j+1,i+m+1),value[tot]=w[i][j],flew[tot]=2147483647,insert(i+m+1,j+1),flew[tot]=2147483647,value[tot]=w[i][j];
for(i=1;i<=n;i++)insert(1+m+i,2+n+m),flew[tot]=y[i],insert(2+n+m,1+m+i),flew[tot]=y[i];
for(i=0;i<=100000;i++)dis[i]=2147483647;
maxx=dis[1],t=1,dis[n+m+2]=0,b[n+m+2]=true,bh[n+m+2]=t,d[t]=n+m+2;
up(t);
while (t>0)
{
b[d[1]]=true,i=last[d[1]];
while(i>0)
{
if((b[tov[i]]==false)and(dis[d[1]]+value[i]<dis[tov[i]]))
{
if(dis[tov[i]]==maxx)
t++,dis[tov[i]]=dis[d[1]]+value[i],bh[tov[i]]=t,d[t]=tov[i],up(t);
else
dis[tov[i]]=dis[d[1]]+value[i],up(bh[tov[i]]);
}
i=next[i];
}
bh[d[1]]=0,bh[d[t]]=1,d[1]=d[t],t--,down(t);
}
for(i=1;i<=m;i++)insert1(1,1+i),value1[tot1]=0,id1[tot1]=tot1+1,flew1[tot1]=x[i],insert1(1+i,1),id1[tot1]=tot1-1,flew1[tot1]=0,value1[tot1]=0;
for(i=1;i<=n;i++)insert1(1+m+i,2+n+m),need[i+m+1]=tot1,value1[tot1]=0,id1[tot1]=tot1+1,flew1[tot1]=y[i],insert1(2+n+m,1+m+i),id1[tot1]=tot1-1,flew1[tot1]=0,value1[tot1]=0;
for(i=1;i<=m;i++)now[i]=1;
for(i=1;i<=m;i++)ort(1,n,i),insert1(i+1,op[now[i]][i]),value1[tot1]=mapp[1][i],id1[tot1]=tot1+1,flew1[tot1]=2147483647,insert1(op[now[i]][i],i+1),value1[tot1]=-mapp[1][i],id1[tot1]=tot1-1,flew1[tot1]=0;
for(i=0;i<=100000;i++)kp[i]=last1[i];
do
{
for(i=1;i<=n+m+2;i++)last1[i]=kp[i];
while(flow(1,2147483647)>0)
for(i=1;i<=n+m+2;i++)pd[i]=false;
for(i=1;i<=m;i++)
{
if(now[i]==n)continue;
j=kp[i+1];
while(j>0)
{
if(tov1[j]!=1)
{
k=need[tov1[j]];
if(flew1[k]==0)
{
now[i]++;
if(now[i]>n)break;
insert2(i+1,op[now[i]][i]);
value1[tot1]=mapp[now[i]][i];
id1[tot1]=tot1+1;
flew1[tot1]=2147483647;
insert2(op[now[i]][i],i+1);
value1[tot1]=-mapp[now[i]][i];
id1[tot1]=tot1-1;
flew1[tot1]=0;
}
}
j=next1[j];
}
}
}while(!change());
printf("%lld",ans);
}