士兵
题目描述
在Gridland国家,有N个处于不同位置的士兵。该国上的地方都用两个坐标(X,Y)来表示。士兵能进行一次移动,每个士兵都可向上、向下、向左、或向右移动一个单位长,这样他就能把自己的X或Y改变1或-1。
士兵们想进入一个水平线,彼此靠近,这样他们的最后位置就是(X,Y)、(X+1,Y),…,(X+N,Y))。水平线上的士兵的最后顺序以及整数X和Y,都是任意的。
现在目标是求如此配置士兵的最少移动数。
两个或两个以上的士兵在同一时间不处于同一位置。
输入
输入文件soldiers.in的第一行含有一个整数N,1 <= N <=10000,N为士兵的数量。输入文件以后的N行应含有士兵的初始位置,对于每一个i, 1<= i <= N,输入文件的第I+1行含有两个用空格分开的整数x[i],y[i],他们表示第I个士兵的坐标,-10000<=x[i],y[i] <=10000.
输出
输出文件soldiers.out仅有一行,它的值为使士兵移动到水平线彼此相邻的最小移动次数。
样例输入
5
1 2
2 2
1 3
3 -2
3 3
样例输出
8
题解:
此题就是一个恶心的数学规律题。
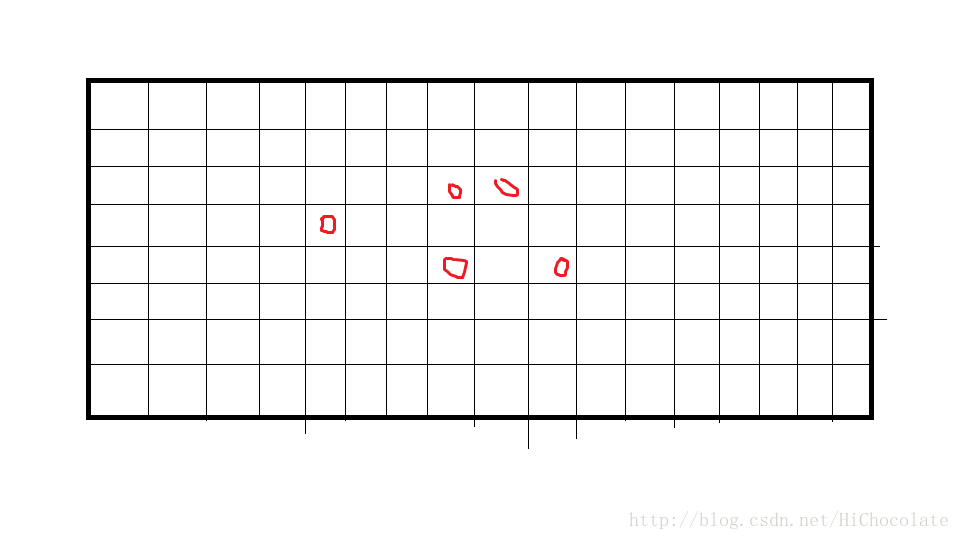
题意说:士兵们想进入一个水平线,彼此靠近,这样他们的最后位置就是(X,Y)、(X+1,Y),…,(X+N,Y))。那么我们就会发现,士兵们合在一条水平线的位置,就是水平线的中间那条线。如图:
红色表示士兵。
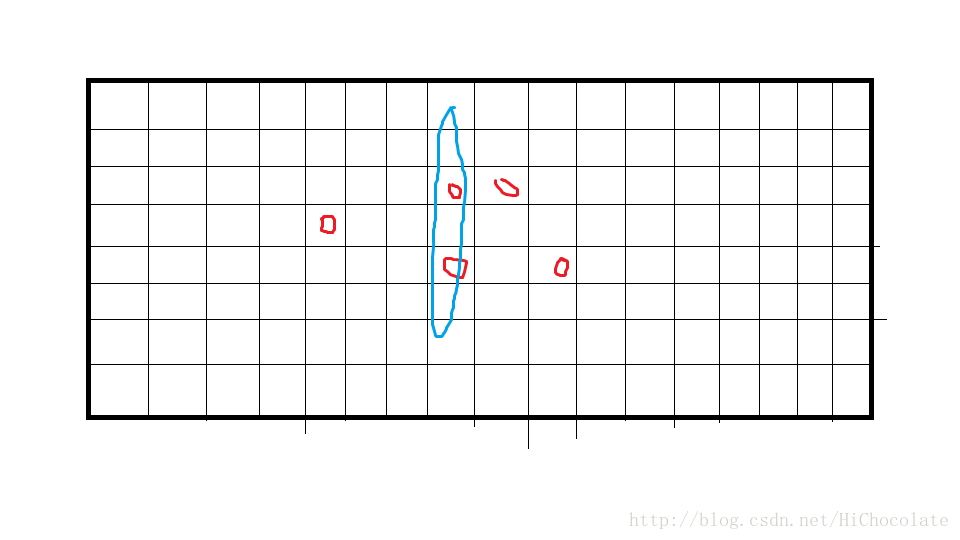
中间的集合线是:
蓝色标记的线最优。
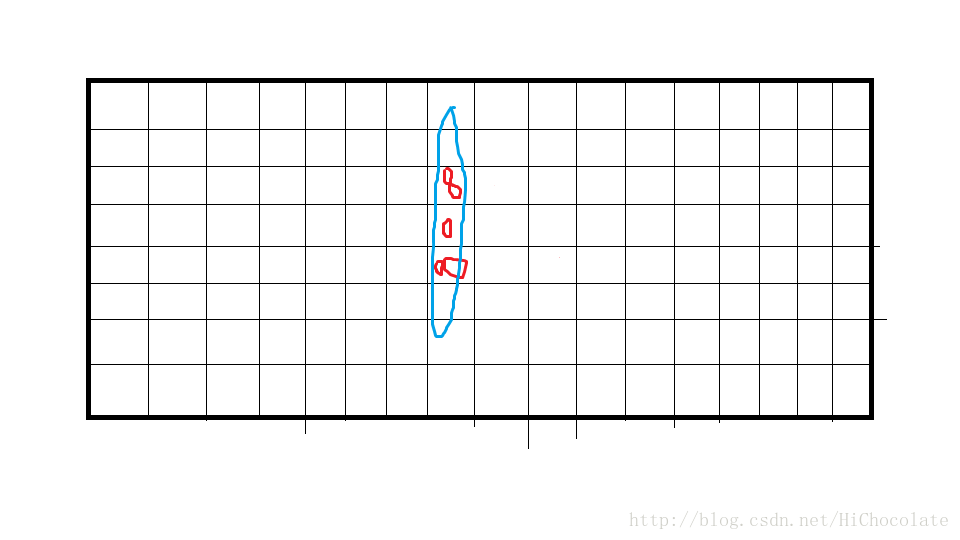
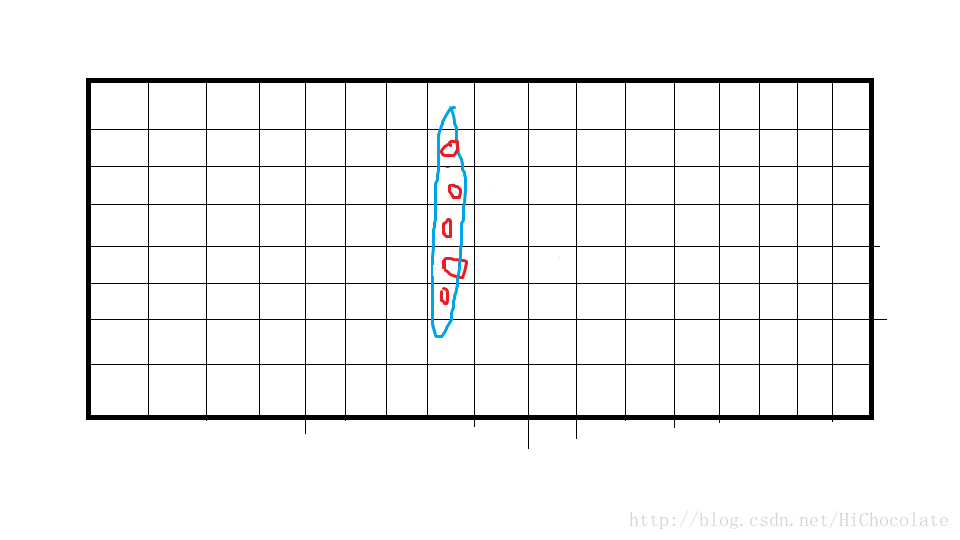
于是乎,我们就把所有士兵给直接集合到此直线(不管重合),得到:
图中两个红圈表示有两个士兵。
他们集合到一条直线所需次数:6.
现在,用一个x来表示每个红圈的x坐标,再排序。如图例得:
1 1 2 3 3
再因为士兵要紧密相连,所以最终队列应为:
答案为6+2=8.
如何处理这一段???
我们就来看:x
1 1 2 3 3
排好队最终的序号为:
1 2 3 4 5
再由想x[i]-i+1得:
1 0 0 0 -1
快排。
-1 0 0 0 1
从中间拓展,
于是搞搞就OK了。
标程:
type
new=array[1..10000] of longint;
var
a:array[1..10000] of longint;
b,z:array[-10000..10000] of longint;
x,y,x1,y1:array[1..10000] of longint;
i,j,k,l,n,m,sum,mid:longint;
procedure qs(l,r:longint;var a:new);
var
i,j,m,t:longint;
begin
i:=l;
j:=r;
m:=a[(l+r)div 2];
repeat
while a[i]<m do inc(i);
while a[j]>m do dec(j);
if i<=j then
begin
t:=a[i];
a[i]:=a[j];
a[j]:=t;
inc(i);
dec(j);
end;
until i>j;
if l<j then qs(l,j,a);
if i<r then qs(i,r,a);
end;
begin
assign(input,'soldiers.in');reset(input);
assign(output,'soldiers.out');rewrite(output);
readln(n);
for i:=1 to n do
begin
readln(x[i],y[i]);
end;
if n mod 2=1 then
mid:=(n+1) div 2
else
mid:=n div 2;
qs(1,n,y);
for i:=1 to n do
begin
sum:=sum+abs(y[i]-y[mid]);
end;
qs(1,n,x);
for i:=1 to n do
begin
x[i]:=x[i]-i+1;
end;
qs(1,n,x);
for i:=1 to n do
begin
sum:=sum+abs(x[i]-x[mid]);
end;
writeln(sum);
close(input);close(output);
end.