**【2011.12.10普及模拟】泽泽在埃及 **
题目描述
泽泽已52:0的比分输了球,被足球流氓打了一顿,扔进了窨井里……
出来的时候,泽泽已经在埃及了。
滚滚的黄沙在周围飞舞,没有一样生物在这里栖息。泽泽不想就挂在这里。忽然,泽泽被风沙遮住的眼睛瞥见了一座金字塔。这是一座很雄伟的金字塔,而且重要的是,金字塔顶端,竟然有一架直升飞机!
泽泽就像抓到了救命稻草,用他在长城上999999999999999999 mod 2倍的速度疯狂向金字塔奔跑。来到金字塔下,风把他刮进了金字塔。
门“轰隆隆”地关上了。泽泽看见里面陈列着很多珍品,但依然存在着暗器。但是还好,有个盗墓的把木乃伊给挖走了,所以在金字塔里没有跳动的僵尸。泽泽需要做的就是尽快跑向金字塔的顶端。
现在泽泽在金字塔最底层的左上角。他可以向前后左右或走到楼上去,但必须花费一点时间。一旦走到楼上后楼下的门就会关闭,泽泽不能回下去了,因此泽泽格外小心。幸运的是,金字塔很巧妙。在金字塔里有一些暗道,可以从某点直接通向某点,而不用再走最平常的路线,也是只能上不能下。泽泽知道这些暗道在哪里,而且知道走到每个地方的所花费的时间。
现在你要做的就是算出泽泽走到金字塔顶端所花最少的时间。
注意:
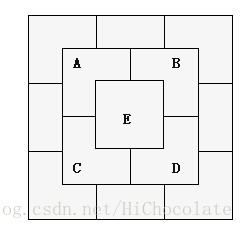
第n层第i行第j列我们表示成n,i,j。当n>=2时,n,i,j可以由4个位置走来(不包括暗道)。如3,1,1可以从2,1,1或2,1,2或2,2,1或2,2,2走来。
如图所示,一座大小为3的金字塔的俯视图就是这个样子的。从A(2,1,1)、B(2,1,2)、C(2,2,1)、D(2,2,2)都可以走到E(3,1,1)。其他位置依次类推。
输入
第1行为2个整数n,m。n表示金字塔的底部边长以及高,m表示有多少暗道。
接下来有n张正方形的图,每张图用一个回车隔开,表示从最底层到最高层的每个位置所花费的时间。保证上面的图的边长比下面图的多1。(如样例,这座大小为4的金字塔第1层是44的,第2层是33,第3层是22,第4层是11。)
接下来的m行,每行7个整数ai1,bi1,ci1,ai2,bi2,ci2,pi。表示第ai1层的第bi1行第ci1列到第ai2层的第bi2行第ci2列之间有一条时间为pi的暗道。保证ai1 < ai2。
输出
一个整数,即泽泽走到金字塔顶端的最短时间。
样例输入
4 2
4 1 5 2
4 3 4 7
1 9 2 8
0 3 5 1
2 8 5
9 3 9
1 1 8
7 4
5 2
42
1 1 2 2 3 1 1
1 3 2 2 2 1 7
样例输出
52
数据范围限制
提示
【样例说明】
流程:
1 泽泽一开始在1,1,1的位置,总时间为0+4=4。
2 从1,1,1走到1,1,2,总时间为4+1=5。
3 走暗道到了2,3,1,总时间为5+1+1=7。
4 从2,3,1走到2,3,2,总时间为7+1=8。
5 再上楼到了3,2,2,总时间为8+2=10。
6 再上楼到了4,1,1,总时间为10+42=52。
【限制】
对于50%的数据,n<=5
对于100%的数据,n<=100,m<=50,每格的暗道总数不超过10个。
题解:
本题有很多方法。
30%用bfs。
70%用我的方法。我是直接n^2的方法更新同一层的最小时间和更新上一层楼的最小时间和若是这个点为某个隧道入口,就更新这个隧道的出口。这个方法好似正解,但是被三个该死的数据坑了。那么就开始卡常。
70分程序:
uses math;
var
i,j,k,l,n,m,nx,ny,max:longint;
f,map:array[1..100,1..100,1..100] of longint;
st,ar:array[1..3,1..50] of longint;
ti:array[1..50] of longint;
pmfx:array[1..4,1..2] of longint=((-1,0),(0,-1),(1,0),(0,1));
upfx:array[1..4,1..2] of longint=((-1,-1),(0,-1),(-1,0),(0,0));
begin
assign(input,'egypt.in');reset(input);
assign(output,'egypt.out');rewrite(output);
readln(n,m);
max:=2139062147;
for i:=1 to n do
begin
for j:=1 to n-i+1 do
begin
for k:=1 to n-i+1 do
begin
read(map[i,j,k]);
end;
end;
end;
for i:=1 to m do
begin
readln(st[1,i],st[2,i],st[3,i],ar[1,i],ar[2,i],ar[3,i],ti[i]);
end;
fillchar(f,sizeof(f),127 div 3);
f[1,1,1]:=map[1,1,1];
for i:=1 to n do
begin
for j:=1 to n do
begin
for k:=1 to n do
begin
if (i=2)and(j=3)and(k=1) then
begin
max:=max;
end;
for l:=1 to m do
begin
if (i=st[1,l])and(j=st[2,l])and(k=st[3,l]) then
begin
f[ar[1,l],ar[2,l],ar[3,l]]:=min(f[ar[1,l],ar[2,l],ar[3,l]],ti[l]+f[i,j,k]+map[ar[1,l],ar[2,l],ar[3,l]]);
end;
end;
for l:=1 to 4 do
begin
nx:=j+pmfx[l,1];
ny:=k+pmfx[l,2];
if (nx>0)and(nx<=n-i+1)and(ny>0)and(ny<=n-i+1) then
begin
f[i,nx,ny]:=min(f[i,nx,ny],map[i,nx,ny]+f[i,j,k]);
end;
if i<n then
begin
nx:=j+upfx[l,1];
ny:=k+upfx[l,2];
if (nx>0)and(nx<=n-i)and(ny>0)and(ny<=n-i) then
begin
f[i+1,nx,ny]:=min(f[i+1,nx,ny],map[i+1,nx,ny]+f[i,j,k]);
end;
end;
end;
end;
end;
end;
writeln(f[n,1,1]);
close(input);close(output);
end.
100%:(水法)在一个数据:
01 01 01 01 01 01 01
99 99 99 99 99 99 01
01 01 01 01 01 99 01
01 99 99 99 01 99 01
01 99 01 01 01 99 01
01 99 99 99 99 99 01
01 01 01 01 01 01 01
这是不可以更新完全部的。
那么我就在更新完一次后,就反向更新,还是不可以,经过了4次反复更新,那么就AC了。其实数据如果认真一点出,那么本题就必须要用正解了。
卡常程序:
uses math;
var
i,j,k,l,n,m,nx,ny,max,p,g:longint;
f,map:array[1..100,1..100,1..100] of longint;
st,ar:array[1..3,1..50] of longint;
ti:array[1..50] of longint;
pmfx:array[1..4,1..2] of longint=((-1,0),(0,-1),(1,0),(0,1));
upfx:array[1..4,1..2] of longint=((-1,-1),(0,-1),(-1,0),(0,0));
begin
assign(input,'egypt.in');reset(input);
assign(output,'egypt.out');rewrite(output);
readln(n,m);
max:=2139062147;
for i:=1 to n do
begin
for j:=1 to n-i+1 do
begin
for k:=1 to n-i+1 do
begin
read(map[i,j,k]);
end;
end;
end;
for i:=1 to m do
begin
readln(st[1,i],st[2,i],st[3,i],ar[1,i],ar[2,i],ar[3,i],ti[i]);
end;
fillchar(f,sizeof(f),127 div 2);
f[1,1,1]:=map[1,1,1];
for i:=1 to n do
begin
for p:=1 to 2 do
begin
for j:=1 to n do
begin
for k:=1 to n do
begin
if (i=2)and(j=3)and(k=1) then
begin
max:=max;
end;
for l:=1 to m do
begin
if (i=st[1,l])and(j=st[2,l])and(k=st[3,l]) then
begin
f[ar[1,l],ar[2,l],ar[3,l]]:=min(f[ar[1,l],ar[2,l],ar[3,l]],ti[l]+f[i,j,k]+map[ar[1,l],ar[2,l],ar[3,l]]);
end;
end;
for l:=1 to 4 do
begin
nx:=j+pmfx[l,1];
ny:=k+pmfx[l,2];
if (nx>0)and(nx<=n-i+1)and(ny>0)and(ny<=n-i+1) then
begin
f[i,nx,ny]:=min(f[i,nx,ny],map[i,nx,ny]+f[i,j,k]);
end;
if i<n then
begin
nx:=j+upfx[l,1];
ny:=k+upfx[l,2];
if (nx>0)and(nx<=n-i)and(ny>0)and(ny<=n-i) then
begin
f[i+1,nx,ny]:=min(f[i+1,nx,ny],map[i+1,nx,ny]+f[i,j,k]);
end;
end;
end;
end;
end;
for j:=n downto 1 do
begin
for k:=n downto 1 do
begin
if (i=2)and(j=3)and(k=1) then
begin
max:=max;
end;
for l:=1 to m do
begin
if (i=st[1,l])and(j=st[2,l])and(k=st[3,l]) then
begin
f[ar[1,l],ar[2,l],ar[3,l]]:=min(f[ar[1,l],ar[2,l],ar[3,l]],ti[l]+f[i,j,k]+map[ar[1,l],ar[2,l],ar[3,l]]);
end;
end;
for l:=1 to 4 do
begin
nx:=j+pmfx[l,1];
ny:=k+pmfx[l,2];
if (nx>0)and(nx<=n-i+1)and(ny>0)and(ny<=n-i+1) then
begin
f[i,nx,ny]:=min(f[i,nx,ny],map[i,nx,ny]+f[i,j,k]);
end;
if i<n then
begin
nx:=j+upfx[l,1];
ny:=k+upfx[l,2];
if (nx>0)and(nx<=n-i)and(ny>0)and(ny<=n-i) then
begin
f[i+1,nx,ny]:=min(f[i+1,nx,ny],map[i+1,nx,ny]+f[i,j,k]);
end;
end;
end;
end;
end;
end;
end;
writeln(f[n,1,1]);
close(input);close(output);
end.
100分正解:
很明显,这道题一看就知道用搜索,纯DP是不可能的,因为题目不符合无后效性,所以,我就考虑搜索。
方法就是DFS+记忆化,超时70…
仔细一想,dfs确实有些不妥,即使加了一大堆剪枝还是超(为什么不妥我就不解释了,233)
我马上把dfs改成了bfs(代码类似spfa核心代码,本蒟蒻就是从那儿得到灵感,实际上喝杯水醒醒大脑才觉得那应该叫记忆化。。。)
一改,觉得肯定AC了,谁知突然蹦出一个超时%90.
smg?
好吧,我承认我看着自己的代码看了3个小时,睡觉想了两个小时,硬是没任何进展。好咯,唯一的方法,打表,233…
好吧,当我打了表之后,我看了看众多神犇的方法,奇怪,与我的方法一模一样啊,真的一模一样啊,怎么会错呢?于是乎,我几乎把代码改了一半了,还是超时,这什么鬼啊 。。。。。。。。。。
最后,在刚刚过去的20分钟里,我突然发现了一个重大的问题,我是用集合判断边界,也就是判断x,y是否在[1…n]里。。。。。。。。。。。。。。。。。。。。。。。。。。
这就是著名的卡常数。。。。
我(ri)很(ni)伤(da)心(ye)
好吧,我改了判断边界之后就妥妥的AC了。。
优化:
我这里的bfs是最暴力的一种,一直往外拓展可能拓展的节点,直道拓展不了为止,但这样子做如果数据再极端一点的话,有可能导致你当前从一个原始节点拓展一个节点x,反而这个节点x一直往外拓展的时候最后还有可能把原始节点给更新了,这种情况如果重复出现的话,队列就要开到很大,即使用循环队列也得担心时间的问题。
所以我们可以想想优化,首先,第一层很明显不可能由第零层得来,也不可能由暗道得来,所以我们只需对第一层往四周拓展的bfs即可。
于是乎,对于第二层的每个节点,我们很明显可以选一个从第一层拓展到这个节点的最短路径,这里非常需要注意的是不需要第一层的每个节点都来更新第二层的节点,不然会答案错误,我们只需选择第一层能直接到达第二层某个节点的节点来更新第二层的某个节点(好好理解这句话。。。。233)
做完这个类似DP的步骤时,我们则可以看看这些节点是否能由暗道通往,如果有暗道通往的话又把他更新一次,这样更新完之后,我们可以得到一个可观的答案,我们再对这些答案进行类似第一层的操作,则可以得到正确答案了,很明显,这种方法的正确性是很容易得到类似证明的证明。
时间复杂度接近0.1s
标程:
type
re=record
x,y:longint;
end;
const
d:array[1..4,1..2] of longint=((1,0),(-1,0),(0,1),(0,-1));
var
f:Array[1..100,1..100,1..100,0..10,0..4] of longint;
dis,a:array[1..100,1..100,1..100] of longint;
data:array[1..100000] of re;
n,m,i,j,k,head,tail,xx,yy,x,y,ai1,bi1,ci1,ai2,bi2,ci2,pi,len:longint;
procedure getans(t:Longint);
begin
for x:=1 to n-t+1 do
for y:=1 to n-t+1 do
begin
head:=0;
tail:=1;
data[1].x:=x;
data[1].y:=y;
while head<tail do
begin
inc(head);
for k:=1 to 4 do
begin
xx:=data[head].x+d[k,1]; yy:=data[head].y+d[k,2];
if (xx>0) and (xx<=n-t+1) and (yy>0) and (yy<=n-t+1) and (dis[t,xx,yy]>dis[t,data[head].x,data[head].y]+a[t,xx,yy]) then
begin
dis[t,xx,yy]:=dis[t,data[head].x,data[head].y]+a[t,xx,yy];
inc(tail);
data[tail].x:=xx;
data[tail].y:=yy;
end;
end;
end;
end;
end;
function min(x,y:longint):longint;
begin
if x<y then exit(x) else exit(y);
end;
begin
assign(input,'egypt.in'); reset(input);
assign(output,'egypt.out'); rewrite(output);
readln(n,m);
for i:=1 to n do
for j:=1 to n-i+1 do
for k:=1 to n-i+1 do
read(a[i,j,k]);
for i:=1 to m do
begin
readln(ai1,bi1,ci1,ai2,bi2,ci2,pi);
inc(f[ai2,bi2,ci2,0,0]);
len:=f[ai2,bi2,ci2,0,0];
f[ai2,bi2,ci2,len,1]:=ai1;
f[ai2,bi2,ci2,len,2]:=bi1;
f[ai2,bi2,ci2,len,3]:=ci1;
f[ai2,bi2,ci2,len,4]:=pi;
end;
fillchar(dis,sizeof(dis),8);
dis[1,1,1]:=a[1,1,1];
getans(1);
for i:=2 to n do
begin
for x:=1 to n-i+1 do
for y:=1 to n-i+1 do
begin
dis[i,x,y]:=min(min(min(dis[i-1,x,y],dis[i-1,x+1,y]),dis[i-1,x,y+1]),dis[i-1,x+1,y+1]);
inc(dis[i,x,y],a[i,x,y]);
for k:=1 to f[i,x,y,0,0] do
begin
j:=f[i,x,y,k,1]; xx:=f[i,x,y,k,2]; yy:=f[i,x,y,k,3];
dis[i,x,y]:=min(dis[i,x,y],dis[j,xx,yy]+a[i,x,y]+f[i,x,y,k,4]);
end;
end;
getans(i);
end;
writeln(dis[n,1,1]);
close(input); close(output);
end.