拷贝SD卡的文件,去升级app,为了验证文件一致性,想到用MD5。于是记录一下MD5的特点和大概原理。
MD5算法具有以下特点:
1、压缩性:任意长度的数据,算出的MD5值长度都是固定的。
2、容易计算:从原数据计算出MD5值很容易。
3、抗修改性:对原数据进行任何改动,哪怕只修改1个字节,所得到的MD5值都有很大区别。
4、强抗碰撞:已知原数据和其MD5值,想找到一个具有相同MD5值的数据(即伪造数据)是非常困难的。
MD5原理
1.1 数据补齐 / 填充(Padding)
MD5 可以认为是基于 block 的算法:它要求每次处理的数据长度为 512bits。但是实际中要处理的明文长度并不一定是 512 的整数倍,怎么办呢?参考 AES 的做法,做数据补齐 / 填充(Padding)。假设原始明文消息的长度为 K,MD5 的 Padding 可以细分为 2 个子步骤:
- 附加填充位(Append Padding Bits):从原始明文消息的 K 位之后补 100... 一直到 512-64=448 位,填充位的规则是:只有第一个 bit 是 1,之后都是 0。这里有个问题:如果 K%512 正巧等于 448 怎么办呢?再者,如果 K%512 在 [448,512(模运算得到的是 0)] 之间怎么办呢?答案:Append Padding Bits 要求至少填充 1 位,如果长度正好是 448,那么就索性再增加一个 block,填充
512bits;如果模超过 448,也再增加一个 block,填充512-(K%512-448);同理,如果模不到 448,就填充448-K%512即可。 - 附加长度(Append Length):这个时候,最后一个 block 只剩下 64bits 需要填充了,其内容是原始明文的长度。试想,64bits 可以表示最长的数据将近 2^30GB 的数据了!如果原始明文大于这个数值,那就只能对 2^64 取模,作者在原文中是这么写的:
In the unlikely event that b is greater than 2^64, then only the low-order 64 bits of b are used.
如果 b 大于 2^64,则仅使用 b 的低阶 64 位。
整个 Padding 的示意图如下所示:

1.2 Initialize MD Buffer 初始化 MD 缓冲区
MD Buffer 是 4 个 32bits(=4bytes)的向量,准确来说是 word。RFC 原文对 MD Buffer 的初始化描述如下:
A four-word buffer (A,B,C,D) is used to compute the message digest. Here each of A, B, C, D is a 32-bit register. These registers are initialized to the following values in hexadecimal, low-order bytes first):
word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10
一个 4-word 的缓冲区(A、B、C、D)用来产生消息摘要,这里 A、B、C、D 都是 32bits 的寄存器,这些寄存器被初始化为以下值(十六进制,低位字节在前):
word A: 01 23 45 67
word B: 89 ab cd ef
word C: fe dc ba 98
word D: 76 54 32 10
必须要【敲黑板】的是文章明确表示:低字节在前,这也就意味着真实代码中存储的时候是(请注意顺序):
unsigned int A = 0x67452301;
unsigned int B = 0xEFCDAB89;
unsigned int C = 0x98BADCFE;
unsigned int D = 0x10325476;
1.3 Process Message in 16-Word Blocks 处理消息组
这一步绝对是整个 MD5 算法最绕的地方,看了很多网上的文章,越看越绕,看了 md5 的好多代码实现后终于明白了。 摘要的算法都是让每一个 bit 都生成不同的决策分枝,先祭出 Wikipedia 的图:
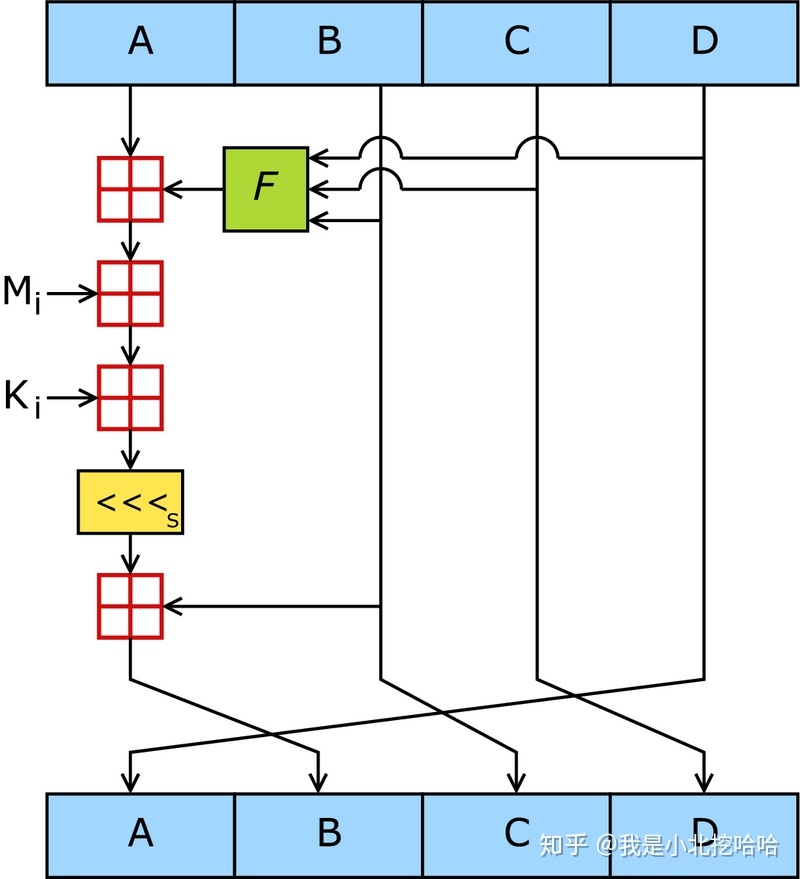
说实话,乍看这个图并不清楚发生了什么。一步步来解释,在此之前必须了解图中每个字母所代表的的含义:
- 明文 M:图中 M_i 是一个 32bits 的明文数据,跟 A/B/C/D 长度相同,也是一个 word 的大小。问题来了:一个 block 不是 512bits 吗?那怎么这里只有 32bits 呢?回答:所以 MD5 对一个 block 数据要进行 16 次(512/32)完全相同的一套完整操作,一套完整的操作包括 4 轮向量运算。也就是说,每 32bits 明文数据为一个单位,要进行 4 轮的向量运算;而每一个 block 要对 16 个(32bits)单位明文数据进行运算,共计 64 次。
- 正弦函数表(sine table)K:sine table 共有 64 个常量数值,每个数值长度 32bits,图中 K_i 就是就是这个 sine table。笔者指出一点:图中的下标是有问题的,K_i 和 M_i 容易让人产生误解,以为明文和 sine table 的循环顺序一致,实际上两者遍历的顺序不一致!sine table 的内容如下:
const unsigned int k[] = {
0xd76aa478, 0xe8c7b756, 0x242070db, 0xc1bdceee, 0xf57c0faf, 0x4787c62a, 0xa8304613, 0xfd469501,
0x698098d8, 0x8b44f7af, 0xffff5bb1, 0x895cd7be, 0x6b901122, 0xfd987193, 0xa679438e, 0x49b40821,
0xf61e2562, 0xc040b340, 0x265e5a51, 0xe9b6c7aa, 0xd62f105d, 0x02441453, 0xd8a1e681, 0xe7d3fbc8,
0x21e1cde6, 0xc33707d6, 0xf4d50d87, 0x455a14ed, 0xa9e3e905, 0xfcefa3f8, 0x676f02d9, 0x8d2a4c8a,
0xfffa3942, 0x8771f681, 0x6d9d6122, 0xfde5380c, 0xa4beea44, 0x4bdecfa9, 0xf6bb4b60, 0xbebfbc70,
0x289b7ec6, 0xeaa127fa, 0xd4ef3085, 0x04881d05, 0xd9d4d039, 0xe6db99e5, 0x1fa27cf8, 0xc4ac5665,
0xf4292244, 0x432aff97, 0xab9423a7, 0xfc93a039, 0x655b59c3, 0x8f0ccc92, 0xffeff47d, 0x85845dd1,
0x6fa87e4f, 0xfe2ce6e0, 0xa3014314, 0x4e0811a1, 0xf7537e82, 0xbd3af235, 0x2ad7d2bb, 0xeb86d391};
至于 sine table 是怎么生成的,推荐阅读:MD5 implementation notes。
- 位移 S:MD5 定义了一个 shift 或者说是 rotate 操作,RFC 原文描述如下:
Let X <<<s denote the 32-bit value obtained by circularly shifting (rotating) X left by s bit positions.
令 X <<< s 表示通过将 X 向左循环移位(旋转)s 个位位置而获得的 32 位值。
位移 S 共有 16 个常量数值:
round 1: 7, 12, 17, 22
round 2: 5, 9, 14, 20
round 3: 4, 11, 16, 23
round 4: 6, 10, 15, 21
- 非线性函数 F:函数 F 是整个 MD5 算法中唯一非线性变换,虽然图中只写了 F,但其实 F 有 4 种形式,有的文章会分别描述为 F、G、H 和 I 函数(或者是 FFGGHHII):
round 1: F(x,y,z) = (x & y) | (~x & z)
round 2: G(x,y,z) = (x & z) | (y & ~z)
round 3: H(x,y,z) = x ^ y ^ z
round 4: I(x,y,z) = y ^ ( x | ~z)
对于一个 M_i 而言,都会经历这 4 轮操作。
- 四个数据处理函数
Mj表示第M组第j个int数
FF(a,b,c,d,Mj,s,ti)表示a=b+((a+F(b,c,d)+Mj+ti)<<<s)
GG(a,b,c,d,Mj,s,ti)表示a=b+((a+G(b,c,d)+Mj+ti)<<<s)
HH(a,b,c,d,Mj,s,ti)表示a=b+((a+H(b,c,d)+Mj+ti)<<<s)
II(a,b,c,d,Mj,s,ti)表示a=b+((a+I(b,c,d)+Mj+ti)<<<s)
第一轮
a=FF(a,b,c,d,M0,7,0xd76aa478)
b=FF(d,a,b,c,M1,12,0xe8c7b756)
c=FF(c,d,a,b,M2,17,0x242070db)
d=FF(b,c,d,a,M3,22,0xc1bdceee)
a=FF(a,b,c,d,M4,7,0xf57c0faf)
b=FF(d,a,b,c,M5,12,0x4787c62a)
c=FF(c,d,a,b,M6,17,0xa8304613)
d=FF(b,c,d,a,M7,22,0xfd469501)
a=FF(a,b,c,d,M8,7,0x698098d8)
b=FF(d,a,b,c,M9,12,0x8b44f7af)
c=FF(c,d,a,b,M10,17,0xffff5bb1)
d=FF(b,c,d,a,M11,22,0x895cd7be)
a=FF(a,b,c,d,M12,7,0x6b901122)
b=FF(d,a,b,c,M13,12,0xfd987193)
c=FF(c,d,a,b,M14,17,0xa679438e)
d=FF(b,c,d,a,M15,22,0x49b40821)
第二轮
a=GG(a,b,c,d,M1,5,0xf61e2562)
b=GG(d,a,b,c,M6,9,0xc040b340)
c=GG(c,d,a,b,M11,14,0x265e5a51)
d=GG(b,c,d,a,M0,20,0xe9b6c7aa)
a=GG(a,b,c,d,M5,5,0xd62f105d)
b=GG(d,a,b,c,M10,9,0x02441453)
c=GG(c,d,a,b,M15,14,0xd8a1e681)
d=GG(b,c,d,a,M4,20,0xe7d3fbc8)
a=GG(a,b,c,d,M9,5,0x21e1cde6)
b=GG(d,a,b,c,M14,9,0xc33707d6)
c=GG(c,d,a,b,M3,14,0xf4d50d87)
d=GG(b,c,d,a,M8,20,0x455a14ed)
a=GG(a,b,c,d,M13,5,0xa9e3e905)
b=GG(d,a,b,c,M2,9,0xfcefa3f8)
c=GG(c,d,a,b,M7,14,0x676f02d9)
d=GG(b,c,d,a,M12,20,0x8d2a4c8a)
第三轮
a=HH(a,b,c,d,M5,4,0xfffa3942)
b=HH(d,a,b,c,M8,11,0x8771f681)
c=HH(c,d,a,b,M11,16,0x6d9d6122)
d=HH(b,c,d,a,M14,23,0xfde5380c)
a=HH(a,b,c,d,M1,4,0xa4beea44)
b=HH(d,a,b,c,M4,11,0x4bdecfa9)
c=HH(c,d,a,b,M7,16,0xf6bb4b60)
d=HH(b,c,d,a,M10,23,0xbebfbc70)
a=HH(a,b,c,d,M13,4,0x289b7ec6)
b=HH(d,a,b,c,M0,11,0xeaa127fa)
c=HH(c,d,a,b,M3,16,0xd4ef3085)
d=HH(b,c,d,a,M6,23,0x04881d05)
a=HH(a,b,c,d,M9,4,0xd9d4d039)
b=HH(d,a,b,c,M12,11,0xe6db99e5)
c=HH(c,d,a,b,M15,16,0x1fa27cf8)
d=HH(b,c,d,a,M2,23,0xc4ac5665)
第四轮
a=II(a,b,c,d,M0,6,0xf4292244)
b=II(d,a,b,c,M7,10,0x432aff97)
c=II(c,d,a,b,M14,15,0xab9423a7)
d=II(b,c,d,a,M5,21,0xfc93a039)
a=II(a,b,c,d,M12,6,0x655b59c3)
b=II(d,a,b,c,M3,10,0x8f0ccc92)
c=II(c,d,a,b,M10,15,0xffeff47d)
d=II(b,c,d,a,M1,21,0x85845dd1)
a=II(a,b,c,d,M8,6,0x6fa87e4f)
b=II(d,a,b,c,M15,10,0xfe2ce6e0)
c=II(c,d,a,b,M6,15,0xa3014314)
d=II(b,c,d,a,M13,21,0x4e0811a1)
a=II(a,b,c,d,M4,6,0xf7537e82)
b=II(d,a,b,c,M11,10,0xbd3af235)
c=II(c,d,a,b,M2,15,0x2ad7d2bb)
d=II(b,c,d,a,M9,21,0xeb86d391)
- MD Buffer:MD Buffer 就是 A、B、C、D,笔者认为 MD5 的核心就是不断对 MD Buffer 做线性、非线性向量变换,最终得到消息摘要。一个 block 共计 64 次的操作,指的就是对 MD Buffer 的操作。而整个明文操作下来应该有 N*64(N 是明文数据 Padding 之后整除 512 的数值),最终得到了信息摘要,过程如下图:
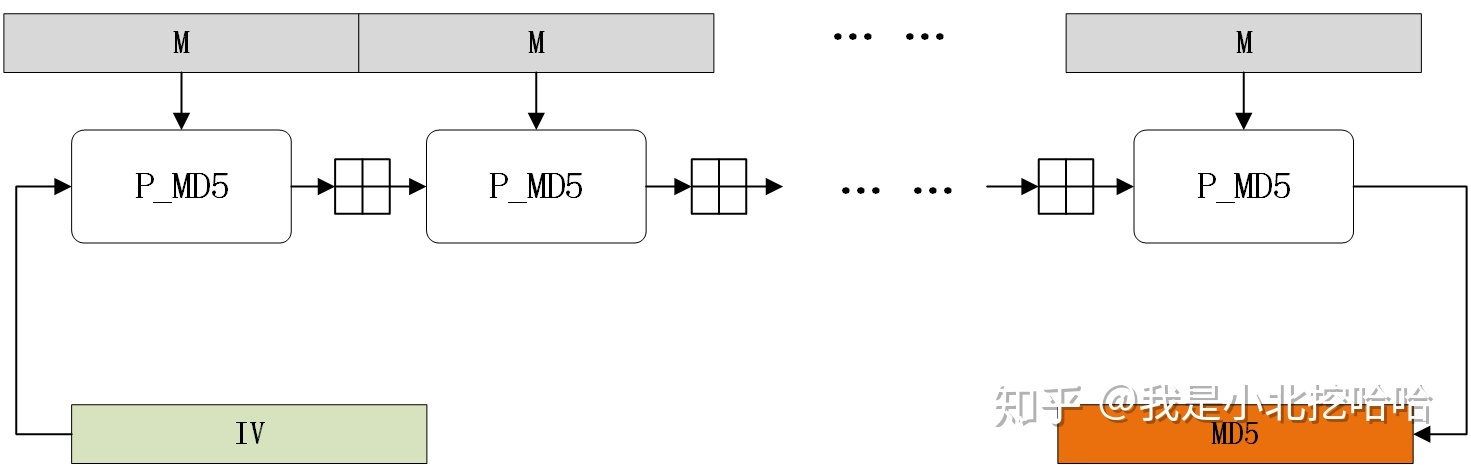
了解以上几个关键点,对整个 MD5 的加密过程应该也基本有概念了,这个时候推荐回到 RFC 再去阅读 Rivest 给出的 C 代码实现。
算法的另一种讲解:
大体上来说,信息摘要基本的算法是把信息分成多个部分,每次计算一部分。
摘要 =(初始值或上次的摘要 + 一部分信息 + 固定值) << 移动一定位数
MD5 把 512b 分成 16 个 32b 块来计算。MD5 生成 32b 摘要,需要计算 16 次。为了让固定值能比较随机,MD5 使用了一个 sin(1) 到 sin(16) 的整数部分。而移动的位数也不是固定一个数,而是 4 个,循环使用。固定值计算如下:
MD(md, n) =(md + M(n)+ abs(sin(n)) << shift(n % 4)
如果要生成 128b 的 MD,只需要每次 MD 的不同部分参与运算。生成 128b 需要四轮,共计算 64 次。为了让这 128 位有所关联,MD5 分别用四种不同的非线性算法计算了四轮。
我们先看第一轮,它的非线性算法是 F(x,y,z)=(x&y)|((~x)&z)。这个算法有三个参数,而 128b 摘要可分成 4 个 32b 组,分别可称为 a,b,c,d. 第一次需要计算 a, 就由其它三个值参与计算,结果再加上 a,做为计算下一个 MD 的初始值。再下次就轮转。
md = a + F(b, c, d)
md = b + F(c, d, a)
md = c + F(d, a, b)
md = d + F(a, b, c)
后面四轮的非线性算法是
F(x,y,z) = (x & y) | (~x & z)
G(x,y,z) = (x & z) | (y & ~z)
H(x,y,z) = x ^ y ^ z
I(x,y,z) = y ^ ( x | ~z)
对应的移位数组是
0~15次 [7, 12, 17, 22]
16~31次 [5, 9, 14, 20]
32~47次 [4, 11, 16, 23]
48~63次 [6, 10, 15, 21]
而选取 n 的次序也不一样
0~15次 n = i
16~31次 n = (5*i+1) % 16
32~47次 n = (3*i+1) % 16
48~63次 n = (7*i+1) % 16
//Note: All variables are unsigned 32 bits and wrap modulo 2^32 when calculating
var int[64] r, k
//r specifies the per-round shift amounts
r[ 0..15]:= {7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22, 7, 12, 17, 22}
r[16..31]:= {5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20, 5, 9, 14, 20}
r[32..47]:= {4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23, 4, 11, 16, 23}
r[48..63]:= {6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21, 6, 10, 15, 21}
//Use binary integer part of the sines of integers as constants:
for i from 0 to 63
k[i] := floor(abs(sin(i + 1)) × 2^32)
//Initialize variables:
var int h0 := 0x67452301
var int h1 := 0xEFCDAB89
var int h2 := 0x98BADCFE
var int h3 := 0x10325476
//Pre-processing:
append "1" bit to message
append "0" bits until message length in bits ≡ 448 (mod 512)
append bit length of message as 64-bit little-endian integer to message
//Process the message in successive 512-bit chunks:
for each 512-bit chunk of message
break chunk into sixteen 32-bit little-endian words w[i], 0 ≤ i ≤ 15
//Initialize hash value for this chunk:
var int a := h0
var int b := h1
var int c := h2
var int d := h3
//Main loop:
for i from 0 to 63
if 0 ≤ i ≤ 15 then
f := (b and c) or ((not b) and d)
g := i
else if 16 ≤ i ≤ 31
f := (d and b) or ((not d) and c)
g := (5×i + 1) mod 16
else if 32 ≤ i ≤ 47
f := b xor c xor d
g := (3×i + 5) mod 16
else if 48 ≤ i ≤ 63
f := c xor (b or (not d))
g := (7×i) mod 16
temp := d
d := c
c := b
b := leftrotate((a + f + k[i] + w[g]),r[i]) + b
a := temp
Next i
//Add this chunk's hash to result so far:
h0 := h0 + a
h1 := h1 + b
h2 := h2 + c
h3 := h3 + d
End ForEach
var int digest := h0 append h1 append h2 append h3 //(expressed as little-endian)
1.5 Output 输出
输出这个小节也没啥具体可交代的,最后得到的 MD Buffer 就是信息摘要了。