编译原理之理解语法树、短语、直接短语和句柄

短语
书上的定义如下: 

书上写的比较抽象，我这里简单解释一下，有两个文法，分别是：

S=*=>aAp (由于部分字符难以输入，在此用a,b,p代替)
A=+=>b

我们由此可以画出他的抽象语法树，如下:

 

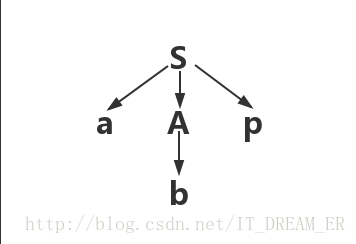
那么，abp为此句型的短语 
总结来说：一个句型的语法树中任一子树叶结点所组成的符号串都是该句型的短语，由这概念，那么我们自然可以想到，b也应该是该句型的一个短语。

直接短语
书中的定义：

 

书中的意思总结来说，指的是如果子树中不再包含其他的子树，即A只能推导出b，而b不能再推出其他的式子，则b为此句型的直接短语

句柄
先来看一下书中的定义:

 

书中的意思就是：直接短语中的最左直接短语为该句型的句柄。

小练习

1.已知文法：

S->a|^|(T)

T->T,S|S

分析句型（T,(^,a))，求全部的短语、直接短语和句柄。

S -> (T) -> (T, S) -> (T, (T)) -> (T, (T, S)) -> (T, (S,S)) -> (T, (^, S)) ->（T, (^, a))

此文法的抽象语法树为:

 

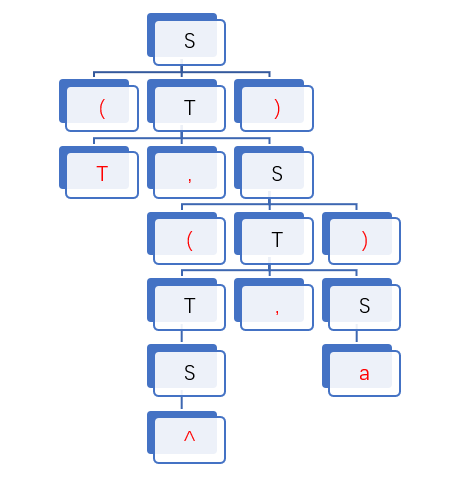
由此可得S=(S, (T), b)为此文法的一个句型：

• 短语: ^; a; ^, a; (^, a); T, (^, a); （T, (^, a));
  

• 直接短语:^; a;

• 句柄:^

• 此时的最左直接短语是^所以句柄为^

 

2.构造上下文无关文法，描述语言：

（1）｛aⁿbⁿ|n>=0｝

　　　　a, b个数相等，即可得
　　　　　　S -> aSb l ab | ε

（2）｛a^mbⁿ|m>=n>=0｝

　　　　a个数大于b，即可得　　　　

　　　　　　S -> aS l A

　　　　　　A -> aAb | ε

（3）｛(ab)ⁿ|n>=0｝

　　A -> ab

　　S -> (A)S | ε

（4）｛a^mbⁿ|m,n>=1｝

　　S -> aSb|aS|Sb|ab

（5）if语句

　　if  => if <条件> then <语句A> | if <条件> then <语句B> else <语句B>

3.如果if语句的方法：

stmt -> if expr then stmt

     | if expr then stmt else stmt

     | other

句子if E1 then if E2 then S1 else S2是否有两棵不同的语法树？说明了什么？

　　有两颗语法树，分别如图

 

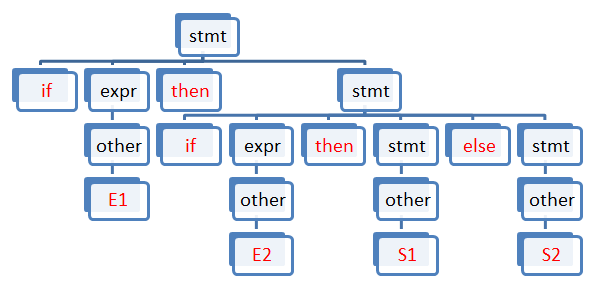
 说明原语法树是二义的

参考链接：https://blog.csdn.net/m0_37154839/article/details/80229211