机器学习数学部分常用相关概念:
高等数学
1)函数
2)极限
3)导数
4)极值和最值
5)泰勒级数
6)梯度
7)梯度下降
线性代数
1)基本概念
2)行列式
3)矩阵
4)最小二乘法
5)向量的线性相关性
概率论
1)事件
2)排列组合
3)概率
4)贝叶斯定理
5)概率分布
6)期望和方差
7)参数估计
视频学习内容:点我
1)P2 概率论与贝叶斯先验
2)P3 矩阵和线性代数
机器学习是一门多领域交叉学科,涉及较多的数学知识,本节课知识之前都有学过,这次根据重点重新梳理一遍,一定要多加重视。通过观看视频,大家对课程的数学基础部分加深印象。
建议大家边看边做笔记,记录要点及所在时间点,以便有必要的时候回看。学习笔记也是作业的一部分。
要求
(1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
1)P2 概率论与贝叶斯先验
视频中学习的笔记记录(公式)


2)P3 矩阵和线性代数
矩阵和线性代数主要内容有如下几点: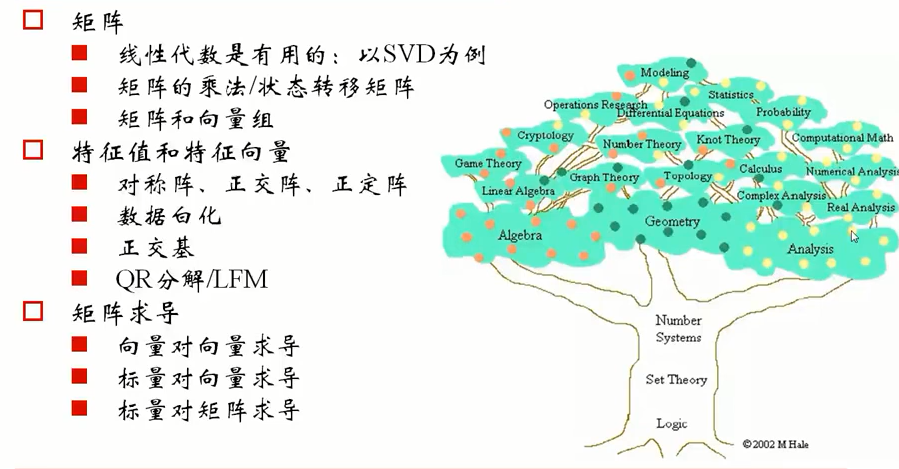
用到的线性代数知识有:
1.方阵的行列式之间的运算
2.代数余子式
3.范德蒙行列式Vandermonde
4.矩阵的乘法
5.矩阵的秩
6.秩与线性方程组的解的关系
7.正交阵
8.特征值和特征向量
9.正定阵
(2)用自己的话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。简单说在单变量的实值函数的情况,梯度只是导数,或者,对于一个线性代数,也就是线的斜率。
梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降是最常采用的方法之一。简单说就是从山顶上找一个最快,最陡峭的路线下山。
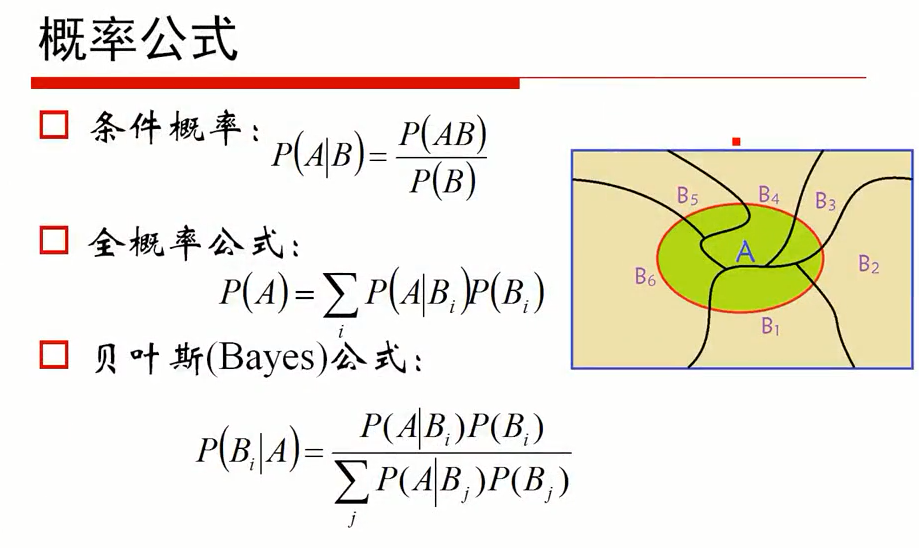
贝叶斯定理:贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因(即大事件A已经发生的条件下,分割中的小事件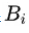
的概率),设
是样本空间Ω的一个划分,则对任一事件A(P(A)>0),有贝叶斯定理:
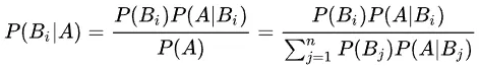
对于特征集合x,我们想要知道样本在这个特征集合x下属于哪个类别,即求后验概率P(c|x)最大的类标记。这样基于贝叶斯公式,可以得到:
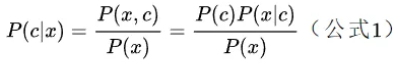
贝叶斯定理是用来描述两个条件概率之间关系的定理,比如P(A|B)和P(B|A),通常,事件A在事件B发生的条件下的概率{P(A|B)}与事件B在事件A的条件下的概率{P(B|A)}是不一样的,但是这两者之间有确定的关系,贝叶斯法则就是这种关系的陈述。