Eat the Trees hdu 1693

Problem Description
Most of us know that in the game called DotA(Defense of the Ancient), Pudge is a strong hero in the first period of the game. When the game goes to end however, Pudge is not a strong hero any more.
So Pudge’s teammates give him a new assignment—Eat the Trees!

The trees are in a rectangle N * M cells in size and each of the cells either has exactly one tree or has nothing at all. And what Pudge needs to do is to eat all trees that are in the cells.
There are several rules Pudge must follow:
I. Pudge must eat the trees by choosing a circuit and he then will eat all trees that are in the chosen circuit.
II. The cell that does not contain a tree is unreachable, e.g. each of the cells that is through the circuit which Pudge chooses must contain a tree and when the circuit is chosen, the trees which are in the cells on the circuit will disappear.
III. Pudge may choose one or more circuits to eat the trees.

Now Pudge has a question, how many ways are there to eat the trees?
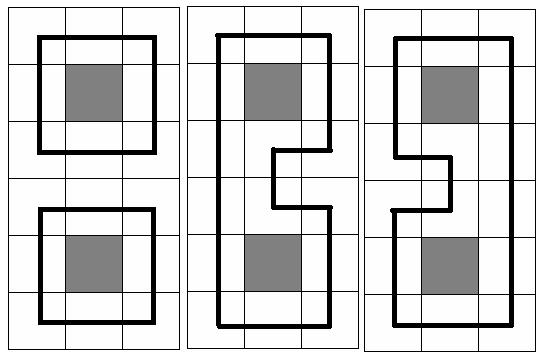
At the picture below three samples are given for N = 6 and M = 3(gray square means no trees in the cell, and the bold black line means the chosen circuit(s))

 

Input
The input consists of several test cases. The first line of the input is the number of the cases. There are no more than 10 cases.
For each case, the first line contains the integer numbers N and M, 1<=N, M<=11. Each of the next N lines contains M numbers (either 0 or 1) separated by a space. Number 0 means a cell which has no trees and number 1 means a cell that has exactly one tree.

Output
For each case, you should print the desired number of ways in one line. It is guaranteed, that it does not exceed 263 – 1. Use the format in the sample.

Sample Input
2
6 3
1 1 1
1 0 1
1 1 1
1 1 1
1 0 1
1 1 1
2 4
1 1 1 1
1 1 1 1

Sample Output
Case 1: There are 3 ways to eat the trees.
Case 2: There are 2 ways to eat the trees.

最简单的插头dp

题目大意

给出一个M*N的地图，部分格子是障碍。
现把所有非障碍格子连起来，要求每个格子有且仅有有两个相邻格子与之相连，
问有多少种方案。
(N,M<=11)

插头dp的两个重要元素就是插头和决策线（这个还是去看论文吧）

主要就是讨论换行的情况和不换行的情况

然后就是讨论那个凸角的情况，还有当前决策的格子是不是障碍物，仔细一点就没问题了

被hdu坑了，pascal不能用<<，忘记用int64结果WA了，还好测了一下大数据发现了

var
    f:array[0..12,0..12,0..4096]of int64;
    a:array[0..12,0..12]of longint;
    n,m,time,t:longint;

procedure init;
var
    i,j:longint;
begin
    fillchar(f,sizeof(f),0);
    fillchar(a,sizeof(a),0);
    read(n,m);
    for i:=1 to n do
      for j:=1 to m do
        read(a[i,j]);
    f[0,m,0]:=1;
end;

procedure work;
var
    i,j,k:longint;
begin
    for i:=1 to n do
      for j:=1 to m do
        if j=1 then
          begin
            if a[i,j]=1 then
              for k:=0 to 1 shl m-1 do
                if k and 1=0 then inc(f[i,j,k shl 1+3],f[i-1,m,k])
                else
                  begin
                    inc(f[i,j,k shl 1],f[i-1,m,k]);
                    inc(f[i,j,k shl 1-1],f[i-1,m,k]);
                  end
            else
              for k:=0 to 1 shl m-1 do
                if k and 1=0 then inc(f[i,j,k shl 1],f[i-1,m,k]);
          end
        else
          begin
            if a[i,j]=1 then
              for k:=0 to 1 shl (m+1)-1 do
                if k and(1 shl (j-1))>0 then
                  if k and(1 shl j)>0 then inc(f[i,j,k-3 shl (j-1)],f[i,j-1,k])
                  else
                    begin
                      inc(f[i,j,k],f[i,j-1,k]);
                      inc(f[i,j,k+1 shl (j-1)],f[i,j-1,k]);
                    end
                else
                  if k and(1 shl j)>0 then
                    begin
                      inc(f[i,j,k],f[i,j-1,k]);
                      inc(f[i,j,k-1 shl (j-1)],f[i,j-1,k]);
                    end
                  else inc(f[i,j,k+3 shl (j-1)],f[i,j-1,k])
            else
              for k:=0 to 1 shl (m+1)-1 do
                if k and(3 shl (j-1))=0 then inc(f[i,j,k],f[i,j-1,k]);
          end;
    writeln('Case ',time,': There are ',f[n,m,0],' ways to eat the trees.');
end;

begin
    read(t);
    for time:=1 to t do
      begin
        init;
        work;
      end;
end.