回归不同于分类,回归是根据给定数据进行预测,例如销售量预测或者名人离婚率预测等。
1.线性回归
如果是一组二维数据,即标准的一组(x,y)数据集,使用标准线性回归就是找到一根直线能最好的拟合这组数据,使其误差最小,如下图所示:
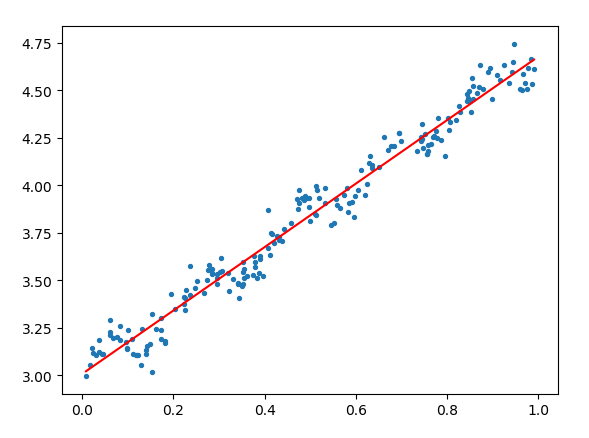
如果给定数据是多维,线性回归意味着将输入项分别乘上一些常量,将结果相加,就可以得到输出。
主要任务便是求取这个权重矩阵W,使预测值y与与真实值y之间的误差值最小。
经过一系列数学骚操作(有兴趣可以查下自己推导),最后能使误差最小的权重矩阵:
python实战里面标准线性回归案例程序(结果为上图):

1 from numpy import * 2 import matplotlib.pyplot as plt 3 4 # 自适应数据加载函数 5 def loadDataSet(fileName): 6 numFeat=len(open(fileName).readline().split(' ')) 7 dataMat=[];labelMat=[] 8 fr=open(fileName) 9 for line in fr.readlines(): 10 lineArr=[] 11 curLine=line.strip().split(' ') 12 for i in range(numFeat-1): 13 lineArr.append(float(curLine[i])) 14 dataMat.append(lineArr) 15 labelMat.append(float(curLine[-1])) 16 return dataMat,labelMat 17 18 # 计算当前数据的回归系数最优解 19 def standRegres(xArr,yArr): 20 xMat=mat(xArr) 21 yMat=mat(yArr).T 22 xTx=xMat.T*xMat 23 if linalg.det(xTx)==0.0: 24 print("this matrix is singular,cannot do inverse") 25 return 26 ws=xTx.I*(xMat.T*yMat) 27 return ws 28 29 # 标准线性回归画图 30 def drawStand(xMat,yMat,ws): 31 fig=plt.figure() 32 ax=fig.add_subplot(111) 33 # flatten().A[0] 能将二维转换为一维 34 ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0]) 35 yHat=xMat*ws 36 ax.plot(xMat[:,1],yHat) 37 plt.show() 38 39 abX,abY=loadDataSet('ex0.txt') 40 ws=standRegres(abX,abY) 41 drawStand(mat(abX),mat(abY),ws)
2. 局部加权线性回归(LWLR)
当我们直接使用标准的线性回归时,很容易欠拟合,即不能很好描述数据情况,其本质原因是我们用的最小均方误差进行无偏估计。我们可以使用局部加权线性回归来解决这个问题,就1中的问题,大家可以随意感受一下。局部加权线性回归也引入了一个问题,增加了计算量,对每个点预测时都必须使用整个数据集。
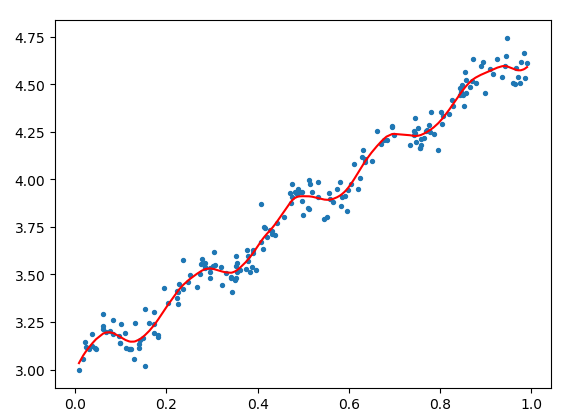
局部加权的线性规划的回归系数如下:
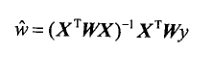
我们可以很快瞄到这里多了一个W,此处W是一个矩阵,用来给数据点赋予权重,这个矩阵求法如下公式:
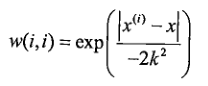
其中,x^(i)可以理解为测试样本点,x为训练集,k为用户指定参数,我们来观察一下k的影响。

很明了:
- k=1时,欠拟合,相当于普通的线性回归(所有样本点权重差不多大)
- k=0.01时,拟合的比较漂亮
- k=0.003时,过拟合(由于考虑了太多噪点)
程序:
 View Code
View Code
 View Code
View Code
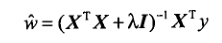
![]()
 View Code
View Code![]()
 View Code
View Code
 View Code
View Code

1 from numpy import *
2 import matplotlib.pyplot as plt
3
4 # 自适应数据加载函数
5 def loadDataSet(fileName):
6 numFeat=len(open(fileName).readline().split(' '))
7 dataMat=[];labelMat=[]
8 fr=open(fileName)
9 for line in fr.readlines():
10 lineArr=[]
11 curLine=line.strip().split(' ')
12 for i in range(numFeat-1):
13 lineArr.append(float(curLine[i]))
14 dataMat.append(lineArr)
15 labelMat.append(float(curLine[-1]))
16 return dataMat,labelMat
17
18 # 局部加权线性回归函数
19 # 给单点赋予权重
20 def lwlr(testPoint,xArr,yArr,k=0.1):
21 xMat=mat(xArr)
22 yMat=mat(yArr).T
23 m=shape(xMat)[0]
24 weights=mat(eye((m))) # 初始化权重方阵
25 for j in range(m):
26 diffMat=testPoint-xMat[j,:]
27 weights[j,j]=exp(diffMat*diffMat.T/(-2.0*k**2))
28 xTx=xMat.T*(weights*xMat)
29 if linalg.det(xTx)==0.0:
30 print("this matrix is singular,cannot do inverse")
31 return
32 ws=xTx.I*(xMat.T*(weights*yMat))
33 return testPoint*ws
34
35 # 给所有点赋予权重,并返回
36 def lwlrTest(testArr,xArr,yArr,k=1.0):
37 m=shape(testArr)[0]
38 yHat=zeros(m)
39 for i in range(m):
40 yHat[i]=lwlr(testArr[i],xArr,yArr,k)
41 return yHat
42
43 # 计算总回归误差
44 def rssError(yArr,yHatArr):
45 return ((yArr-yHatArr)**2).sum()
46
47 xArr,yArr=loadDataSet('ex1.txt')
48 xMat=mat(xArr)
49 yMat=mat(yArr)
50 yHat1=lwlrTest(xArr,xArr,yArr,1)
51 yHat01=lwlrTest(xArr,xArr,yArr,0.01)
52 yHat001=lwlrTest(xArr,xArr,yArr,0.003)
53
54 srtInd=xMat[:,1].argsort(0)
55 xSort=xMat[srtInd][:,0,:]
56 fig = plt.figure()
57 ax = fig.add_subplot(131)
58 ax.set_title('k=1')
59 ax.plot(xSort[:,1],yHat1[srtInd],color='r')
60 ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0],s=8)
61 ax = fig.add_subplot(132)
62 ax.set_title('k=0.01')
63 ax.plot(xSort[:,1],yHat01[srtInd],color='r')
64 ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0],s=8)
65 ax = fig.add_subplot(133)
66 ax.set_title('k=0.003')
67 ax.plot(xSort[:,1],yHat001[srtInd],color='r')
68 ax.scatter(xMat[:, 1].flatten().A[0], yMat.T[:, 0].flatten().A[0],s=8)
69 plt.show()
实例:预测鲍鱼的年龄。注意此处数据特征已是多维,不像之前二维,不易可视化理解。
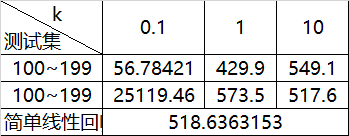
两组均是以0-99组数据作为训练集,第一组是对0-99检验拟合效果,第二组是对100-199检验拟合效果。
第一组中发现,使用较小的核可以得到较小的误差,核越小易形成过拟合,对于新数据不一定有好的预测效果
第二组中发现,核最小却是误差最大的
第三组中发现,简单线性回归与k=10时的拟合效果差不多

1 from numpy import *
2 import matplotlib.pyplot as plt
3
4 # 自适应数据加载函数
5 def loadDataSet(fileName):
6 numFeat=len(open(fileName).readline().split(' '))
7 dataMat=[];labelMat=[]
8 fr=open(fileName)
9 for line in fr.readlines():
10 lineArr=[]
11 curLine=line.strip().split(' ')
12 for i in range(numFeat-1):
13 lineArr.append(float(curLine[i]))
14 dataMat.append(lineArr)
15 labelMat.append(float(curLine[-1]))
16 return dataMat,labelMat
17
18 # 局部加权线性回归函数
19 # 给单点赋予权重
20 def lwlr(testPoint,xArr,yArr,k=0.1):
21 xMat=mat(xArr)
22 yMat=mat(yArr).T
23 m=shape(xMat)[0]
24 weights=mat(eye((m))) # 初始化权重方阵
25 for j in range(m):
26 diffMat=testPoint-xMat[j,:]
27 weights[j,j]=exp(diffMat*diffMat.T/(-2.0*k**2))
28 xTx=xMat.T*(weights*xMat)
29 if linalg.det(xTx)==0.0:
30 print("this matrix is singular,cannot do inverse")
31 return
32 ws=xTx.I*(xMat.T*(weights*yMat))
33 return testPoint*ws
34
35 # 给所有点赋予权重,并返回
36 def lwlrTest(testArr,xArr,yArr,k=1.0):
37 m=shape(testArr)[0]
38 yHat=zeros(m)
39 for i in range(m):
40 yHat[i]=lwlr(testArr[i],xArr,yArr,k)
41 return yHat
42
43 # 计算总回归误差
44 def rssError(yArr,yHatArr):
45 return ((yArr-yHatArr)**2).sum()
46
47 abX,abY=loadDataSet('abalone.txt')
48 yHat01=lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1)
49 yHat1=lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
50 yHat10=lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
51 rssError01=rssError(abY[0:99],yHat01.T)
52 rssError1=rssError(abY[0:99],yHat1.T)
53 rssError10=rssError(abY[0:99],yHat10.T)
54 print(rssError01,rssError1,rssError10)
55
56 yHat_01=lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1)
57 yHat_1=lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
58 yHat_10=lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
59 rssError_01=rssError(abY[100:199],yHat_01.T)
60 rssError_1=rssError(abY[100:199],yHat_1.T)
61 rssError_10=rssError(abY[100:199],yHat_10.T)
62 print(rssError_01,rssError_1,rssError_10)
63
64 ws=standRegres(abX[0:99],abY[0:99])
65 yHat=mat(abX[100:199])*ws
66 rssError=rssError(abY[100:199],yHat.T.A)
67 print(rssError)
3. 解决特征多于样本问题
大多数问题都是样本量远远大于特征量,但遇到了特征量大于样本该如何?
此时计算(X^T*X) 的逆矩阵会出错,许多帅比们提出了缩减方法,其中有岭回归、lasso法、前向逐步回归、LAR、PCA回归等。
缩减法的目的是去掉不重要的参数,因此可以更好理解数据。
3.1 岭回归
回归系数变为以下:
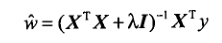
看代码:

1 from numpy import *
2 import matplotlib.pyplot as plt
3
4 # 自适应数据加载函数
5 def loadDataSet(fileName):
6 numFeat=len(open(fileName).readline().split(' '))
7 dataMat=[];labelMat=[]
8 fr=open(fileName)
9 for line in fr.readlines():
10 lineArr=[]
11 curLine=line.strip().split(' ')
12 for i in range(numFeat-1):
13 lineArr.append(float(curLine[i]))
14 dataMat.append(lineArr)
15 labelMat.append(float(curLine[-1]))
16 return dataMat,labelMat
17
18 # 岭回归
19 # 计算回归系数
20 def ridgeRegres(xMat,yMat,lam=0.2):
21 xTx=xMat.T*xMat
22 denom=xTx+eye(shape(xMat)[1])*lam
23 if linalg.det(denom)==0.0:
24 print("this matrix is singular,cannot do inverse")
25 return
26 ws=denom.I*(xMat.T*yMat)
27 return ws
28
29 # 在一组lambda上测试效果
30 def ridgeTest(xArr,yArr):
31 xMat=mat(xArr)
32 yMat=mat(yArr).T
33 yMean=mean(yMat,0)
34 yMat=yMat-yMean
35 xMeans=mean(xMat,0)
36 xVar=var(xMat,0)
37 xMat=(xMat-xMeans)/xVar
38 numTestPts=30
39 wMat=zeros((numTestPts,shape(xMat)[1]))
40 for i in range(numTestPts):
41 ws=ridgeRegres(xMat,yMat,exp(i-10))
42 wMat[i,:]=ws.T
43 return wMat
44
45 abX,abY=loadDataSet('abalone.txt')
46 ridgeWeights=ridgeTest(abX,abY)
47 fig=plt.figure()
48 ax=fig.add_subplot(111)
49 ax.plot(ridgeWeights)
50 plt.show()
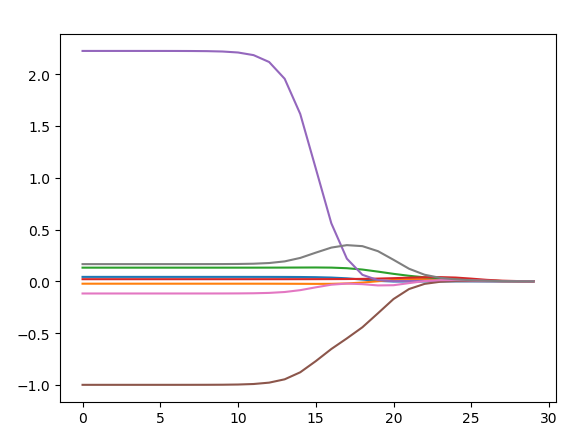
横坐标为lamda值,数座标为回归系数
岭回归的主要参数便是lambda,lambda最小时,系数与原始线性回归一致,lambda最大时,回归系数缩减为0,喇叭口处的lamda值结果预测最好。
3.2 前向逐步回归
属于一种贪心算法,即每一步都尽可能减小误差。一开始,所有的权重都设为1,然后每一步所做的决策就是对某个权重增加或者减少一个很小的值。
代码:

1 def stageWise(xArr,yArr,eps=0.01,numIt=100): 2 # 初始化 3 xMat = mat(xArr); yMat=mat(yArr).T 4 yMean = mean(yMat,0) 5 yMat = yMat - yMean 6 xMat = regularize(xMat) #特征值按均值为0方差为1进行标准化处理 7 m,n=shape(xMat) 8 returnMat = zeros((numIt,n)) 9 ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy() 10 # 迭代numIt次 11 for i in range(numIt): 12 # print(ws.T) 13 #初始误差值设置为正无穷,eps为误差增量 14 lowestError = inf; 15 for j in range(n): 16 # 分别计算增加或减少该特征对误差的影响 17 for sign in [-1,1]: 18 wsTest = ws.copy() 19 wsTest[j] += eps*sign 20 yTest = xMat*wsTest 21 rssE = rssError(yMat.A,yTest.A) 22 if rssE < lowestError: 23 lowestError = rssE 24 wsMax = wsTest 25 ws = wsMax.copy() 26 returnMat[i,:]=ws.T 27 return returnMat
4.实例:乐高玩具价格预测
代码:

1 from numpy import *
2 import matplotlib.pyplot as plt
3
4 # 计算普通线性回归,回归系数最优解
5 def standRegres(xArr,yArr):
6 xMat=mat(xArr)
7 yMat=mat(yArr).T
8 xTx=xMat.T*xMat
9 if linalg.det(xTx)==0.0:
10 print("this matrix is singular,cannot do inverse")
11 return
12 ws=xTx.I*(xMat.T*yMat)
13 return ws
14
15 # 岭回归
16 # 计算回归系数
17 def ridgeRegres(xMat,yMat,lam=0.2):
18 xTx=xMat.T*xMat
19 denom=xTx+eye(shape(xMat)[1])*lam
20 if linalg.det(denom)==0.0:
21 print("this matrix is singular,cannot do inverse")
22 return
23 ws=denom.I*(xMat.T*yMat)
24 return ws
25 # 在一组lambda上测试效果
26 def ridgeTest(xArr,yArr):
27 xMat=mat(xArr)
28 yMat=mat(yArr).T
29 yMean=mean(yMat,0)
30 yMat=yMat-yMean
31 xMeans=mean(xMat,0)
32 xVar=var(xMat,0)
33 xMat=(xMat-xMeans)/xVar
34 numTestPts=30
35 wMat=zeros((numTestPts,shape(xMat)[1]))
36 for i in range(numTestPts):
37 ws=ridgeRegres(xMat,yMat,exp(i-10))
38 wMat[i,:]=ws.T
39 return wMat
40
41 # 2.交叉验证岭回归
42 def crossValidation(xArr,yArr,numVal=10):
43 m=len(yArr)
44 indexList=list(range(m)) # 创建一组包含0-76的顺序列表
45 errorMat=zeros((numVal,30)) # 用于存放错误率的矩阵
46 # 10折交叉验证
47 for i in range(numVal):
48 trainX=[]
49 trainY=[]
50 testX=[]
51 testY=[]
52 # 打乱列表,以使每一折的训练集和测试集都不一样
53 random.shuffle(indexList)
54 # 分配训练集和测试集,前90%放入训练集,后10%放入测试集
55 for j in range(m):
56 if j<m*0.9:
57 trainX.append(xArr[indexList[j]])
58 trainY.append(yArr[indexList[j]])
59 else:
60 testX.append(xArr[indexList[j]])
61 testY.append(yArr[indexList[j]])
62 # 使用岭回归得到回归系数矩阵,用了30个lambda创建了三十组回归系数
63 wMat=ridgeTest(trainX,trainY)
64 for k in range(30):
65 matTestX=mat(testX)
66 matTrainX=mat(trainX)
67 meanTrain=mean(matTrainX,0)
68 varTrain=var(matTrainX,0)
69 # 测试集使用与训练集相同的参数进行标准化
70 matTestX=(matTestX-meanTrain)/varTrain
71 # 预测测试集的价格
72 yEst=matTestX*mat(wMat[k,:]).T+mean(trainY)
73 # 计算预测偏差
74 errorMat[i,k]=rssError(yEst.T.A,array(testY))
75 # 对各列求平均值
76 meanErrors=mean(errorMat,0)
77 minMean = float(min(meanErrors))
78 # nonzero 返回不为0元素下标
79 # 平均误差最小的组的回归系数即为所求最佳
80 bestWeights = wMat[nonzero(meanErrors == minMean)]
81 xMat = mat(xArr);
82 yMat = mat(yArr).T
83 meanX = mean(xMat, 0);
84 varX = var(xMat, 0)
85 # 数据还原标准化以前
86 unReg = bestWeights / varX
87 constant = -1 * sum(multiply(meanX, unReg)) + mean(yMat) # 常数项
88 print("the best model from Ridge Regression is:
", unReg)
89 print("with constant term: ", constant)
90 return unReg, constant
91
92 # 1.乐高玩具,数据依次是年份,零部件数,新旧,原始价格
93 xArr,yArr = loadDataSet("legoAllData.txt")
94 xMat=mat(xArr)
95 lgX=xMat
96 yMat=mat(yArr)
97 lgX1=mat(ones((76,5)))
98 lgX1[:,1:5]=xMat
99 lgY=yMat
100
101 # 2.普通线性回归
102 ws=standRegres(lgX1,lgY)
103 print(ws)
104 # 售价约等于=59349-29*年份-.0.03*零部件数+55*新旧+2*原始价格
105
106 # 3.交叉验证岭回归
107 crossValidation(xArr,yArr,10)
