机器学习实战 11- SVD

1 SVD 相关理论

1.1 奇异值分解定义

SVD,即奇异值分解，矩阵论中学过内容，公式为：

用一张图来形象表达一下：

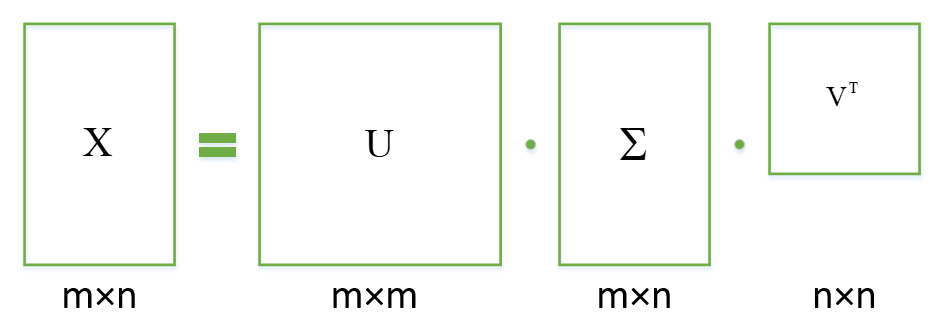
其中的奇异值矩阵，奇异值从大到小排列，而且减少的特别快，我们可以用前面最大的k个奇异值来表示这个原有矩阵，且保留大部分信息。如图：

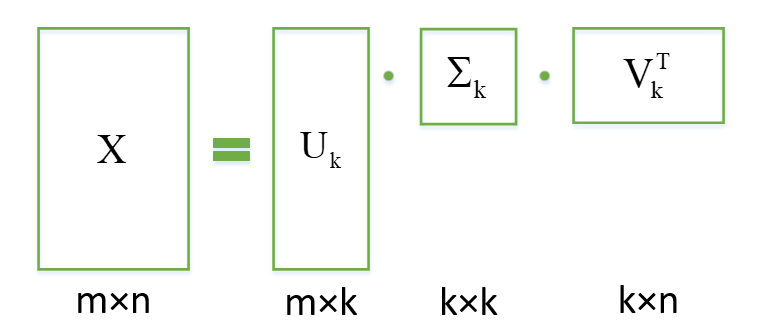
1.2 与PCA有何勾结

之前我们解释过 PCA ，PCA 的本质就是将原数据投影到低维坐标系中，获取主要信息值，起到降维作用。

究竟 SVD 与其有何关系呢？我们看一下下面的公式推导，就明白了。

由上图可以比较出，PCA 中得到的 P 就是奇异值分解中的 V。

如果需要给列降维到 k ，则：

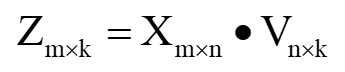
如果需要给行降维到 k ，则：

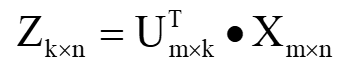
即左奇异矩阵负责给行降维，一般用来减小无效样本。

   右奇异矩阵负责给列降维，一般用来缩减特征。

1.3 优点与用途

优点：

当我们使用PCA的时候，用到协方差矩阵，但是当样本数量m大特征n也大的时候，协方差就不好计算，特征值和特征向量就不易求出。此时如果使用SVD，速度快很多，有人会说，奇异值分解时不也是利用了协方差矩阵么？其实不然这只是求取分解的一种方法，一般会使用迭代的办法，这里不赘述，只需明白它的计算速度远远加快，有兴趣可以看看这两篇文章：

并行计算奇异值：https://www.cnblogs.com/zhangchaoyang/articles/2575948.html

一篇关于奇异值计算的论文：http://www.cs.utexas.edu/users/inderjit/public_papers/HLA_SVD.pdf

　　用途：

1. 1. 特征降维

   2. 去除噪声

   3. 推荐系统

   4. 信息搜索（潜在语义分析,LSA）

2 Python 实例

2.1 基于 SVD 的图像压缩

from numpy import *
from numpy import linalg as la

def printMat(inMat,thresh=0.8):
    for i in range(32):
        for k in range(32):
            if float(inMat[i,k])>thresh:
                # pycharm中会自动换行，此处加上 end=‘’ ，以达到效果
                print('1',end='')
            else:
                print('0',end='')
        print('')

def imgCompress(numSV=3,thresh=0.8):
    my1=[]
    for line in open('0_5.txt').readlines():
        newRow=[]
        for i in range(32):
            newRow.append(int(line[i]))
        my1.append(newRow)
    myMat=mat(my1)
    print(myMat)
    print("***** original matrix *****")
    printMat(myMat,thresh)
    U,Sigma,VT=la.svd(myMat)
    SigRecon=mat(zeros((numSV,numSV)))
    for k in range(numSV):
        SigRecon[k,k]=Sigma[k]
    reconMat=U[:,:numSV]*SigRecon*VT[:numSV,:]
    print("***** reconstructed matrix using %d singular values *****")
    printMat(reconMat,thresh)

imgCompress(2)

分析：

1. 1. 左边原始矩阵，右边是奇异值分解后处理矩阵，得到的图像基本一致，可以看到只需要两个奇异值就能相对准确地对图像重建。
   2. 内存使用：原始图像：32*32=1024，奇异值分解后：2*32+2+2*32=130，缩小了将近10倍。

2.2 餐馆菜肴推荐引擎

过程：

1. 1. 寻找用户没有评级的菜肴，即在用户-物品矩阵中的 0 值。
   2. 在用户没有评级的所有物品中，对每个物品预计一个可能的评级的分数。（利用相似度进行计算）
   3. 对这些物品的评分从高到低排序，返回前 N 个物品。

程序:

from numpy import *
from numpy import linalg as la
import matplotlib.pyplot as plt

# 1. 输入数据，用户-物品评级矩阵
def loadExData2():
    return [[2, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5],
            [0, 0, 0, 0, 0, 0, 0, 1, 0, 4, 0],
            [3, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0],
            [5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0],
            [0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
            [4, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5],
            [0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4],
            [0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
            [0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0],
            [1, 1, 2, 1, 1, 2, 1, 0, 4, 5, 0]]

# 2. 几种计算相似度的方法，
# 欧式距离
def ecludSim(inA,inB):
    return 1.0/(1.0+la.norm(inA-inB))
# 皮尔逊距离
def pearsSim(inA,inB):
    if len(inA)<3:
        return 1.0
    return 0.5+0.5*corrcoef(inA,inB,rowvar=0)[0][1]
# 余弦距离
def cosSim(inA,inB):
    num =float(inA.T*inB)
    denom=la.norm(inA)*la.norm(inB)
    return 0.5+0.5*(num/denom)

# 3. 计算给定相似度计算方法下的估计评分值
# 指定用户 user 给未评定物品 item 评分
def standEst(dataMat,user,simMeas,item):
    n=shape(dataMat)[1]
    simTotal=0.0
    ratSimTotal=0.0
    # 遍历每一个物品，根每一个有过评分的物品比较，计算相似度，推测出评分
    for j in range(n):
        userRating=dataMat[user,j]
        # 如果某个用户没有对这个物品评分，跳过这个值
        if userRating==0:
            continue
        # 比较目标物品和已被评分过的物品重合程度
        overLap=nonzero(logical_and(dataMat[:,item].A>0,dataMat[:,j].A>0))[0]
        # 如果重合为0，则相似度为0
        if len(overLap)==0:
            similarity=0
        else:
            # 如果有重合，基于这些特征重合计算相似度
            similarity=simMeas(dataMat[overLap,item],dataMat[overLap,j])
            # print("the %d and %d similarity is: %f "%(item,j,similarity))
        # 累加相似度
        simTotal+=similarity
        # 累加相似度和评分的乘积，可以得到评分总和，（归一化的）
        ratSimTotal+=similarity*userRating
    if simTotal==0:
        return 0
    else:
        return ratSimTotal/simTotal

# 4. 使用 SVD 降维后进行相似度计算
def svdEst(dataMat,user,simMeas,item):
    n=shape(dataMat)[1]
    simTotal=0.0
    ratSimTotal=0.0
    U, Sigma, VT = la.svd(dataMat)
    # 取 sigma 前4的值，构建对角矩阵
    Sig4=mat(eye(4)*Sigma[:4])
    # 将原数据投影到左奇异矩阵上，使其行降维，即减少无效用户
    xformedItems=dataMat.T*U[:,:4]*Sig4.I
    for j in range(n):
        userRating=dataMat[user,j]
        if userRating==0 or j==item:
            continue
        similarity=simMeas(xformedItems[item,:].T,xformedItems[j,:].T)
        # print("the %d and %d similarity is: %f "%(item,j,similarity))
        simTotal += similarity
        # 累加相似度和评分的乘积，可以得到评分总和，（归一化的）
        ratSimTotal += similarity * userRating
    if simTotal == 0:
        return 0
    else:
        return ratSimTotal / simTotal

# 5. 推荐引擎，返回得分较高的前 N 个物品
def recommend(dataMat,user,N=3,simMeas=cosSim,estMethod=standEst):
    # 寻找未评级的物品
    unratedItems=nonzero(dataMat[user,:].A==0)[1]
    if len(unratedItems)==0:
        return print("you rated everything")
    itemScores=[]
    for item in unratedItems:
        estimatedScore=estMethod(dataMat,user,simMeas,item)
        itemScores.append((item,estimatedScore))
    return sorted(itemScores,key=lambda jj:jj[1],reverse=True)[:N]

myMat=mat(loadExData2())
print(recommend(myMat,1,estMethod=svdEst))
print(recommend(myMat,1))
U,Sigma,VT=linalg.svd(myMat)
Sig2=Sigma**2
fig=plt.figure()
ax=fig.add_subplot(111)
ax.pie(Sig2,autopct='%1.1f')
plt.show()

结果：

 

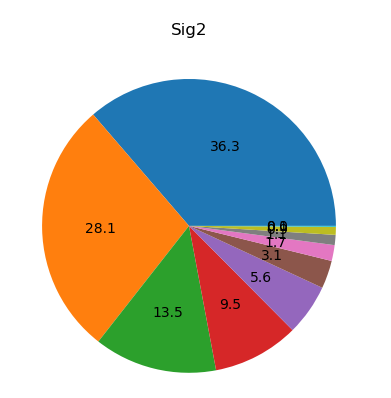
分析：

1. 对奇异值分析可知，前五个值占了绝大部分信息（注意这里与书里有些不一致）
2. 使用SVD分解后的数据推荐引擎更准确

提高构建推荐引擎时的效率：

1. SVD 大量数据分解速度慢，尽量运行一次或者离线运行。
2. 零元素太多，通过储存非零元素节省资源。
3. 每次需要推荐一个得分时，都需要计算多个物品的相似度，离线计算并保存相似度。
4. 冷启动问题：如何在缺乏数据时给出好的推荐。将推荐看成搜索问题。

参考文献：

1. 奇异值分解与在降维中的应用    https://www.cnblogs.com/pinard/p/6251584.html