Localization

Localization (using Histogram Filters)

       定位指的是在传感器和移动之间来回的迭代，使得能够保持跟踪目标对象的位置、方向和速度。

       这篇将写一个程序来实施定位，与GPS相比，这个的程序将极大的降低误差范围。

       假设一个汽车或者机器人所处在一个一维世界，它在没有得到任何提示在哪一位置。通过一个函数对这个问题建模，纵轴表概率，横轴表这个一维世界里所有位置，利用一个当值函数给这个一维世界每一个地方分配相同权重。

      

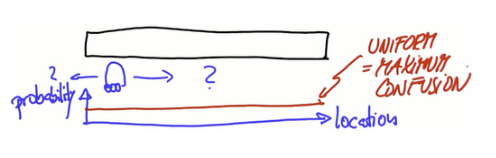
       为了定位必须引入其他特征，假设有三个看起来相似的门，可以从非门区域 区分一扇门，（brlief  = 信度），机器人感受到了它在一扇门的旁边，它分配这些地点更大的概率。门的度量改变了信度函数，得到新函数像这样，三个临近门的位置信度递加，其他所有地方信度递减，posterior bilief 表示它是在机器人进行感测测量后定义的。

                                                             

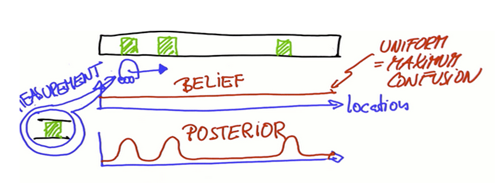
        如果机器人移动了，那么凸起的信度也会随之移动（所在位置的概率），而且凸起会因为机器人只是粗略地知道移动了多远而变得扁平化，这个过程叫卷积，卷积就是两个函数或措施的重叠，具体的说是一个函数划过另一个函数的重叠占比，介于0~1之间（CONVOLUTION 卷积）

                                                          

       假设汽车或机器人发现它的右边再一次靠近一扇门，此时在先于第二次测量的信度上乘以一个函数，函数如下，它在每一扇门下都有一个很小的凸起，但却有一个非常大的凸起。在先验上这是唯一一个真的很符合这个门的位置，所以其他的门有一个很低的信度，Posterior  belief 先验信度

                                                         

      重要的是仍然不能确定我们的位置，但是之后，会比一次或零次测量之后的测量更确定。 你认为在做了越来越多的测量后会发生什么？

                                                             

      这种定位称为Monte Carlo 定位，也称为直方图滤镜。

---

 

用Python程序化

sense( )

---

 

       新建一个列表，在这个一维世界中，假设有5个不同的单元或者说地方，用X1~X5标识，机器人落在每个单元的概率相同，概率的和加起来是1，P(Xi)表示落在其中任何一个单元格的概率。

#初始化向量
P = [0.2,0.2,0.2,0.2,0.2]
#创造一个长度为n的向量，可以通过变化n的值得到n个元素的向量
P =[ ]
n = ?

for i in range(n)
     p.append(1./n) 
print p  

       有着5个单元格的一维世界的度量方式，假设有两个被染成红色，其他两个是绿色，分配给每一个单元的概率是0.2，现在机器人允许被感知，它先看到胡是红色，23的概率会上升，145的概率会下降，用乘法将这个度量合并到信度里。

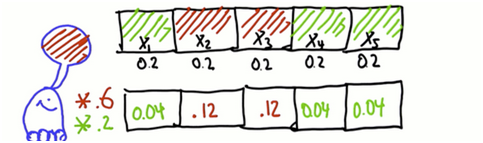
      可是这并不是一个有效的概率分布，因为概率加起来总要等于1。这些概率值的求和是0.36，为了变成有效的概率分布，把每个数除以0.36

       

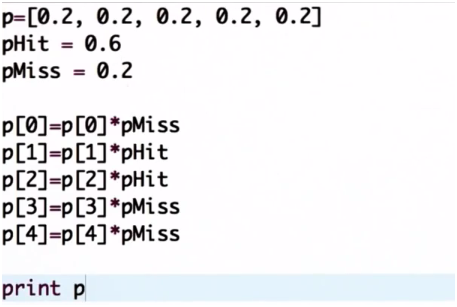
         通过引入一个变量使代码更加优雅，这个变量为每个小格指定红色或者绿色。

       此外，先前说道机器人感觉到它在一个红色的区间里，所以这里定义测量到的值为红色。

       然后，写一个叫sense的函数用在后面的定位器，它能对探测数据进行更新，输入初始分布p、探测值Z以及其他所有的全局变量，输出一个标准化分布q，q反应了输入概率的非标准化乘积

P = [0.2,0.2,0.2,0.2,0.2]
world = ['green','red','red','green','green']

#定义测量值为红色
Z = 'red'                                          

pHit = 0.6
pMiss = 0. 2

def sense()
    q = [ ]
    for i in range(len(p)):
        #用了一个二元标记，hit =0或1
        hit = (Z == world[i])                   
        #由于hit取0或1，所以每次只有一个算式成立
        q.append[p[i]*(hit*pHit+(1-hit)*pMiss)] 
    #以下代码使输出标准化（和等于1）
    s = sum(q)                                 
    for i in range(len(p))：
        q[i] = q[i] / s
    return q

    print sense(p,z)

修改代码，通过用包含多个测量值的测量值向量替代Z

假设机器人感觉到红色，之后是绿色，修改代码使得更新两次概率，并在两次测量结合后给出后验分布，以便可以处理任何测量顺序，无论长度如何。

p = [0.2, 0.2, 0.2, 0.2, 0.2]
world = ['green', 'red', 'red', 'green', 'green'] 
#替代Z
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
def sense(p, Z):
    q = [ ]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1­hit) * pMiss))
    s = sum(q)
    for i in range (len(p)):
        q[i] = q[i]/s
    return q
#抓取测试值向量中元素用来更新自己的概率
for k in range(len(measurements)): 
    p = sense(p, measurements [k])
    print p 

这个sense()就是定位中的关键函数——测量更新函数，对每个测量值调用一次这个函数并且更新概率分布

 move( )

---

假设世界是循环的，空间的概率分布如下，并且知道机器人向右移动，若机器人向右移动一个位置，运动后的后验概率分布是多少？

定义move函数，输入初始分布p和运动量U，其中U是向右或向左移动的网格的数量，返回新分布q，如果U=0，q=p

将网格2的概率从0变为1，使得向右移动一格后，以观察到运动的效果

def move(p,U)
      q = []
      for i in range(len(p))
          q.append(p[(i - U) % len(p)]) #a very skilled code
      renturn q
for k in range(len(measurements)):
    p = sense(p, measurements [k])
    print move (p, 1）

 

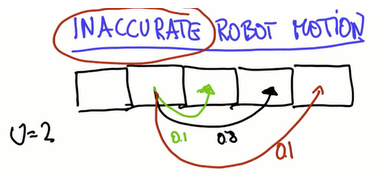
机器人移动不是准确的，定位困难

需要建立更精确的机器人运动模型，假设机器人移动到目标地的概率是0.8，到目标地之前概率是0.1，超过目标概率是0.1。

已有初始分布，给出移动后的分布

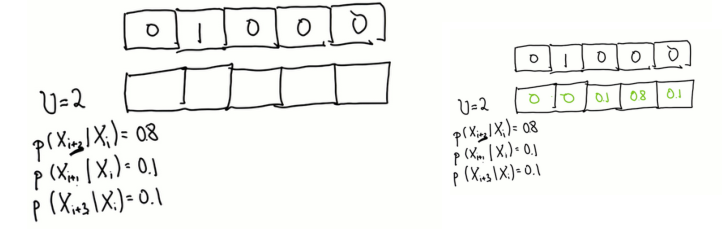
 如预期，概率分布已经转移和扩展。 移动导致信息丢失。

 

又一次，假设网格2和4的值为0.5，填充后验分布（也考虑了未达到和超过两种情况）。

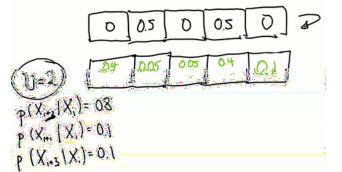
再一次，给定均匀分布，填写移动后分布。

明确计算到达每格可能方式太复杂，换种思路，如果从统一的先前分配（最大混淆状态）开始，之后移动，必定最终得到均匀分布

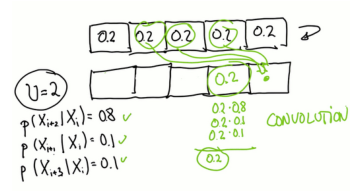
p = [0, 1, 0, 0, 0)
world = ['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
pHit = 0.6
pMiss = 0.2
#Add exact probability
pExact = 0.8
#Add overshoot/undershoot probability
pOvershoot = 0.1
pUndershoot = 0.1

def move(p, U):
    #Introduce auxiliary variable s
    q= []
    for i in range(len(p)):
        s = pExact * p[(i­U) % len(p)]
        s = s + pOvershoot * p[(i-­U­-1) % len(p)]
        s = s + pUndershoot * p[(i­-U+1) % len(p)]
        q.append(s)
    return q

该函数适应了预期的低估或超调的可能性，通过遍历p中的每个网格并且在q中的三个单元上（目标网格，距离U以及过冲和下冲网格）适当地分配其概率来移动目的地。

 

从初始分布p = [0, 1, 0, 0, 0]开始,移动两次:

p = move(p, 1)
p = move(p, 1)
print p
>>>[0.01, 0.01, 0.16, 0.66, 0.16]

结果是一个向量，其中0.66是最大值，而不是0.8。 这是预期的：两次移动已经平坦化，扩大了分布。

而后编写移动一千步后得到的概率分布：

for k in range(1000):
    p = move(p, 1)
    print p
    #最终分布是如预期的每个网格0.2

 

机器人感知和移动

---

定位，特别是这里用到的Monte Carlo定位方法，只不过是传感器和移动的迭代，有一个初始的感知抛给循环。每次移动都会丢失信息（因为机器人的移动是不准确的），每次感知会获取信息，事实证明机器人移动之后概率会变得平展、延伸，感知之后会变得更加集中。 熵是衡量分布信息的度量。

                                                                

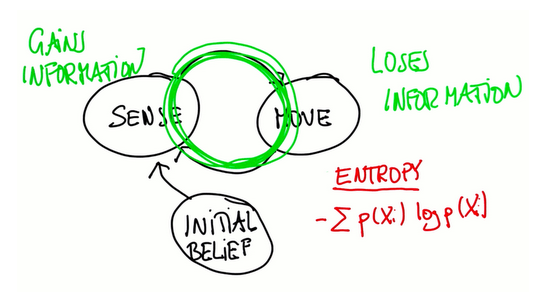
机器人从均匀的的先前分部开始，再向右移动两次，首先感觉到是红色，然后感觉到是绿色， 计算后验分布

motions = [1, 1]
p = [0.2, 0.2, 0.2, 0.2, 0.2]
for k in range(len(measurements)):
    p = sense(p, measurements[k])
    p = move(p, motions[k])
    print p

查看结果概率分布，机器人最可能是从网格3出发

如果机器人感知到两次红色

p=[0.2, 0.2, 0.2, 0.2, 0.2]
world=['green', 'red', 'red', 'green', 'green']
measurements = ['red', 'green']
motions = [1,1]
pHit = 0.6
pMiss = 0.2
pExact = 0.8
pOvershoot = 0.1
pUndershoot = 0.1

def sense(p, Z):
    q=[]
    for i in range(len(p)):
        hit = (Z == world[i])
        q.append(p[i] * (hit * pHit + (1-hit) * pMiss))
    s = sum(q)
    for i in range(len(q)):
        q[i] = q[i] / s
    return q

def move(p, U):
    q = []
    for i in range(len(p)):
        s = pExact * p[(i-U) % len(p)]
        s = s + pOvershoot * p[(i-U-1) % len(p)]
        s = s + pUndershoot * p[(i-U+1) % len(p)]
        q.append(s)
    return q

for k in range(len(measurements)):
    p = sense(p, measurements[k])
    p = move(p, motions[k])
    
print p     

结果表明机器人在网格4的概率大，也就是从网格2出发

这个代码就是Google自动驾驶定位代码的本质，也是精髓，特别重要的是，汽车准确知道它在哪里，对于它行驶的道路地图而言，虽然道路不能被涂成绿色或红色，但是道路有着路标代替红色绿色的格子，不仅是每一步一次的观察，而是整个场地的观察，整个照相机图片的观察，可以对照片做同样的事，只要能够将照片嵌入到模型当中，用在度量当中，也不会比这个代码难上多少代码，而Google花费这么多时间构建自动驾驶产品因为现实情况会很复杂，道路会正在铺设和重修，这些问题要处理。

定位总结

---

定位涉及机器人不断更新其对所有可能位置的感知。 在数学上说，可以说机器人不断更新其在样本空间上的概率分布。 对于一辆真正的自驾车，这意味着道路上的所有位置都有一个概率。

如果AI正常工作，这种概率分布应该有两个特征：

1. 应该有一个尖峰。 这表明汽车对其当前位置有非常明确的感知。
2. 峰值应该是正确的。

Monte Carlo定位程序可以写成一系列步骤：

1. 从当前位置的感知开始
2. 通过感知测量结果乘以这个分布
3. 归一化所得到的分布
4. 通过执行卷积移动。 这听起来比真的更复杂：这个步骤实则涉及乘法和加法，以获得每个新的概率位置。

 两个数学方法

---

贝叶斯法则

在概率上，经常想在更新概率分布后测量。 有时这不容易直接做。

贝叶斯法则是进行测量后更新概率分布的工具。x是网格，Z是感知度量，贝叶斯法则方程式如下：

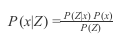
左边应该被读成“观察Z后的X的概率”，P(x)是先验分布，然后与P(Z|x)测量概率相乘，对于每个格子，可以放上下标i，P(Z)是每个格子如此操作后的和

一个用贝叶斯做癌症测试例子

全概率定理

上面是测量，再看移动，在这里要关注一个网格“xi”，并且询问机器人运动后在xi中的概率是什么。 现在，使用时间索引来表示运动前后：

P(Xi | Xj)是可从j到i的所有路径概率，利用这个定理在移动前就能算出概率分布

举个例子，抛一枚硬币，反面什么也不做。正面再抛一次，求第二次抛出正面概率

编写一个程序：

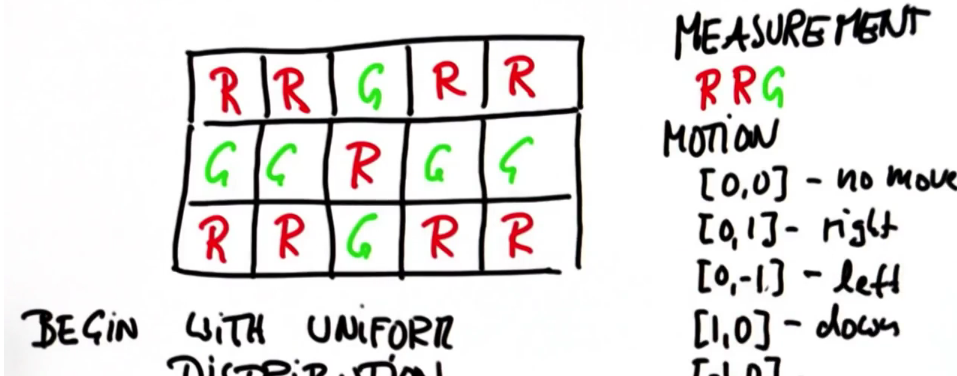
# 定位函数用到了以下参数:
# colors:
#       2D 列表, 'R' (红色网格l) or 'G' (绿色网格)
# measurements:
#       机器人得到的测量值列表 ，'R' or 'G'
# motions:
#       机器人采取的动作列表，[dy，dx]，dx表示x方向的变化（正向右移动），dy表  # 示y方向的变化（正向下移动）
#
# sensor_right:
#       测量是正确的概率，浮动在0和1之间，不正确的概率是1-sensor_right
# p_move:
#       执行移动命令的概率，浮动在0和1之间，运动命令失败的概率（仍保持原地）是
# 1-p_move; 机器人在本编程中不会超过目的地；
#
# 输出：函数返回与颜色列表尺寸相同的2D概率分布列表，最初是均匀的概率分布
#
# 每一步先行动，再测量,且任何行列是循环的

def localize(colors,measurements,motions,sensor_right,p_move):
   sensor_wrong = 1.0 - sensor_right
   p_stay = 1.0 - p_move

   if len(measurements) != len(motions)
       raise ValueError,"error in size of measurement/motion vector"

   pinit = 1.0 / float(len(colors)) / float(len(colors[0]))
   p = [[pinit for row in range(len(colors[0]))] for col in range(len(colors))]
  
   for k in range(len(measurements)):
        p = move(p,measurements[k])
        p = sense(p,colors,measurements[k])
  
   show(p)

   def sense(p,colors,measurement):
         aux = [[0.0 for row in range(len(0)) for col in range (len(p))]] 
         s = 0.0
         for i in range(len(p)):
              for j in range(len(p[i])):
                   hit = (measurement == colors[i][j])
                   aux = p[i][j]*(hit*sensor_right + (1-hit)*sensor_wrong)
                   s+=aux[i][j]
         for i in range(len(aux)):
              for j in range(len(p[i])):
                  aux[i][j] /= s
    return aux

    def move(p,motion):
          aux = [[0.0 for row in range(len(0)) for col in range (len(p))]]
          for i in range(len(p)):
               for j in range(len(p[i])):
                   aux = (p_move*p[i-motion[0] % len(p)][j - motion[1] % len(p[i])] + (p_stay*p[i][j]))
                   return aux

    def show(p):
          rows = ['[' + ','.join(map(lambda x: '{0:.5f}'.format(x),r)) + ']' for r in p]
          print '[' + ',
 '.join(rows) + ']'
    def show(p)
          for i in range(len(p))
               print p[i]


    
#############################################################
# For the following test case, your output should be 
# [[0.01105, 0.02464, 0.06799, 0.04472, 0.02465],
#  [0.00715, 0.01017, 0.08696, 0.07988, 0.00935],
#  [0.00739, 0.00894, 0.11272, 0.35350, 0.04065],
#  [0.00910, 0.00715, 0.01434, 0.04313, 0.03642]]
# (within a tolerance of +/- 0.001 for each entry)

colors = [['R','G','G','R','R'],
          ['R','R','G','R','R'],
          ['R','R','G','G','R'],
          ['R','R','R','R','R']]
measurements = ['G','G','G','G','G']
motions = [[0,0],[0,1],[1,0],[1,0],[0,1]]
p = localize(colors,measurements,motions,sensor_right = 0.7, p_move = 0.8)

 实际设计工作中怎样给这些概率赋值，例如pHit、pMiss等，从试验中获得还是传感器参数决定？

       《概率机器人》--很大程度上由传感器决定，谷歌大量使用激光雷达作为传感器，但如果选择摄像机就需要用与测距仪不同的模型，使用激光雷达时测的是距离而非pHit、pMiss，它给出的是在特定位置测得特定距离的概率。

是否要求机器人内置地图？

       yes，实时定位与地图创建SLAM

实际中的定位器是用来测什么的，显然不是一扇门？

       汽车会内置地图，激光摄像头扫描周围场景，其中包含与内置地图相同的特征，要解决的概率匹配问题是将生成的附近地图叠加到全局地图上，检查能获得最佳匹配的位置。

全工况？

       雨，调高亮度参数，雪，未解决