这两天看了看辛普森积分,觉得这是很好的骗分工具,正好也比较简单,就随便写一写。这个东西对于三次以下的函数是正确的,但是对于三次以上的函数我们可以将其近似为低次函数套用Simpson公式,这个东西学名好像叫自适应Simpson积分。
先附上公式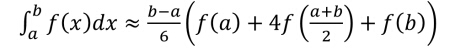 。
。
算法的大概流程就是不断的递归求对应区间的积分,当当前层和下一层的相对误差比较小时就退出,从而得到比较准确的值,但是这个其实是可以被卡掉的,比如一段波动的区间,我们取到的值有可能都是上顶点,就会直接退出,然而这并不是最后的答案。所以一般这个算法都是用来骗分的,2333。
附上代码
1 double calc(double l,double r,double fl,double fr,double fm){ 2 return (r-l)/6.0*(fl+fr+4*fm); 3 } 4 double simpson(double l,double r,double mid,double fl,double fr,double fm,double s){ 5 double m1=(l+mid)/2.0,m2=(mid+r)/2.0; 6 double f1=F(m1),f2=F(m2); 7 double s1=calc(l,mid,fl,fm,f1),s2=calc(mid,r,fm,fr,f2); 8 if(fabs(s-s1-s2)<eps)return s1+s2; 9 return simpson(l,mid,m1,fl,fm,f1,s1)+simpson(mid,r,m2,fm,fr,f2,s2); 10 }
我一般在simpson函数里会将三个函数值一并传进去,否则在单次计算f的复杂度比较大时,会重复计算,浪费时间。
hdu1724,纯板子题。
这道题我写的还是不传函数值的版本,可以对照着看看

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <cmath> 6 #define eps 1e-10 7 using namespace std; 8 double a,b; 9 int T; 10 double f(double x){ 11 return b*sqrt(1-(x*x)/(a*a)); 12 } 13 double calc(double l,double r){ 14 double mid=(l+r)/2.0; 15 return (r-l)/6*(f(l)+f(r)+4*f(mid)); 16 } 17 double simpson(double l,double r,double now){ 18 double mid=(l+r)/2.0; 19 double n1=calc(l,mid),n2=calc(mid,r); 20 if(fabs(now-n1-n2)<eps)return now; 21 return simpson(l,mid,n1)+simpson(mid,r,n2); 22 } 23 int main(){ 24 scanf("%d",&T); 25 double l,r,ans; 26 while(T--){ 27 scanf("%lf%lf%lf%lf",&a,&b,&l,&r); 28 ans=simpson(l,r,calc(l,r))*2; 29 printf("%0.3f ",ans); 30 } 31 }
bzoj2178,求圆的面积并
网上别人好像都是直接积,我是用了一个并查集,把连在一起的圆一起算,貌似这样被hack的概率比较小

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <cmath> 6 #define eps 1e-13 7 #define N 1005 8 using namespace std; 9 int v[N][N],cnt[N]; 10 int n,fa[N],del[N],tot; 11 int le[N],ri[N]; 12 int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);} 13 struct data{ 14 double s,t; 15 data(){} 16 data(double a,double b){s=a,t=b;} 17 }L[N]; 18 bool cmpdown(const data & a,const data & b){return a.s<b.s;} 19 struct cir{ 20 double x,y,r; 21 void read(){scanf("%lf%lf%lf",&x,&y,&r);} 22 }p[N],d[N]; 23 double dis(cir a,cir b){return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));} 24 bool cmpr(const cir & a,const cir & b){return a.r<b.r;} 25 bool cmpl(const int & a,const int & b){return p[a].x-p[a].r<p[b].x-p[b].r;} 26 bool check1(cir a,cir b){//包含 27 if(dis(a,b)+a.r<=b.r)return 1; 28 return 0; 29 } 30 bool check2(cir a,cir b){//相交 31 if(dis(a,b)<=a.r+b.r)return 1; 32 return 0; 33 } 34 double F(double x,int id){ 35 tot=0; 36 for(int i=1;i<=cnt[id];i++){ 37 int now=v[id][i]; 38 if(x>p[now].x+p[now].r)continue; 39 if(x<p[now].x-p[now].r)break; 40 double l=sqrt(p[now].r*p[now].r-(p[now].x-x)*(p[now].x-x)); 41 L[++tot]=data(p[now].y-l,p[now].y+l); 42 } 43 sort(L+1,L+tot+1,cmpdown); 44 double ans=0; 45 for(int i=1,j=1;i<=tot;i++){ 46 j=i;double up=L[i].t; 47 while(j<tot&&L[j+1].s<=up){j++;up=max(up,L[j].t);} 48 ans+=up-L[i].s;i=j; 49 } 50 return ans; 51 } 52 double calc(double l,double r,double fl,double fr,double fm){ 53 return (r-l)/6.0*(fl+fr+4*fm); 54 } 55 double simpson(double l,double r,double fl,double fr,double fm,double s,int id){ 56 double mid=(l+r)/2.0,m1=(l+mid)/2.0,m2=(mid+r)/2.0; 57 double f1=F(m1,id),f2=F(m2,id),s1=calc(l,mid,fl,fm,f1),s2=calc(mid,r,fm,fr,f2); 58 if(fabs(s-s1-s2)<eps)return s1+s2; 59 return simpson(l,mid,fl,fm,f1,s1,id)+simpson(mid,r,fm,fr,f2,s2,id); 60 } 61 int main(){ 62 memset(le,0x3f,sizeof le); 63 memset(ri,-0x3f,sizeof ri); 64 scanf("%d",&n); 65 for(int i=1;i<=n;i++)p[i].read(),fa[i]=i; 66 sort(p+1,p+n+1,cmpr); 67 for(int i=1;i<=n;i++) 68 for(int j=i+1;j<=n;j++)if(check1(p[i],p[j])){ 69 del[i]=1; 70 break; 71 } 72 for(int i=1;i<=n;i++)if(!del[i])d[++tot]=p[i]; 73 n=tot; 74 for(int i=1;i<=n;i++)p[i]=d[i]; 75 for(int i=1;i<=n;i++) 76 for(int j=i+1;j<=n;j++) 77 if(check2(p[i],p[j])) 78 fa[find(j)]=find(i); 79 for(int i=1;i<=n;i++){ 80 int f=find(i); 81 v[f][++cnt[f]]=i; 82 le[f]=min(le[f],(int)(p[i].x-p[i].r)); 83 ri[f]=max(ri[f],(int)(p[i].x+p[i].r)); 84 } 85 double ans=0; 86 for(int i=1;i<=n;i++){ 87 if(cnt[i]){ 88 sort(v[i]+1,v[i]+cnt[i]+1,cmpl); 89 double fl=F(le[i],i),fr=F(ri[i],i),fm=F((le[i]+ri[i])/2.0,i); 90 ans+=simpson(le[i],ri[i],fl,fr,fm,calc(le[i],ri[i],fl,fr,fm),i); 91 } 92 } 93 printf("%0.3lf ",ans); 94 return 0; 95 }
bzoj1502,转化完题面就是要求一些圆以及相邻圆公切线所包含的面积。
我被一个地方坑了一上午,最后发现是因为我先把包含的圆去掉再算的切线。身败名裂

1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <algorithm> 5 #include <cmath> 6 #define N 550 7 #define eps 1e-5 8 using namespace std; 9 int tot,n,cnt; 10 double alp; 11 struct line{ 12 double x1,x2,y1,y2,K,B; 13 bool operator < (const line & a)const{return x1<a.x1;} 14 }l[N]; 15 struct cir{ 16 double x,r; 17 }p[N],d[N]; 18 void solve(cir a,cir b){ 19 if(a.r==b.r){ 20 l[++cnt].x1=a.x;l[cnt].x2=b.x; 21 l[cnt].y1=l[cnt].y2=a.r; 22 l[cnt].K=0; 23 l[cnt].B=a.r; 24 return ; 25 } 26 if(a.r>b.r){ 27 double r1=a.r,r2=b.r,c=b.x-a.x; 28 if(r2){ 29 double d=c*r2/(r1-r2); 30 double e=sqrt(d*d-r2*r2); 31 l[++cnt].x1=a.x+r1*r2/d;l[cnt].y1=r1*e/d; 32 l[cnt].x2=b.x+r2*r2/d;l[cnt].y2=r2*e/d; 33 } 34 else{ 35 double d=sqrt(c*c-r1*r1); 36 l[++cnt].x1=a.x+r1*r1/c;l[cnt].y1=r1*d/c; 37 l[cnt].x2=b.x;l[cnt].y2=0; 38 } 39 l[cnt].K=(l[cnt].y2-l[cnt].y1)/(l[cnt].x2-l[cnt].x1); 40 l[cnt].B=(l[cnt].y1)-l[cnt].K*l[cnt].x1; 41 return ; 42 } 43 if(a.r<b.r){ 44 double r1=a.r,r2=b.r,c=b.x-a.x; 45 double d=c*r1/(r2-r1); 46 double e=sqrt(d*d-r1*r1); 47 l[++cnt].x1=a.x-r1*r1/d;l[cnt].y1=r1*e/d; 48 l[cnt].x2=b.x-r2*r1/d;l[cnt].y2=r2*e/d; 49 l[cnt].K=(l[cnt].y2-l[cnt].y1)/(l[cnt].x2-l[cnt].x1); 50 l[cnt].B=(l[cnt].y1)-l[cnt].K*l[cnt].x1; 51 return ; 52 } 53 } 54 double F(double x){ 55 double ans=0; 56 for(int i=1;i<=cnt;i++){ 57 if(x>l[i].x2)continue; 58 if(x<l[i].x1)break; 59 ans=max(ans,l[i].K*x+l[i].B); 60 } 61 for(int i=1;i<=n;i++){ 62 if(x>p[i].x+p[i].r)continue; 63 if(x<p[i].x-p[i].r)break; 64 if(!p[i].r)continue; 65 double now=(x-p[i].x); 66 ans=max(ans,sqrt(p[i].r*p[i].r-now*now)); 67 } 68 return ans*2.0; 69 } 70 double calc(double l,double r,double fl,double fr,double fm){ 71 return (r-l)/6.0*(fl+fr+4*fm); 72 } 73 double simpson(double l,double r,double mid,double fl,double fr,double fm,double s){ 74 double m1=(l+mid)/2.0,m2=(mid+r)/2.0; 75 double f1=F(m1),f2=F(m2); 76 double s1=calc(l,mid,fl,fm,f1),s2=calc(mid,r,fm,fr,f2); 77 if(fabs(s-s1-s2)<eps)return s1+s2; 78 return simpson(l,mid,m1,fl,fm,f1,s1)+simpson(mid,r,m2,fm,fr,f2,s2); 79 } 80 int del[N]; 81 double h[N],r[N],sum[N]; 82 int main(){ 83 scanf("%d%lf",&n,&alp); 84 alp=tan(alp); 85 for(int i=1;i<=n+1;i++)scanf("%lf",&h[i]),sum[i]=sum[i-1]+h[i]; 86 for(int i=1;i<=n;i++)scanf("%lf",&r[i]); 87 for(int i=1;i<=n;i++)p[i].x=sum[i]/alp,p[i].r=r[i]; 88 p[n+1].x=sum[n+1]/alp;p[n+1].r=0; 89 for(int i=1;i<=n;i++)if(fabs(p[i+1].x-p[i].x)>fabs(p[i+1].r-p[i].r)) 90 solve(p[i],p[i+1]); 91 sort(l+1,l+cnt+1); 92 for(int i=1;i<=n+1;i++) 93 for(int j=1;j<=n+1;j++)if(i!=j&&!del[j]) 94 if(fabs(p[i].x-p[j].x)+p[i].r<=p[j].r){del[i]=1;break;} 95 for(int i=1;i<=n+1;i++)if(!del[i])d[++tot]=p[i]; 96 n=tot; 97 for(int i=1;i<=n;i++)p[i]=d[i]; 98 double l=p[1].x-p[1].r,r=p[n].x+p[n].r,mid=(l+r)/2.0; 99 double fl=F(l),fr=F(r),fm=F(mid),s=calc(l,r,fl,fr,fm); 100 double ans=simpson(l,r,mid,fl,fr,fm,s); 101 printf("%0.2f ",ans); 102 return 0; 103 }
我就找到这三道水题,感觉这个也就是用来骗分,掌握了也没有什么坏处。
