交叉熵损失函数原理详解
一、总结
一句话总结:
1、叉熵损失函数(CrossEntropy Loss):分类问题中经常使用的一种损失函数
2、交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
3、交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
1、交叉熵简介?
交叉熵是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性
2、信息的实质与例子(I(x)=-log(P(x)))?
1、信息奠基人香农(Shannon)认为【“信息是用来消除随机不确定性的东西”】,也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
2、“太阳从东边升起”,这条信息并没有减少不确定性,因为太阳肯定是从东边升起的,这是一句废话,信息量为0。
3、“2018年中国队成功进入世界杯”,从直觉上来看,这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大,而这句话消除了进入世界杯的不确定性,所以按照定义,这句话的信息量很大。
4、根据上述可总结如下:信息量的大小与信息发生的概率成反比。概率越大,信息量越小。概率越小,信息量越大。
3、信息熵是什么?
a、信息熵也被称为熵,用来表示所有信息量的期望。
b、期望是试验中每次可能结果的概率乘以其结果的总和。
c、信息量的熵可表示为:Σ((-log(P(x))*P(x))
4、为什么0-1分布问题可以用信息熵?
A、对于0-1分布的问题,由于其结果只用两种情况,是或不是,设某一件事情发生的概率为P(x),则另一件事情发生的概率为1−P(x),
B、所以对于0-1分布的问题,计算熵的公式可以简化如下:(-log(P(x))*P(x) + (-log(1-P(x))*(1-P(x))
5、交叉熵在单分类问题中的应用?
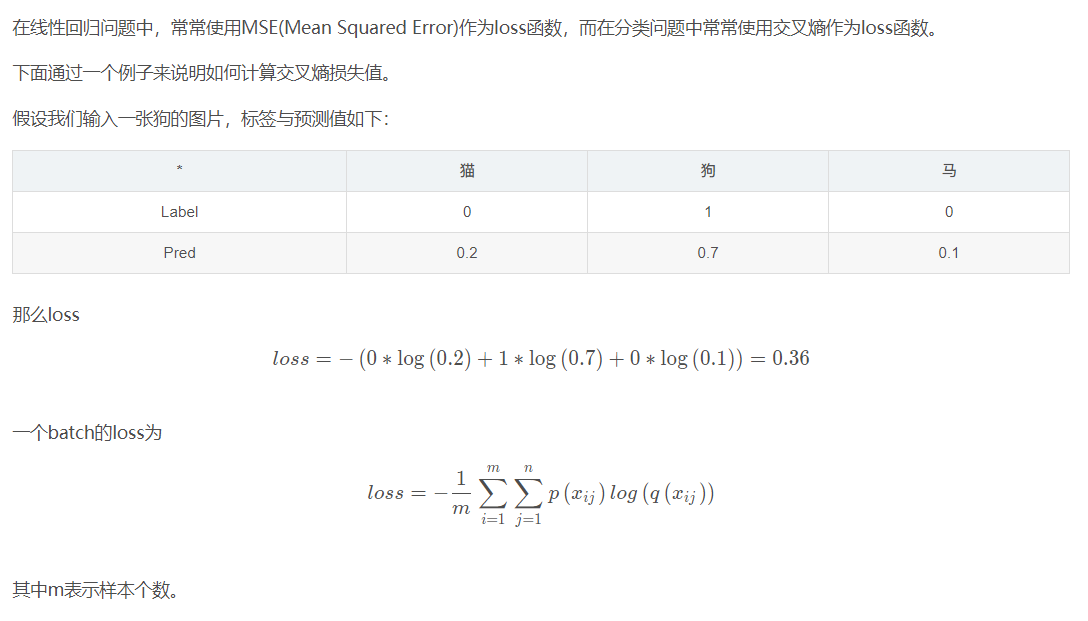
在线性回归问题中,常常使用MSE(Mean Squared Error)作为loss函数,而在分类问题中常常使用交叉熵作为loss函数。
二、交叉熵损失函数原理详解
转自或参考:交叉熵损失函数原理详解
https://blog.csdn.net/b1055077005/article/details/100152102
之前在代码中经常看见交叉熵损失函数(CrossEntropy Loss),只知道它是分类问题中经常使用的一种损失函数,对于其内部的原理总是模模糊糊,而且一般使用交叉熵作为损失函数时,在模型的输出层总会接一个softmax函数,至于为什么要怎么做也是不懂,所以专门花了一些时间打算从原理入手,搞懂它,故在此写一篇博客进行总结,以便以后翻阅。
交叉熵简介
交叉熵是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性,要理解交叉熵,需要先了解下面几个概念。
信息量
信息奠基人香农(Shannon)认为“信息是用来消除随机不确定性的东西”,也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
“太阳从东边升起”,这条信息并没有减少不确定性,因为太阳肯定是从东边升起的,这是一句废话,信息量为0。
”2018年中国队成功进入世界杯“,从直觉上来看,这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大,而这句话消除了进入世界杯的不确定性,所以按照定义,这句话的信息量很大。
根据上述可总结如下:信息量的大小与信息发生的概率成反比。概率越大,信息量越小。概率越小,信息量越大。

信息熵
信息熵也被称为熵,用来表示所有信息量的期望。
期望是试验中每次可能结果的概率乘以其结果的总和。
所以信息量的熵可表示为:(这里的XXX是一个离散型随机变量)
相对熵(KL散度)

交叉熵

交叉熵在单分类问题中的应用
总结:
-
交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
-
交叉熵在分类问题中常常与softmax是标配,softmax将输出的结果进行处理,使其多个分类的预测值和为1,再通过交叉熵来计算损失。
参考:
https://blog.csdn.net/tsyccnh/article/details/79163834