对于梯度消失和梯度爆炸的理解
一、总结
一句话总结:
梯度消失或者梯度爆炸,简单一点来讲就是层数太多,链式求梯度的时候连乘太多
1、循环神经网络梯度消失或者梯度爆炸说明?
(1)、$$W ^ { t } = ( V operatorname { diag } ( lambda ) V ^ { - 1 } ) ^ { t } = V operatorname { diag } ( lambda ) ^ { t } V ^ { - 1 }$$
(2)、若特征值大于1,则会出现梯度爆炸,若特征值小于1,则会出现梯度消失。
(3)、因此在一定程度上,RNN对比BP更容易出现梯度问题。主要是因为RNN处理时间步长一旦长了,W求导的路径也变的很长,即使RNN深度不大,也会比较深的BP神经网络的链式求导的过程长很大;
(4)、另外,对于共享权值w,不同的wi相乘也在一定程度上可以避免梯度问题。
2、如何解决梯度消失、梯度爆炸?
1、对于RNN,可以通过梯度截断,避免梯度爆炸
2、可以通过添加正则项,避免梯度爆炸
3、使用LSTM等自循环和门控制机制,避免梯度消失
4、优化激活函数,譬如将sigmold改为relu,避免梯度消失
二、对于梯度消失和梯度爆炸的理解
转自或参考:对于梯度消失和梯度爆炸的理解
https://www.cnblogs.com/pinking/p/9418280.html
一、梯度消失、梯度爆炸产生的原因
说白了,对于1.1 1.2,其实就是矩阵的高次幂导致的。在多层神经网络中,影响因素主要是权值和激活函数的偏导数。
1.1 前馈网络
假设存在一个网络结构如图:

其表达式为:
![]()
若要对于w1求梯度,根据链式求导法则,得到的解为:
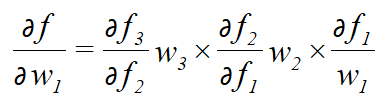
通常,若使用的激活函数为sigmoid函数,其导数:
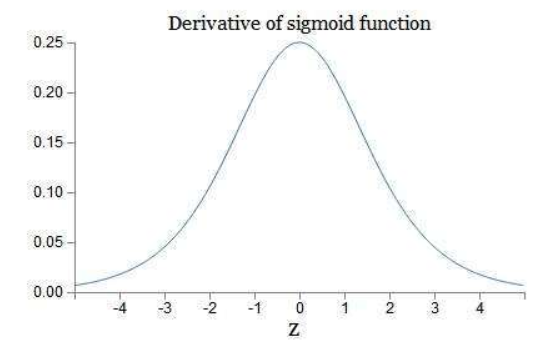
这样可以看到,如果我们使用标准化初始w,那么各个层次的相乘都是0-1之间的小数,而激活函数f的导数也是0-1之间的数,其连乘后,结果会变的很小,导致梯度消失。若我们初始化的w是很大的数,w大到乘以激活函数的导数都大于1,那么连乘后,可能会导致求导的结果很大,形成梯度爆炸。
当然,若对于b求偏导的话,其实也是一个道理:
![]()
推出:
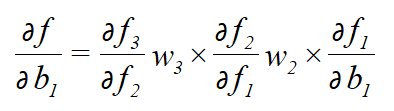
1.2 RNN
对于RNN的梯度下降方法,是一种基于时间的反向求导算法(BPTT),RNN的表达式:
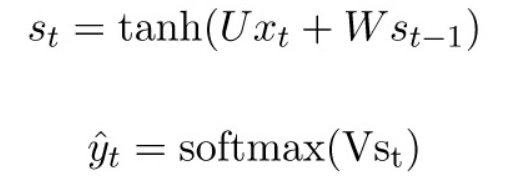
通常我们会将一个完整的句子序列视作一个训练样本,因此总误差即为各时间步(单词)的误差之和。
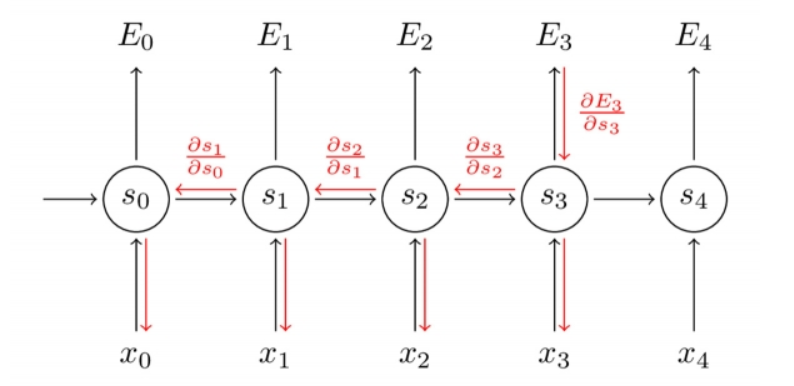
而RNN还存在一个权值共享的问题,即这几个w都是一个,假设,存在一个反复与w相乘的路径,t步后,得到向量:
![]()
若特征值大于1,则会出现梯度爆炸,若特征值小于1,则会出现梯度消失。因此在一定程度上,RNN对比BP更容易出现梯度问题。主要是因为RNN处理时间步长一旦长了,W求导的路径也变的很长,即使RNN深度不大,也会比较深的BP神经网络的链式求导的过程长很大;另外,对于共享权值w,不同的wi相乘也在一定程度上可以避免梯度问题。
1.3 悬崖和梯度爆炸
对于目标函数,通常存在梯度变化很大的一个“悬崖”,在此处求梯度,很容易导致求解不稳定的梯度爆炸现象。

三、梯度消失和梯度爆炸哪种经常出现
事实上,梯度消失更容易出现,因为对于激活函数的求导:
![]()
可以看到,当w越大,其wx+b很可能变的很大,而根据上面sigmoid函数导数的图像可以看到,wx+b越大,导数的值也会变的很小。因此,若要出现梯度爆炸,其w既要大还要保证激活函数的导数不要太小。
二、如何解决梯度消失、梯度爆炸
1、对于RNN,可以通过梯度截断,避免梯度爆炸
2、可以通过添加正则项,避免梯度爆炸
3、使用LSTM等自循环和门控制机制,避免梯度消失,参考:https://www.cnblogs.com/pinking/p/9362966.html
4、优化激活函数,譬如将sigmold改为relu,避免梯度消失