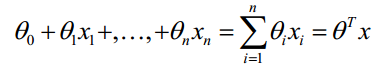多元线性回归模型

多元线性回归模型

一、总结

一句话总结：

【也就是多元且一次的回归，系数是一次自然是线性】：回归分析中，含有两个或者两个以上自变量，称为多元回归，若自变量系数为1，则此回归为多元线性回归。

1、一元线性回归 与 二元线性回归图像（要回忆图）？

一元线性回归图形为一条直线。而二元线性回归，拟合的为一个平面。

二、机器学习（多元线性回归模型&逻辑回归）

转自或参考：机器学习（多元线性回归模型&逻辑回归）
https://blog.csdn.net/weixin_44638960/article/details/104081680

多元线性回归

定义：回归分析中，含有两个或者两个以上自变量，称为多元回归，若自变量系数为1，则此回归为多元线性回归。

（特殊的：自变量个数为1个，为一元线性回归）多元线性回归模型如下所示：

如上图所示，一元线性回归图形为一条直线。而二元线性回归，拟合的为一个平面。多元线性回归拟合出的图像为以超平面；

逻辑回归（分类问题的处理）

求解步骤：1）确定回归函数 (通常用Sigmoid函数) ； 2）确定代价函数（含有参数）；3）求解参数（梯度下降/最大似然）

1）Sigmoid函数可以作为二分类问题的回归函数，而且此函数为连续的且通过0为界限分为大于0.5与小于0.5的两部分；

Sigmoid函数形式为：

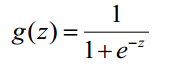
Sigmoid函数图像为：（连续可导满足我们的需求，便于后续参数的求解）

第一步：构造预测函数为：

（在这里就是将sigmoid函数中的自变量部分替换为多元线性回归模型）

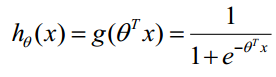
第二步：构造损失函数：

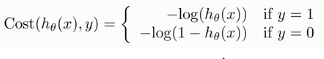
这里的y为样本的真实值，根据预测值与真实值之间的关系构造损失函数，求解预测函数参数使得其损失值最小。

结合函数图像当真实值y=1时，预测值越接近1则代价越小（反之越大），同理可得真实值y=0的情况；

由此我们根据y的取值不同构造出损失函数：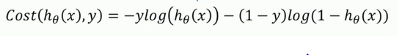

第三步：求解函数参数：在这里采用梯度下降法求解参数 ；

通过对参数求偏导数可得变化率为，并通过此关系式求解参数；

逻辑回归实战（Fight）

1）导入所需要的库文件以及获取数据集合（数据集合在最底部^_^）

import numpy as np
import matplotlib.pyplot as plt
import  math
#导入必备的包

positive = [] #正值点
negative = [] #负值点
#导入数据
dataSet = [] #数据点
def functionexp(k1,k2,x,y,b):
    return math.exp(k1 * x + k2 *y + b)  #e^(θx+b)

#数据集合获取
with open('testSet.txt') as f:
    for line in f:
        line = line.strip('
').split('	')
        if line[2]=='1':
            positive.append([float(line[0]),float(line[1])])
        else:
            negative.append([float(line[0]),float(line[1])])
        dataSet.append([float(line[0]),float(line[1]),int(line[2])])

2）根据样本集合求解参数（使用梯度下降法）

#求解参数
k1 = 0
k2 = 0
b = 0
step =2500 #学习步长
learnrate = 1 #学习率
for i in range(step):
    temp0 = 0
    temp1 = 0 #初始化参数
    temp2 = 0
    for j in dataSet:
        e = functionexp(k1, k2, j[0], j[1], b)
        temp0 = temp0 + (e /( 1 + e ) - j[2] ) / len(dataSet)
        temp1 = temp1 + (e / (1 + e ) - j[2] ) * j[0]/ len(dataSet)
        temp2 = temp2 + (e / (1 + e ) - j[2] ) * j[1] / len(dataSet)
    k1 = k1 - temp1 * learnrate
    k2 = k2 - temp2 * learnrate
    b  = b  - temp0 * learnrate

3）绘制样本散点图以及决策边界（拟合曲线）

#绘制样本点以及分类边界
dataX = []#样本点X集合
dataY = []#样本点Y集合
for i in positive:
    dataX.append(i[0])
    dataY.append(i[1])
plt.scatter(dataX,dataY,c='red')#绘制正样本散点图
dataX.clear()
dataY.clear()
for i in negative:
    dataX.append(i[0])
    dataY.append(i[1])
plt.scatter(dataX,dataY,c='blue')#绘制负样本散点图
XX=[-3,3]
plt.plot(XX,(-k1/k2)*np.array(XX)-b/k2,'yellow')
plt.show()

运行结果如下图所示（这里没有过多使用numpy库中的矩阵运算，仅限理解逻辑回归）

up通过sklearn进行逻辑回归：

import numpy as np
import matplotlib.pyplot as plt
import  math
from sklearn import linear_model
from sklearn import preprocessing
from sklearn.metrics import classification_report

positive = [] #正值点
negative = [] #负值点
#导入数据
dataSet = [] #数据点
X=[]
Y=[]

#数据集合获取
with open('testSet.txt') as f:
    for line in f:
        line = line.strip('
').split('	')
        if line[2]=='1':
            positive.append([float(line[0]),float(line[1])])
        else:
            negative.append([float(line[0]),float(line[1])])
        dataSet.append([float(line[0]),float(line[1]),int(line[2])])
        X.append([float(line[0]),float(line[1])])
        Y.append([int(line[2])])

#求解参数
logistic = linear_model.LogisticRegression()
logistic.fit(np.array(X),np.array(Y))

#绘制样本点以及分类边界
dataX = []#样本点X集合
dataY = []#样本点Y集合
for i in positive:
    dataX.append(i[0])
    dataY.append(i[1])
plt.scatter(dataX,dataY,c='red')#绘制正样本散点图
dataX.clear()
dataY.clear()
for i in negative:
    dataX.append(i[0])
    dataY.append(i[1])
plt.scatter(dataX,dataY,c='blue')#绘制负样本散点图
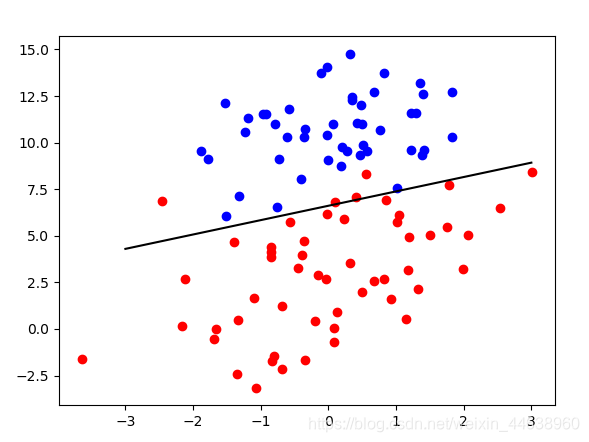
XX=[-3,3]
plt.plot(XX,(-np.array(XX)*logistic.coef_[0][0]-logistic.intercept_)/logistic.coef_[0][1],'black')
plt.show()

回归效果（感觉比自己写的回归效果好=_=）

总结 （关于逻辑回归的思考以及正确率、召回率、F1指标）

在分类问题中可以灵活运用二分类的解法来求解多分类问题（是否问题，即是这一类的和不是这一类的），将多分类问题

转化为二分类问题。而且采用的模型并不一定必须是多元线性模型（非线性模型），根据情况选取合适的模型。

正确率：检索出来的条目有多少是正确的（相对于结果而言）。即：正确的个数在预测为正确总个数的比例；

召回率：正确的有多少被检测出来了，即：检测（预测）出的正确个数/总正确个数；

F1指标：2*正确率*召回率/（正确率+召回率）；（综合反映上述两个指标）

以上的指标都是介于0-1之间的，且数值越接近于1说明效果越好；

-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
0.423363	11.054677	0
0.406704	7.067335	1
0.667394	12.741452	0
-2.460150	6.866805	1
0.569411	9.548755	0
-0.026632	10.427743	0
0.850433	6.920334	1
1.347183	13.175500	0
1.176813	3.167020	1
-1.781871	9.097953	0
-0.566606	5.749003	1
0.931635	1.589505	1
-0.024205	6.151823	1
-0.036453	2.690988	1
-0.196949	0.444165	1
1.014459	5.754399	1
1.985298	3.230619	1
-1.693453	-0.557540	1
-0.576525	11.778922	0
-0.346811	-1.678730	1
-2.124484	2.672471	1
1.217916	9.597015	0
-0.733928	9.098687	0
-3.642001	-1.618087	1
0.315985	3.523953	1
1.416614	9.619232	0
-0.386323	3.989286	1
0.556921	8.294984	1
1.224863	11.587360	0
-1.347803	-2.406051	1
1.196604	4.951851	1
0.275221	9.543647	0
0.470575	9.332488	0
-1.889567	9.542662	0
-1.527893	12.150579	0
-1.185247	11.309318	0
-0.445678	3.297303	1
1.042222	6.105155	1
-0.618787	10.320986	0
1.152083	0.548467	1
0.828534	2.676045	1
-1.237728	10.549033	0
-0.683565	-2.166125	1
0.229456	5.921938	1
-0.959885	11.555336	0
0.492911	10.993324	0
0.184992	8.721488	0
-0.355715	10.325976	0
-0.397822	8.058397	0
0.824839	13.730343	0
1.507278	5.027866	1
0.099671	6.835839	1
-0.344008	10.717485	0
1.785928	7.718645	1
-0.918801	11.560217	0
-0.364009	4.747300	1
-0.841722	4.119083	1
0.490426	1.960539	1
-0.007194	9.075792	0
0.356107	12.447863	0
0.342578	12.281162	0
-0.810823	-1.466018	1
2.530777	6.476801	1
1.296683	11.607559	0
0.475487	12.040035	0
-0.783277	11.009725	0
0.074798	11.023650	0
-1.337472	0.468339	1
-0.102781	13.763651	0
-0.147324	2.874846	1
0.518389	9.887035	0
1.015399	7.571882	0
-1.658086	-0.027255	1
1.319944	2.171228	1
2.056216	5.019981	1
-0.851633	4.375691	1
-1.510047	6.061992	0
-1.076637	-3.181888	1
1.821096	10.283990	0
3.010150	8.401766	1
-1.099458	1.688274	1
-0.834872	-1.733869	1
-0.846637	3.849075	1
1.400102	12.628781	0
1.752842	5.468166	1
0.078557	0.059736	1
0.089392	-0.715300	1
1.825662	12.693808	0
0.197445	9.744638	0
0.126117	0.922311	1
-0.679797	1.220530	1
0.677983	2.556666	1
0.761349	10.693862	0
-2.168791	0.143632	1
1.388610	9.341997	0
0.317029	14.739025	0