机器学习西瓜书笔记---2.4-2.6、模型评估与选择【2.4比较检验,2.5偏差与方差】
一、总结
一句话总结:
【学以致用】,讲到底其实【用以致学】更好
1、机器学习中性能比较涉及的几个重要因素?
【泛化性能与测试集上的性能的矛盾】:首先,我们希望比较的是【泛化性能】,然而通过实验评估方法我们获得的是【测试集上的性能】,两者的对比结果可能未必相同;
【测试集不同导致的结果不同】:第二,测试集上的性能与测试集本身的选择有很大关系,且不论使用不同大小的测试集会得到不同的结果,即便用相同大小的测试集,【若包含的测试样例不同,测试结果也会有不同】;
【机器算法的随机性】:第三,很多机器学习算法本身有一定的【随机性】,即便【用相同的参数设置在同一个测试集上多次运行,其结果也会有不同】.
【统计假设检验可以解决问题】:那么,有没有适当的方法对学习器的性能进行比较呢:【统计假设检验(hypothesis test)】为我们进行学习器性能比较提供了重要依据.
2、统计假设检验(hypothesis test)?
统计假设检验(hypothesis test)为我们进行学习器性能比较提供了重要依据.基于假设检验结果我们可推断出,【若在测试集上观察到学习器A比B好,则A的泛化性能是否在统计意义上优于B,以及这个结论的把握有多大】.
下面我们先介绍【两种最基本的假设检验】,然后介绍【几种常用的机器学习性能比较方法】.为便于讨论,本节默认以错误率为性能度量,用ε表示.
3、假设检验 的意义?
【就是判断测试集性能和真正的泛化性能】:假设检验中的“假设”是对学习器泛化错误率分布的某种判断或猜想,例如“ε=ε0”.现实任务中我们并不知道学习器的泛化错误率,只能获知其测试错误率.泛化错误率与测试错误率未必相同,但直观上,二者接近的可能性应比较大,相差很远的可能性比较小.因此,可根据测试错误率估推出泛化错误率的分布.
【假设检验没有细看】:后面可以去看概率书配合西瓜书
4、2.5偏差与方差?
对学习算法除了通过实验估计其泛化性能,人们往往还希望了解它【“为什么”具有这样的性能】.
【“偏差-方差分解”(bias-variance decomposition)】是解释学习【算法泛化性能】的一种重要工具.
5、偏差与方差 公式?
对测试样本x,令yD为x在数据集中的标记,y为x的真实标记,f(x;D)为训练集D上学得模型f在x上的预测输出.
使用样本数相同的不同训练集产生的方差为:$$operatorname { var } ( x ) = E _ { D } [ ( f ( x ; D ) - overline { f } ( x ) ) ^ { 2 } ]$$,噪声为$$varepsilon ^ { 2 } = E _ { D } [ ( y _ { D } - y ) ^ { 2 } ]$$
期望输出与真实标记的差别称为偏差(bias),即:$$operatorname { bias } ^ { 2 } ( x ) = ( overline { f } ( x ) - y ) ^ { 2 }$$
【泛化误差可分解为偏差、方差与噪声之和】:$$E ( f ; D ) = operatorname { bias } ^ { 2 } ( x ) + operatorname { var } ( x ) + varepsilon ^ { 2 }$$
6、偏差、方差、噪声的含义?
【偏差】(2.40)度量了学习算法的【期望预测与真实结果的偏离程度】,即刻画了【学习算法本身的拟合能力】;
【方差】(2.38)度量了同样大小的【训练集的变动】所导致的学习性能的变化,即刻画了【数据扰动】所造成的影响;
【噪声】(2.39)则表达了在当前任务上任何学习算法所能达到的【期望泛化误差的下界】,即刻画了【学习问题本身的难度】.
偏差-方差分解说明,【泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的】.给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小.
7、偏差-方差窘境(bias-variancedilemma)?
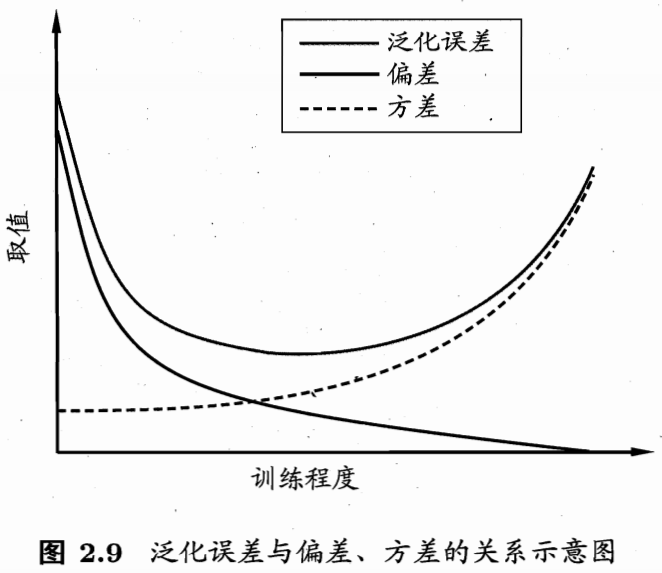
给定学习任务,假定我们能控制学习算法的训练程度,则在训练不足时,学习器的拟合能力不够强,【训练数据的扰动不足】以使学习器产生显著变化,此时【偏差】主导了泛化错误率;
随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据发生的扰动渐渐能【被学习器学】到,【方差】逐渐主导了泛化错误率;
在训练程度充足后,学习器的拟合能力已非常强,【训练数据发生的轻微扰动】都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生【过拟合】.
二、内容在总结中
博客对应课程的视频位置: