递推3--位数问题
一、心得
问题想清楚
注意边界
二、题目及分析

三、代码及结果
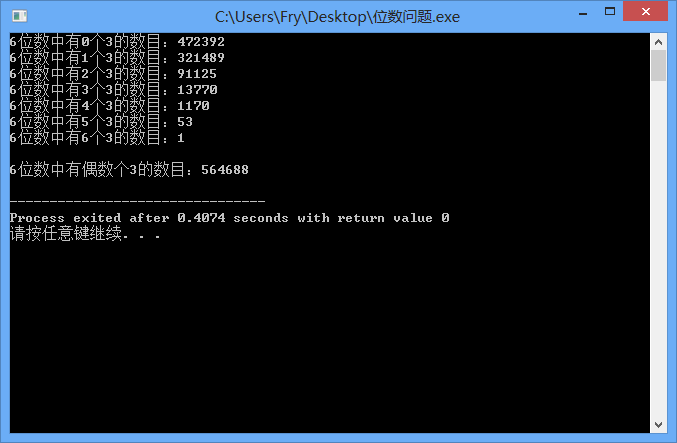
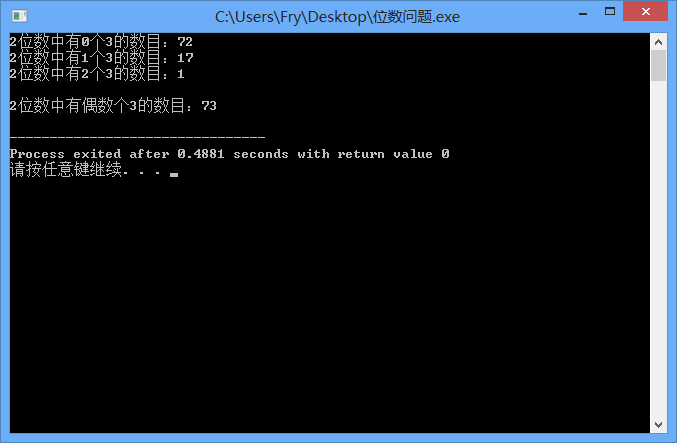
方法一:排列组合
1 /* 2 位数问题 : 3 在所有的n位数中,有多少个数中有偶数个数字3? 4 5 方法一: 6 排列组合 7 n位数中有x个三的情况为:c(n,x)*9^(n-x) 8 还要减去首位为0的情况:c(n-1,x)*9^(n-1-x) 9 故为: c(n,x)*9^(n-x)- c(n-1,x)*9^(n-1-x) 10 calc[n][x]= c(n,x)*9^(n-x) 11 dp[n][x]= c(n,x)*9^(n-x)- c(n-1,x)*9^(n-1-x) 12 dp[n][x]: n位数中有x个三的情况数目 13 14 15 方法二: 16 递推 17 18 19 */ 20 21 /* 22 算法优化后面再看,先把基础功能实现 23 */ 24 #include <iostream> 25 #define Max 10 26 using namespace std; 27 int dp[Max];//n位数中有x个三的情况数目 28 29 30 //求c(n,x) 31 int combination(int n,int x){ 32 /* 33 c(5,3)=(5*4*3)/(3*2*1) 34 */ 35 int ans=1; 36 if(n<x) return 0; 37 else if(n==x) return 1; 38 else{ 39 for(int i=n,j=1;j<=x;j++,i--){ 40 ans=ans*i/j;//这样一定能除尽 41 } 42 } 43 return ans; 44 } 45 46 //计算c(n,x)*9^(n-x) 47 int calcTimes(int n,int x){ 48 int ans=combination(n,x); 49 for(int i=1;i<=n-x;i++){ 50 ans*=9; 51 } 52 return ans; 53 } 54 55 //dp操作,没做初始化,因为全局变量都是0, 56 void dpOperation(int n){ 57 for(int i=0;i<=n;i++){ 58 if(n==1){//一位数的话,第一位可以是0 59 dp[i]=calcTimes(n,i); 60 } 61 else if(n>1){ 62 dp[i]=calcTimes(n,i)-calcTimes(n-1,i); 63 } 64 } 65 66 // for(int i=1;i<=n;i++){//计算1-n位数的情况 67 // for(int j=0;j<=i;j++){//计算i位数有j个3的情况 68 // 69 // } 70 // } 71 } 72 73 //打印dp数组 74 void print(int n){ 75 for(int i=0;i<=n;i++){ 76 cout<<n<<"位数中有"<<i<<"个3的数目:"<<dp[i]<<" "<<endl; 77 } 78 cout<<endl; 79 } 80 81 //计算偶数个3 82 int even3(int n){ 83 int ans=0; 84 for(int i=0;i<=n;i++){ 85 if(i%2==0){ 86 ans+=dp[i]; 87 } 88 } 89 return ans; 90 } 91 92 93 int main(){ 94 int n=6; 95 //int ans=combination(10,7); 96 //int ans=calcTimes(2,2); 97 //cout<<ans<<endl; 98 dpOperation(n);//dp操作,没做初始化,因为全局变量都是0, 99 //cout<<calcTimes(n,0)<<" "<<calcTimes(n-1,0)<<endl; 100 print(n);//打印dp数组 101 int ans=even3(n);//计算偶数个3 102 cout<<n<<"位数中有偶数个3的数目:"<<ans<<endl; 103 return 0; 104 }
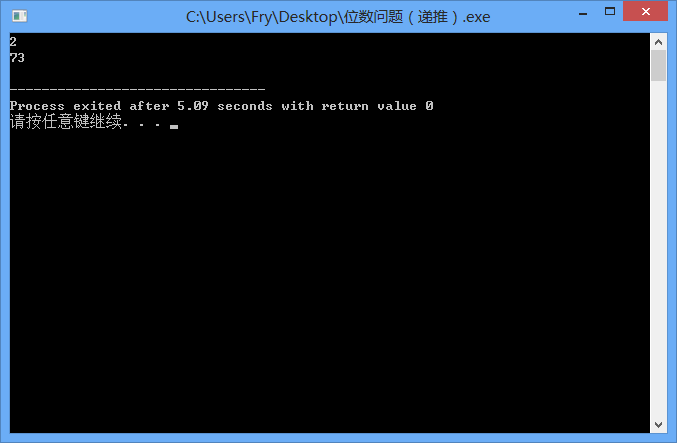
方法二、递推
1 /* 2 位数问题 : 3 在所有的n位数中,有多少个数中有偶数个数字3? 4 5 方法一: 6 排列组合 7 n位数中有x个三的情况为:c(n,x)*9^(n-x) 8 还要减去首位为0的情况:c(n-1,x)*9^(n-1-x) 9 故为: c(n,x)*9^(n-x)- c(n-1,x)*9^(n-1-x) 10 calc[n][x]= c(n,x)*9^(n-x) 11 dp[n][x]= c(n,x)*9^(n-x)- c(n-1,x)*9^(n-1-x) 12 dp[n][x]: n位数中有x个三的情况数目 13 14 15 方法二: 16 递推 17 这种题目一般都是从i-1位推导第i位,就是看第n位取不取3 18 19 f[i][0]表示前i位取偶数个3有几种情况 20 f[i][1]表示前i位取奇数个3有几种情况 21 则状态转移方程为: 22 f[i][0]=f[i-1][0]*9+f[i-1][1] 23 f[i][1]=f[i-1][1]*9+f[i-1][0] 24 边界条件:f[1][1]=1 f[1][0]=9 25 其实可以看做是取完最后一位取第一位,而0不能做第一位,所以到n的时候,是*8 26 27 28 */ 29 30 /* 31 算法优化后面再看,先把基础功能实现 32 */ 33 #include <iostream> 34 using namespace std; 35 int main(){ 36 int n; 37 int f[1005][2]={0}; 38 cin>>n; 39 f[1][1]=1; 40 f[1][0]=9; 41 for(int i=2;i<=n;i++){ 42 int x=f[1][0]; 43 if(i==n) x--;//其实可以看做是取完最后一位取第一位,而0不能做第一位,所以到n的时候,是*8 44 f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345; 45 f[i][1]=(f[i-1][1]*x+f[i-1][0])%12345; 46 } 47 cout<<f[n][0]<<endl; 48 return 0; 49 }