P1282 多米诺骨牌

P1282 多米诺骨牌

题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的

上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。例如在图8-1中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

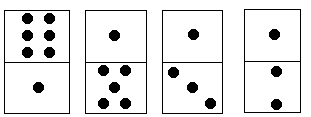
对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入输出格式

输入格式：

输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式：

输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例

输入样例#1：

4
6 1
1 5
1 3
1 2

输出样例#1：

1

 

分析：

参照洛谷题解

 

这种题目方法应该都是大同小异。

考虑一个背包，

显然如果我们直接设dp[i]表示前i个使差值最小所需的最少翻转次数，是具有后效性的。

所以我们将直接求最值，改为求某个值是否可行，这种求最值转变为求可行性的思想是非常实用的。

我们设dp[i][j]表示前i个数字通过某种旋转方式使得差值为j（不带绝对值）所需的最少翻转次数，那么我们最终dp结束后只需找到绝对值最小的非正无穷的dp值，输出即可。

考虑具体的dp过程（个人采用刷表法，填表法方程类似）：

dp[i+1][j+b[i]-a[i]]=min(dp[i][j]+1)//翻转

dp[i+1][j+a[i]-b[i]]=min(dp[i][j])//不翻转

初始化：dp[1][b[1]-a[1]]=1,dp[1][a[1]-b[1]]=0.

对于讨论中出现的极端数据，一定要把初始化方程按顺序（即=1的在上面，=0的在下面,这样的话如果a[1]=b[1]那么0就会直接覆盖上面的1）写就行了。

又因为Cpp语言中数组没有负的下标，所以还要数组平移一下。P党可以偷笑了。

至于背包不能加滚动数组的说法纯属che，dan，只是一些伪dalao的会而已。

滚动数组的方法具体可见代码。

参考代码：

#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
template<class T>void ChkMin(T &a,T b){if (b<a)a=b;}
const int INF=0x3f3f3f3f;
const int N=1010;
int dp[2][20*N],a[N],b[N];//数组使劲开，我就是开小了，先是9，然后73，然后91，最后AC = =
int n;
int main(){
    scanf("%d",&n);
    int tot=0;
    for (int i=1;i<=n;i++){
        scanf("%d %d",&a[i],&b[i]);
        tot+=abs(a[i]-b[i]);
    }
    memset(dp,0x3f,sizeof(dp));
    dp[1][2*tot-a[1]+b[1]]=1;
    dp[1][2*tot+a[1]-b[1]]=0;
    for (int i=1;i<n;i++){
        int cur=i&1,nxt=cur^1;
        memset(dp[nxt],0x3f,sizeof(dp[nxt]));
        for (int j=tot;j<=3*tot;j++)
            if (dp[cur][j]<INF){
                ChkMin(dp[nxt][j+b[i+1]-a[i+1]],dp[cur][j]+1);
                ChkMin(dp[nxt][j+a[i+1]-b[i+1]],dp[cur][j]);
            }
    }
    for (int i=2*tot;i<=3*tot;i++)
        if (dp[n&1][i]!=INF || dp[n&1][4*tot-i]!=INF){
            printf("%d",min(dp[n&1][i],dp[n&1][4*tot-i]));
            break;
        }
    return 0;
}

遇见这种直接背包。

背包的本质是什么？？？

是每一个物品或动作对所有当前状态的更新。

本题就是如此，翻一次就把原来的加的差值颠倒。

并且，本题强制必须要用每一个动作，所以就必须（即+a-b或+b-a）从前面一个状态+改变量去更新

因为改变量有正有负，所以不好降一维，

其实可以用滚动数组，但为了偷懒 (^_^），就用了二维的 (^_^）

小心负数下标数组越界！！！！！

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int a[1005],b[1005];
int f[1005][12001];
const int N=5000;
int main()
{
    int n,i,j,ans,dis;
    scanf("%d",&n);
    for(i=1;i<=n;i++)
        scanf("%d%d",&a[i],&b[i]);
    memset(f,0x7F,sizeof(f));
    f[0][0+N]=0;
//核心代码开始
    for(i=1;i<=n;i++)
        for(j=-5000;j<=5000;j++)
        {
            dis=a[i]-b[i];
            f[i][j+N]=min(f[i-1][j-dis+N],f[i-1][j+dis+N]+1);
        }
//核心代码结束
    for(i=0;i<=5000;i++)
    {
        ans=min(f[n][i+N],f[n][-i+N]);
        if(ans<=1000)
        {
            printf("%d
",ans);
            break;
        }
    }
    return 0;
}